РГР / Контрольная работа по ТАУ

14

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Контрольная работа №1

по дисциплине: Теория автоматического управления

ВАРИАНТ № 4

Выполнил: студент 2-го курса

Золотовский Денис Васильевич

Шифр: 04−ЭПу−934

Проверил: Рычков Владимир Викентьевич

Киров

2005

Типовые динамические звенья САУ

Рис. 1.1

Дано:

Ом; Ом;

с; с; с;

; ; С = 0,001Ф; L = 10Гн.

Задача 1.1

1. Вычертить электрическую принципиальную схему и привести числовые параметры схемы;

2. записать дифференциальное уравнение зависимостей между током и напряжением цепей схемы и привести их операторное изображение по Лапласу при нулевых начальных условиях.

Решение: 1)Запишем уравнение зависимостей между током и напряжением на основании и 1−го и 2−го закона Кирхгофа;

перейдём к операторному изображению:

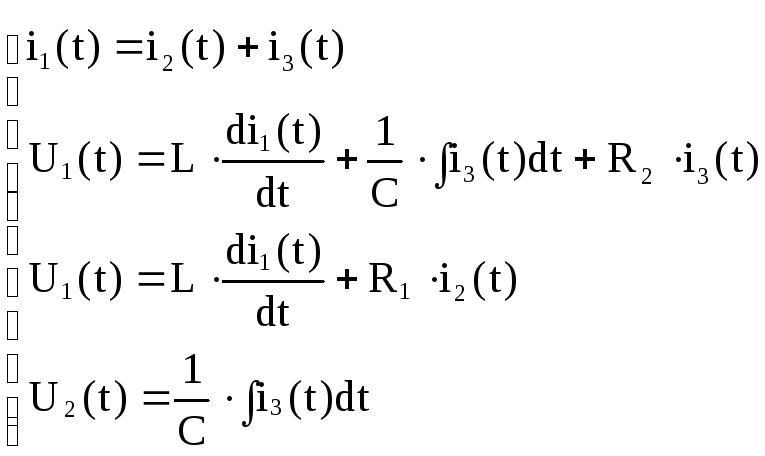
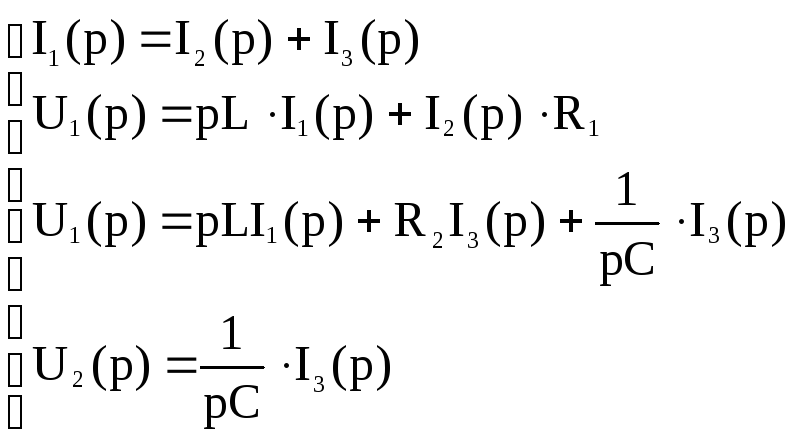
2)Решим полученную систему уравнений относительно выходного и входного воздействия:

Имеем в виду, что для точек a и b – одно напряжение. Тогда

;

;

;

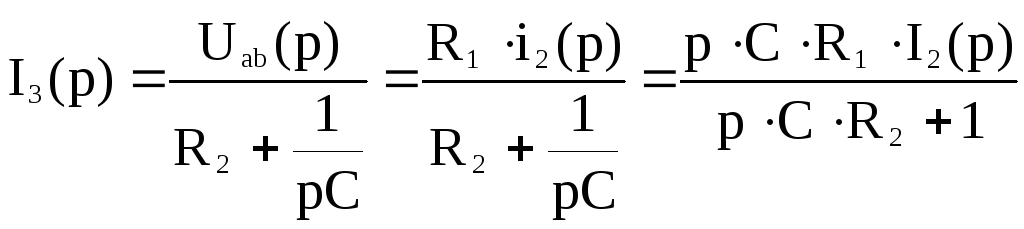Отсюда получим выражение:

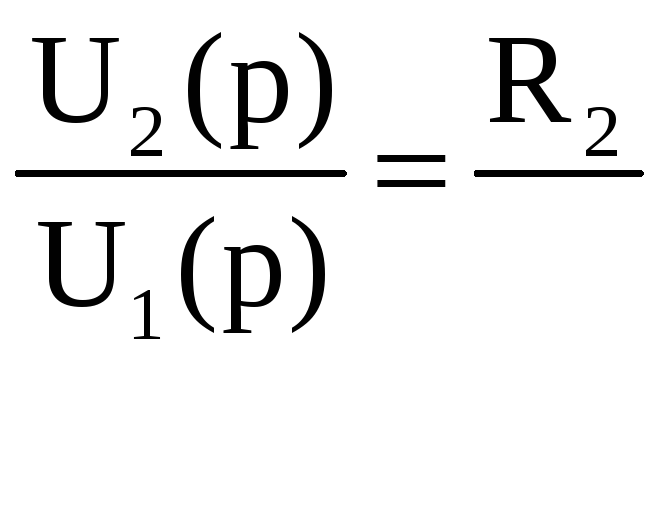
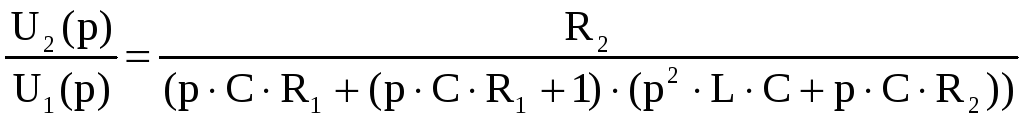
3. Решим характеристическое уравнение данной передаточной функции и определим его корни:

4. Найдём передаточную функцию W(p).

Передаточную функцию данной схемы можно найти как произведение передаточных функций первого и второго звена:

Найдём передаточную функцию первого звена:

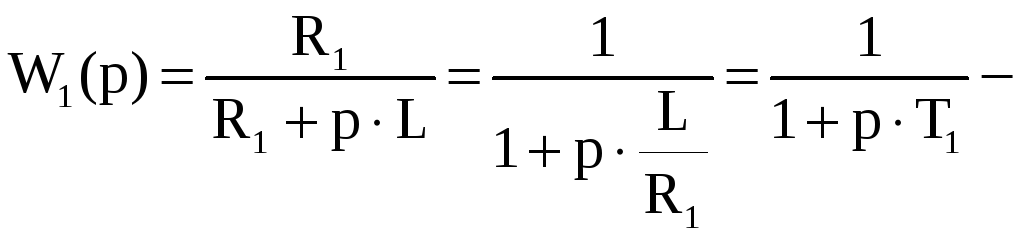это апериодическое звено, где

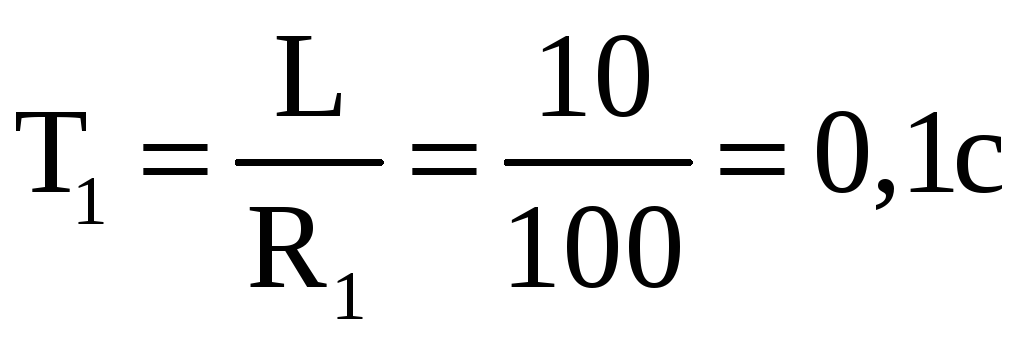
Найдём передаточную функцию второго звена:

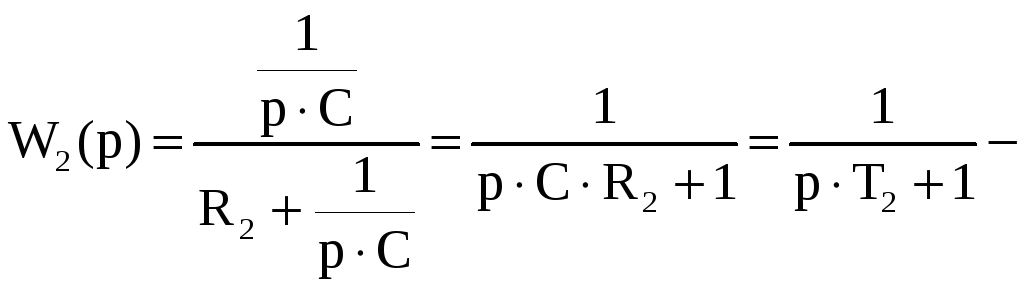это апериодическое звено, где

Тогда получим:

=

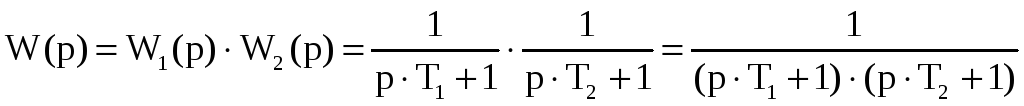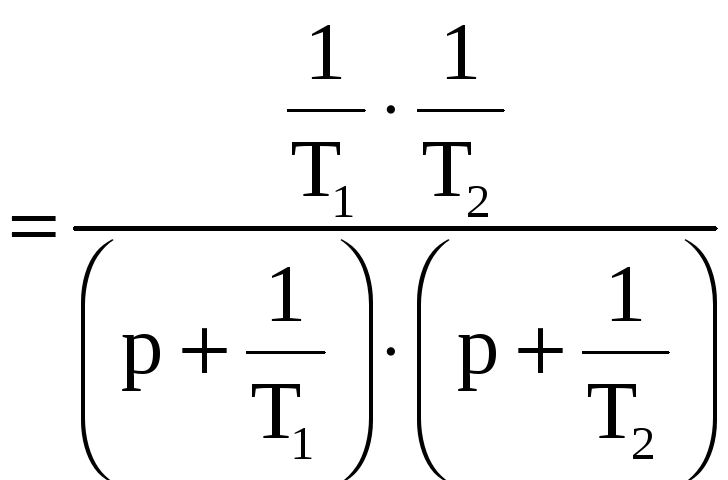
З

арисуем структурную схему:

В данной структурной схеме оба звена являются инерционными.

5) Найдём переходную функцию c помощью операторного метода при единичном ступенчатом воздействии на входе :

.

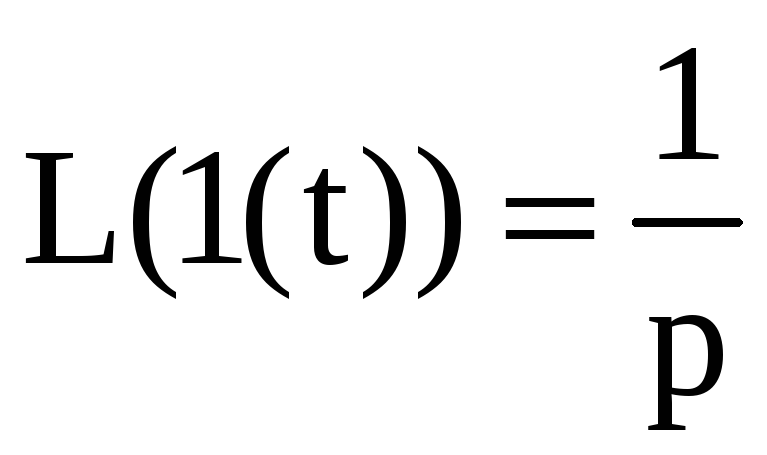Тогда переходная функция вычисляется по формуле:

+

++

+

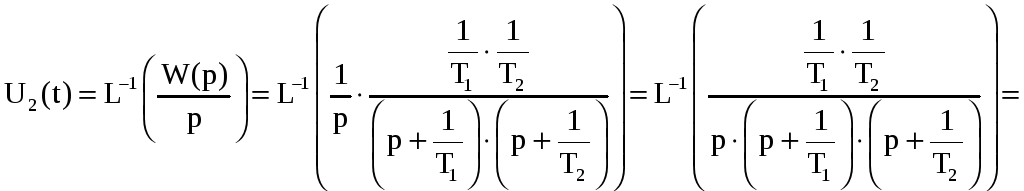
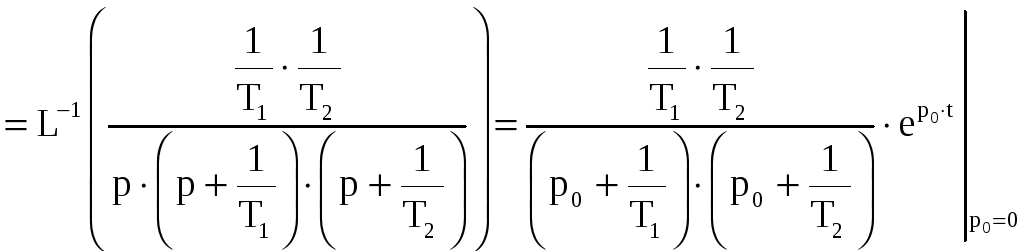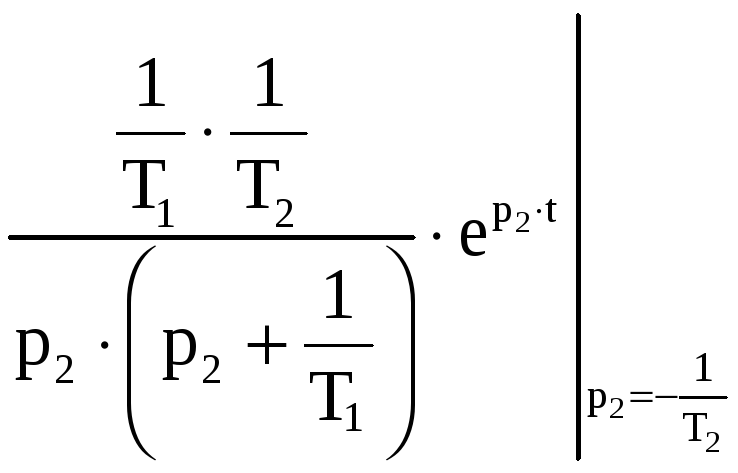
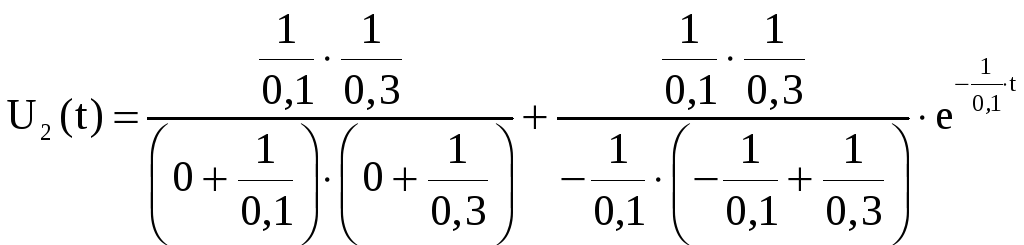Построим график переходной функции

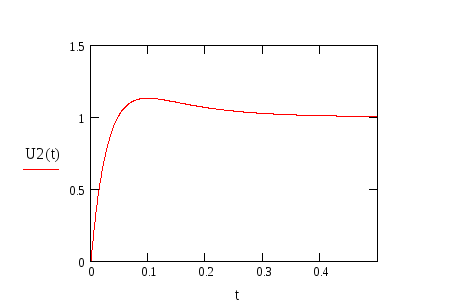
4. Найдём аналитические выражения для комплексного коэффициента передачи 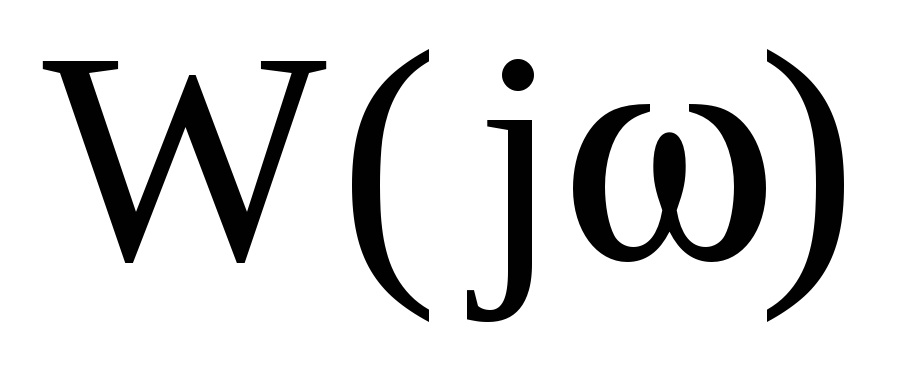. Преобразуем передаточную функцию:

.

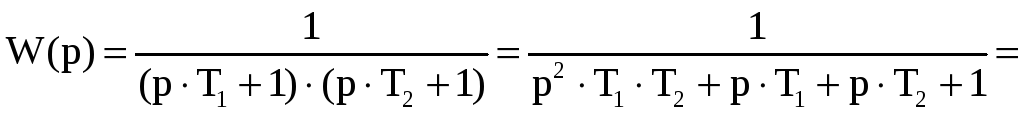
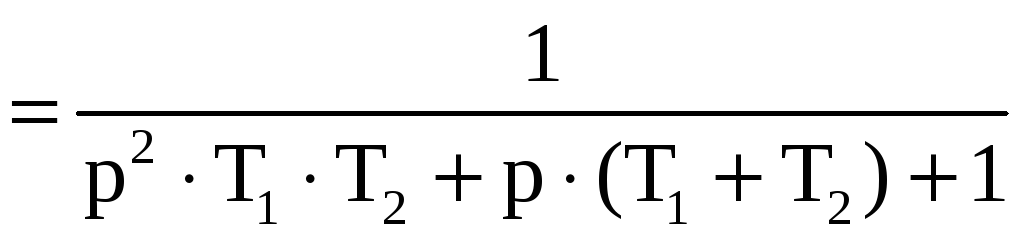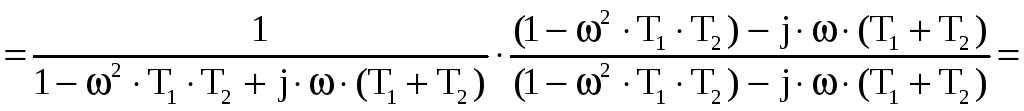
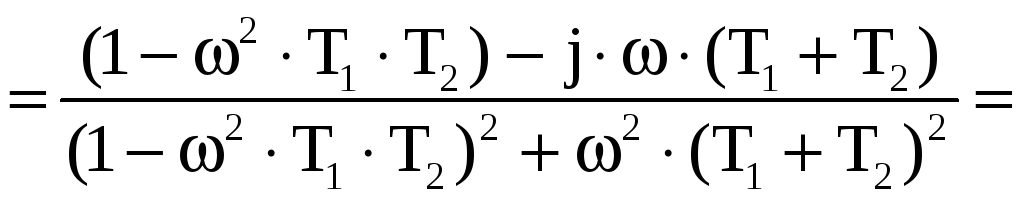
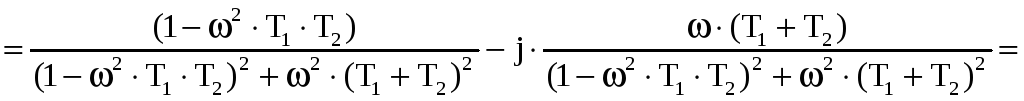
Передаточная функция в аналитической форме представляется в следующем виде:

амплитудно-частотная характеристика (АЧХ):

;

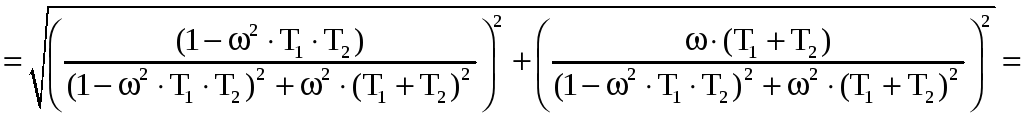
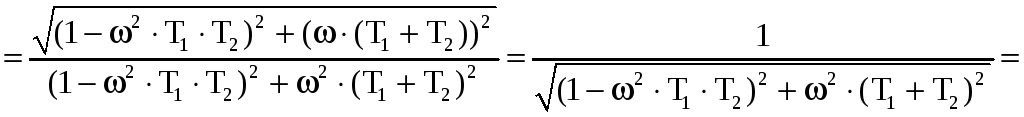
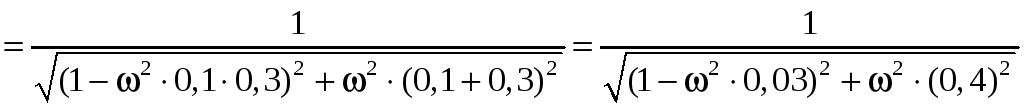фазо-частотная характеристика (ФЧХ):

;

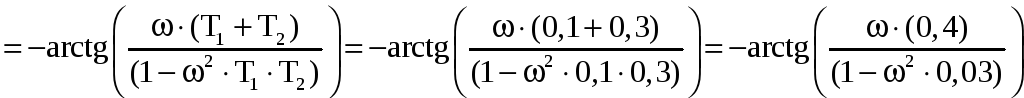логарифмическая амплитудно-частотная характеристика (ЛАЧХ):

;

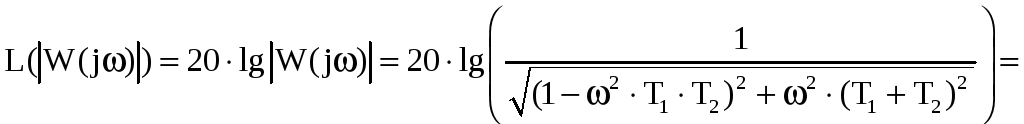
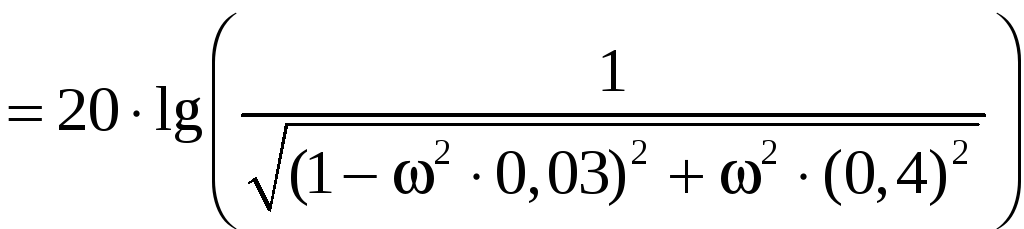логарифмическая фазочастотная характеристика (ЛФЧХ):

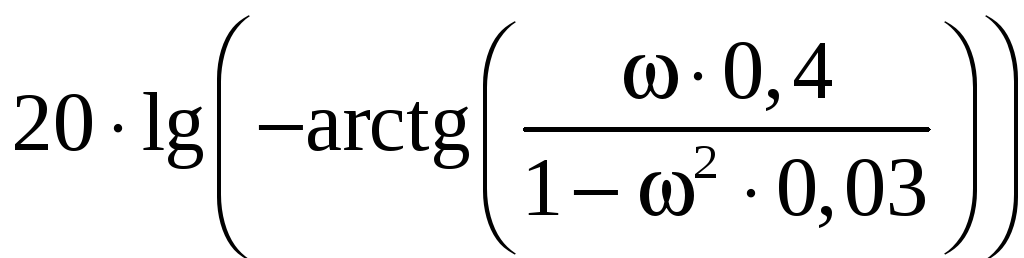
4. Построим на графике точные и асимптотические ЛАЧХ и ЛФЧХ.

ЛАЧХ системы:

При построении ЛАЧХ откладываем по оси ординат модуль частотной передаточной функции, по оси абсцисс – угловую частоту в логарифмическом масштабе.

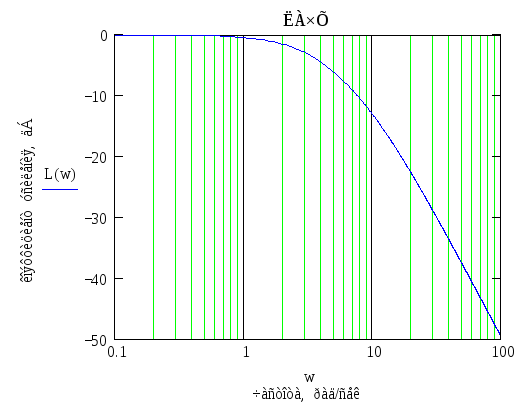
Логарифмическая фазочастотная характеристика (ЛФЧХ) строится в виде зависимости от lg. Фазу откладывают в радианах. Построим график ЛФЧХ:

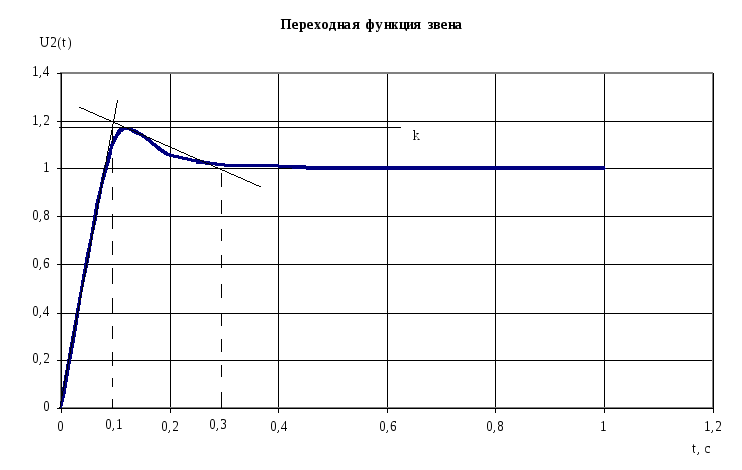
8. Построим приближённую переходную функцию по ЛАЧХ системы. Для этого выполним следующее:

Найдём частоты сопряжения:

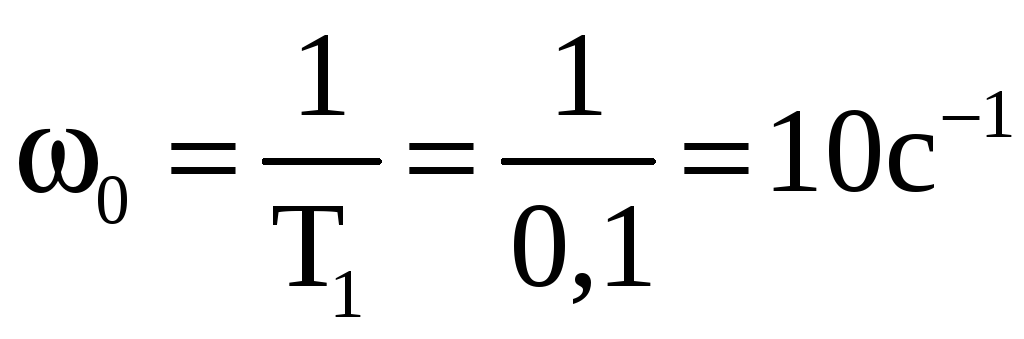
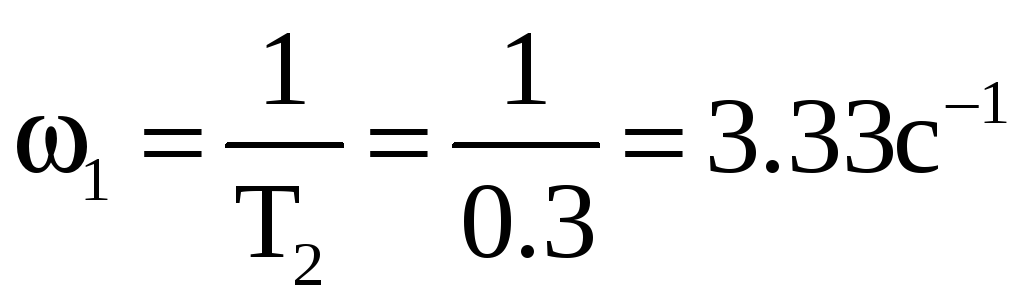
Определим начальное значение переходного процесса:

Определим установившееся значение переходного процесса:

Определим максимально возможное значение переходного процесса:

Из начала координат на прямую k отложим подкасательную и построим экспоненту, соответствующую кривой нарастания. Затем отложим подкасательную и построим экспоненту, соответствующую спадающему участку кривой переходного процесса.

Результирующая кривая получается путём плавного перехода с нарастающего участка на экспоненту, соответствующую спадающему участку.

Библиография:

1. Теория автоматического управления, под ред. Соломенцева,

Москва, «Высшая школа», 2000г.

2. Теория автоматического управления, А.А.Ерофеев, Санкт-Петербург,

«Политехника», 2001г.

3. Техническая кибернетика, Э.И.Гитис, Г.А.Данилович,

В.И.Самойленко, Москва, 1968г.

4. Теория систем автоматического управления, В. А. Бесекерский, Е. П.

Попов, Санкт-Петербург, издательство «Профессия», 2003г.