РГР / raschetno_graficheskaya_rabota (2)

7

Вариант №6

Дано:

Коэффициенты полиномов а₀ = 6; а₁ = 3; а₂ = 2; b₀ = 11; b₁ = 6.

Время запаздывания τ = 6 с.

Передаточная функция объекта

[Па/К]

Требуется:

1. Построить по известной передаточной функции АФЧХ, АЧХ, ФЧХ.

2. Построить АФЧХ, АЧХ, ФЧХ для данного звена с учетом запаздывания.

3. Определить переходную функцию.

4. Найти оригиналы передаточной и переходной функции, построить их графики.

5. Оценить как влияет запаздывание на характеристики звена.

Решение.

Представим передаточную функцию в частотном виде. Для этого осуществим подстановку в исходную функцию выражения s = j·ω

.

Выразим передаточную функцию в виде

, (1)

где ;

.

На основе полученного выражения (1) построим амплитудную фазо-частотную характеристику (АФЧХ) объекта при изменении частоты от 0 до +∞

Рисунок 1 – АФЧХ объекта

Определим амплитудно-частотную характеристику (АЧХ) объекта по формуле

или

.

На основе полученного выражения построим АЧХ объекта при изменении частоты от 0 до +∞

Рисунок 2 – АЧХ объекта

Определим фазо-частотную характеристику (ФЧХ) объекта по формуле

или

.

На основе полученного выражения построим ФЧХ объекта при изменении частоты от 0 до +∞

Рисунок 3 – ФЧХ объекта

Определим переходную функцию в операторном виде по известной передаточной функции

.

Найдем оригинал передаточной функции ω(t), которая называется весовой функцией. Для этого применим формулу

, (2)

где B(s) = 6·s+11 ;

A’(s) = (2·s² + 3·s + 6)^’ = 4·s + 3 ;

s_i – i-ый корень характеристичекого полинома.

Найдем корни характеристического полинома

A(s) = 2·s² + 3·s + 6 = 0,

D = 3² - 4·2·6 = -39,

, . (3)

Далее по формуле (2) получим

.

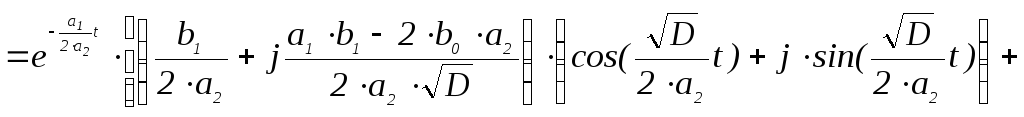
Построим график весовой функции

Рисунок 4 – График весовой функции

Найдем оригинал переходной функции h(t). Для этого применим формулу

, (4)

где B(s) = 6·s+11 ;

A’(s) = (2·s² + 3·s + 6)^’ = 4·s + 3 ;

s_i – i-ый корень характеристичекого полинома.

Корни характеристического полинома определяются по формуле (3). Далее по формуле (4) получим

.

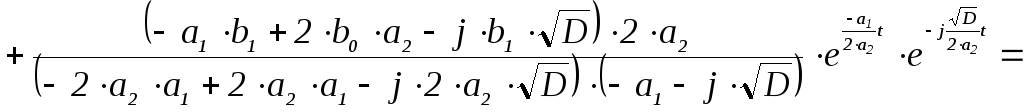
Построим график переходного процесса

Рисунок 5 – График переходной функции