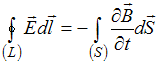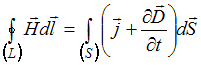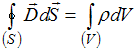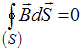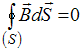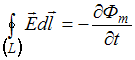- •Контрольное тестирование по физике
- •Де n1. Механика.
- •1. Кинематика поступательного и вращательного движения
- •2. Динамика поступательного движения
- •3. Динамика вращательного движения
- •4. Работа. Энергия
- •5. Законы сохранения в механике
- •6. Элементы специальной теории относительности
- •Де n2. Молекулярная (статистическая) физика и термодинамика.
- •7. Средняя энергия молекул
- •8. Распределения Максвелла и Больцмана
- •9. Первое начало термодинамики. Работа при изопроцессах
- •10. Второе начало термодинамики. Энтропия
- •Де n3. Электричество и магнетизм.
- •11. Электростатическое поле в вакууме
- •12. Законы постоянного тока
- •13. Магнитостатика
- •14. Электрические и магнитные свойства вещества
- •15. Явление электромагнитной индукции
- •16. Уравнения Максвелла
- •Де n4. Механические и электромагнитные колебания и волны.
- •17. Свободные и вынужденные колебания
- •18. Сложение гармонических колебаний
- •19. Волны. Уравнение волны
- •20. Энергия волны. Перенос энергии волной
- •Де n5. Волновая и квантовая оптика.
- •21. Интерференция и дифракция света
- •22. Поляризация и дисперсия света
- •23. Эффект Комптона. Световое давление
- •24. Тепловое излучение. Фотоэффект
- •Де n6. Квантовая физика и физика атома.
- •25. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •26. Спектр атома водорода. Правило отбора
- •27. Уравнение Шредингера (общие свойства)
- •28. Уравнение Шредингера (конкретные ситуации)
- •Де n7. Элементы ядерной физики и физики элементарных частиц.
- •29. Фундаментальные взаимодействия
- •30. Ядро. Элементарные частицы
- •31. Ядерные реакции.
- •32.Законы сохранения в ядерных реакциях
16. Уравнения Максвелла
Уравнения Максвелла
являются основными законами классической
макроскопической электродинамики,
сформулированными на основе обобщения
важнейших законов электростатики и
электромагнетизма. Эти уравнения в
интегральной форме имеют
вид:
1).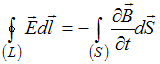 ;
2).
;
2).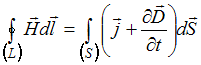 ;
3).
;
3).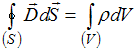 ;
4).
;
4).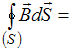 0.
Третье
уравнение Максвелла является обобщением …
0.
Третье
уравнение Максвелла является обобщением …
|
|
|
|
теоремы Остроградского – Гаусса для электростатического поля в среде |
|
|
|
|
закона электромагнитной индукции |
|
|
|
|
закона полного тока в среде |
|
|
|
|
теоремы Остроградского – Гаусса для магнитного поля |
Решение: Третье уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Полная система
уравнений Максвелла для электромагнитного
поля в интегральной форме имеет
вид:
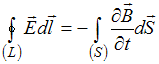 ,
,
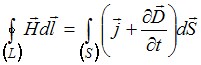 ,
,
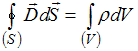 ,
,
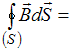 0.
Следующая
система уравнений:
0.
Следующая
система уравнений:
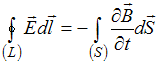 ,
,
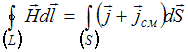 ,
,
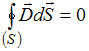 ,
,
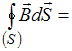 0
–
справедлива для …
0
–
справедлива для …
|
|
|
|
электромагнитного поля в отсутствие свободных зарядов |
|
|
|
|
электромагнитного поля в отсутствие свободных зарядов и токов проводимости |
|
|
|
|
электромагнитного поля в отсутствие токов проводимости |
|
|
|
|
стационарных электрических и магнитных полей |
Решение:
Вторая
система уравнений отличается от первой
системы своими вторым и третьим
уравнениями. Во втором уравнении иначе
записано подынтегральное выражение,
но
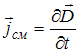 .
В третьем уравнении отсутствует плотность
.
В третьем уравнении отсутствует плотность
![]() свободных
зарядов. Следовательно, рассматриваемая
система справедлива для электромагнитного
поля в отсутствие свободных зарядов.
свободных
зарядов. Следовательно, рассматриваемая
система справедлива для электромагнитного
поля в отсутствие свободных зарядов.
22. Полная система уравнений Максвелла
для электромагнитного поля в интегральной
форме имеет вид:
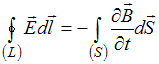 ,
,
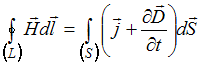
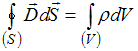
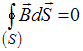 Следующая система уравнений:
Следующая система уравнений:
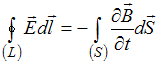
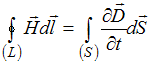
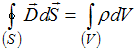
 справедлива для …
справедлива для …
|
|
электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости |
|
|
электромагнитного поля в отсутствие заряженных тел и токов проводимости |
|
|
стационарных электрических и магнитных полей в отсутствие токов проводимости |
|
|
электромагнитного поля при наличии заряженных тел и токов проводимости |
Решение:
Вторая система отличается
от первой системы своим вторым уравнением,
а именно: отсутствует в подынтегральном
выражении плотность тока проводимости
![]() . Это означает, что источником
вихревого магнитного поля является
только переменное электрическое поле.
Таким образом, рассматриваемая система
справедлива для переменного
электромагнитного поля при наличии
заряженных тел и в отсутствие токов
проводимости.
. Это означает, что источником
вихревого магнитного поля является
только переменное электрическое поле.
Таким образом, рассматриваемая система
справедлива для переменного
электромагнитного поля при наличии
заряженных тел и в отсутствие токов
проводимости.
23. Утверждение «В любой точке пространства изменяющееся со временем магнитное поле порождает вихревое электрическое поле» раскрывает физический смысл уравнения …
|
|
|
|
|
|
|
|
|
Решение: Из уравнения
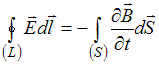 следует,
что изменяющееся со временем магнитное
поле (для которого
следует,
что изменяющееся со временем магнитное
поле (для которого
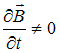 ),
является источником вихревого
электрического поля, отличительная
особенность которого – отличие от нуля
циркуляции вектора напряженности поля.
),
является источником вихревого
электрического поля, отличительная
особенность которого – отличие от нуля
циркуляции вектора напряженности поля.
24. Следующее утверждение «Никаких источников магнитного поля, подобных электрическим зарядам (по аналогии их называют магнитными зарядами) в природе не существует» – является следствием уравнения …
|
|
|
|
|
|
|
|
|
Решение: Утверждение « Никаких
источников магнитного поля, подобных
электрическим зарядам (по аналогии их
называют магнитными зарядами) в природе
не существует» является следствием
уравнения
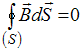 .
Это уравнение Максвелла – обобщение
теоремы Гаусса на любое магнитное поле.
.
Это уравнение Максвелла – обобщение
теоремы Гаусса на любое магнитное поле.
25. Полная система уравнений Максвелла
для электромагнитного поля в интегральной
форме имеет вид:
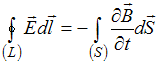

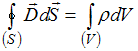
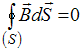 Система
распадается на две группы независимых
уравнений:
Система
распадается на две группы независимых
уравнений:
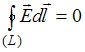 ,
,
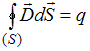 ,
,
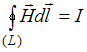
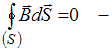 ,при
условии, что …
,при
условии, что …
|
|
|
|
|
|
|
|
|
Решение: Из сопоставления второй
системы с первой следует, что
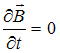 и
и
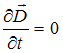 ,
то есть магнитное и электрическое поля
стационарны:
,
то есть магнитное и электрическое поля
стационарны:
![]() и
и
![]() (а
следовательно, и
(а
следовательно, и
![]() ).
В этом случае электрическое и магнитное
поля независимы друг от друга.
).
В этом случае электрическое и магнитное
поля независимы друг от друга.