- •Контрольное тестирование по физике
- •Де n1. Механика.
- •1. Кинематика поступательного и вращательного движения
- •2. Динамика поступательного движения
- •3. Динамика вращательного движения
- •4. Работа. Энергия
- •5. Законы сохранения в механике
- •6. Элементы специальной теории относительности
- •Де n2. Молекулярная (статистическая) физика и термодинамика.
- •7. Средняя энергия молекул
- •8. Распределения Максвелла и Больцмана
- •9. Первое начало термодинамики. Работа при изопроцессах
- •10. Второе начало термодинамики. Энтропия
- •Де n3. Электричество и магнетизм.
- •11. Электростатическое поле в вакууме
- •12. Законы постоянного тока
- •13. Магнитостатика
- •14. Электрические и магнитные свойства вещества
- •15. Явление электромагнитной индукции
- •16. Уравнения Максвелла
- •Де n4. Механические и электромагнитные колебания и волны.
- •17. Свободные и вынужденные колебания
- •18. Сложение гармонических колебаний
- •19. Волны. Уравнение волны
- •20. Энергия волны. Перенос энергии волной
- •Де n5. Волновая и квантовая оптика.
- •21. Интерференция и дифракция света
- •22. Поляризация и дисперсия света
- •23. Эффект Комптона. Световое давление
- •24. Тепловое излучение. Фотоэффект
- •Де n6. Квантовая физика и физика атома.
- •25. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •26. Спектр атома водорода. Правило отбора
- •27. Уравнение Шредингера (общие свойства)
- •28. Уравнение Шредингера (конкретные ситуации)
- •Де n7. Элементы ядерной физики и физики элементарных частиц.
- •29. Фундаментальные взаимодействия
- •30. Ядро. Элементарные частицы
- •31. Ядерные реакции.
- •32.Законы сохранения в ядерных реакциях
15. Явление электромагнитной индукции
Проводящая рамка
вращается с постоянной угловой скоростью
в однородном магнитном поле вокруг оси,
лежащей в плоскости рамки и перпендикулярной
вектору индукции
![]() (см.
рис.). На рисунке также представлен
график зависимости от времени потока
вектора магнитной индукции, пронизывающего
рамку.
(см.
рис.). На рисунке также представлен
график зависимости от времени потока
вектора магнитной индукции, пронизывающего
рамку.
 Если
максимальное значение магнитного потока
Если
максимальное значение магнитного потока
![]() мВб,
сопротивление рамки
мВб,
сопротивление рамки
![]() Ом,
а время измерялось в секундах, то закон
изменения со временем силы индукционного
тока имеет вид …
Ом,
а время измерялось в секундах, то закон
изменения со временем силы индукционного
тока имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Сила
индукционного тока
![]() ,
где
,
где
![]() –
ЭДС индукции, R
– сопротивление рамки. В соответствии
с законом Фарадея для электромагнитной
индукции
–
ЭДС индукции, R
– сопротивление рамки. В соответствии
с законом Фарадея для электромагнитной
индукции
![]() .
Чтобы найти закон изменения ЭДС индукции
со временем, необходимо знать зависимость
от времени магнитного потока, пронизывающего
рамку. Из приведенного графика следует,
что
.
Чтобы найти закон изменения ЭДС индукции
со временем, необходимо знать зависимость
от времени магнитного потока, пронизывающего
рамку. Из приведенного графика следует,
что
![]() ,
поскольку
,
поскольку
![]() Тогда
Тогда
![]() ,
а
,
а
![]()
1 8.
По параллельным металлическим проводникам,
расположенным в однородном магнитном
поле, с постоянной скоростью перемещается
проводящая перемычка (см. рис.). Если
сопротивлением перемычки и направляющих
можно пренебречь, то зависимость
индукционного тока от времени можно
представить графиком …
8.
По параллельным металлическим проводникам,
расположенным в однородном магнитном
поле, с постоянной скоростью перемещается
проводящая перемычка (см. рис.). Если
сопротивлением перемычки и направляющих
можно пренебречь, то зависимость
индукционного тока от времени можно
представить графиком …
|
|
|
|
|
|
|
|
|
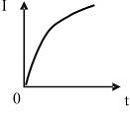
Решение: При движении проводящей
перемычки в магнитном поле в ней возникает
ЭДС индукции и индукционный ток. Согласно
закону Ома для замкнутой цепи,
![]() ,
а ЭДС индукции определяется из закона
Фарадея:
,
а ЭДС индукции определяется из закона
Фарадея:
![]() ,
где
,
где
![]() –
магнитный поток сквозь поверхность,
прочерчиваемую перемычкой при ее
движении за промежуток времени
–
магнитный поток сквозь поверхность,
прочерчиваемую перемычкой при ее
движении за промежуток времени
![]() .
Учитывая, что
.
Учитывая, что
![]() (поскольку
индукция
(поскольку
индукция![]() магнитного
поля перпендикулярна плоскости, в
которой происходит движение проводника),
а
магнитного
поля перпендикулярна плоскости, в
которой происходит движение проводника),
а
![]() ,
где
,
где
![]() –
длина перемычки, получаем:
–
длина перемычки, получаем:
![]() .
Тогда
.
Тогда
![]() ,
а величина индукционного тока
,
а величина индукционного тока
![]() .
Поскольку
.
Поскольку
![]() ,
то и индукционный ток не изменяется со
временем.
,
то и индукционный ток не изменяется со
временем.
1 9.
Прямоугольная проволочная рамка
расположена в одной плоскости с
прямолинейным длинным проводником, по
которому течет ток I. Индукционный ток
в рамке будет направлен по часовой
стрелке при ее
9.
Прямоугольная проволочная рамка
расположена в одной плоскости с
прямолинейным длинным проводником, по
которому течет ток I. Индукционный ток
в рамке будет направлен по часовой
стрелке при ее
|
|
поступательном перемещении в положительном направлении оси OX |
|
|
поступательном перемещении в отрицательном направлении оси OX |
|
|
поступательном перемещении в положительном направлении оси OY |
|
|
вращении вокруг оси, совпадающей с длинным проводником |
Решение: При изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в нем возникает индукционный ток, направление которого можно найти по правилу Ленца. В данном случае в прямоугольной проволочной рамке индукционный ток будет протекать по часовой стрелке при ее поступательном перемещении в положительном направлении оси OX.
|
20. Проводящая рамка
вращается с постоянной угловой
скоростью в однородном магнитном поле
вокруг оси, лежащей в плоскости рамки
и перпендикулярной вектору индукции
|
|
|
|
|
|
|
|
|
|
|
Решение: В соответствии с законом
Фарадея для электромагнитной индукции
![]() .
Чтобы найти закон изменения ЭДС индукции
со временем, необходимо знать зависимость
от времени магнитного потока, пронизывающего
рамку. Из приведенного графика следует,
что
.
Чтобы найти закон изменения ЭДС индукции
со временем, необходимо знать зависимость
от времени магнитного потока, пронизывающего
рамку. Из приведенного графика следует,
что
![]() ,
поскольку Т = 4 с. Тогда
,
поскольку Т = 4 с. Тогда
![]() .
.
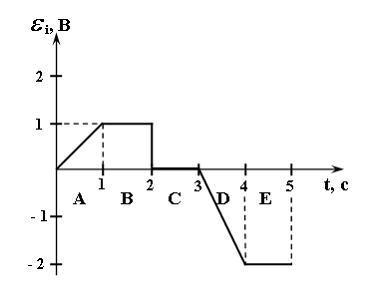
19. На рисунке представлена зависимость ЭДС индукции в контуре от времени. Магнитный поток сквозь площадку, ограниченную контуром, увеличивается со временем по линейному закону в интервале …
Решение: В соответствии с законом
Фарадея для электромагнитной индукции
электродвижущая сила индукции в замкнутом
проводящем контуре численно равна и
противоположна по знаку скорости
изменения магнитного потока сквозь
поверхность, ограниченную этим контуром:
![]() .
Следовательно, если магнитный поток
увеличивается со временем по линейному
закону, то ЭДС индукции будет равна
отрицательной постоянной величине,
что имеет место в интервале Е.
.
Следовательно, если магнитный поток
увеличивается со временем по линейному
закону, то ЭДС индукции будет равна
отрицательной постоянной величине,
что имеет место в интервале Е.
21. Проводящий плоский контур площадью
100 см2 расположен в магнитном поле
перпендикулярно линиям магнитной
индукции. Если магнитная индукция
изменяется по закону
![]() Тл,
то ЭДС индукции, возникающая в контуре
в момент времени
Тл,
то ЭДС индукции, возникающая в контуре
в момент времени
![]() (в
мВ), равна …
(в
мВ), равна …
|
|
0,12 |
|
120 |
|
1,2 |
|
12 |
Решение:
В соответствии с законом
Фарадея для электромагнитной индукции
электродвижущая сила индукции в замкнутом
проводящем контуре численно равна и
противоположна по знаку скорости
изменения магнитного потока сквозь
поверхность, ограниченную этим контуром:
![]() .
Поскольку плоскость контура перпендикулярна
линиям магнитной индукции,
.
Поскольку плоскость контура перпендикулярна
линиям магнитной индукции,
![]() ,
где S – площадь контура. Таким
образом,
,
где S – площадь контура. Таким
образом,
![]() В
= 0,12 мВ.
В
= 0,12 мВ.