
- •§ 1. Теория теплообмена (основные понятия)
- •1.1 Основные определения
- •1.2. Закон Фурье
- •1.3. Дифференциальное уравнение энергии
- •§ 2. Теплопроводность
- •2.1. Введение
- •2.2. Условия однозначности для тепловых процессов
- •2.3. Передача тепла через плоскую стенку в стационарных условиях
- •2.3.1. Граничное условие первого рода
- •2.3.2. Граничное условие третьего рода
- •2.4. Передача тепла через цилиндрическую стенку
- •2.4.1. Уравнение энергии в цилиндрических координатах
- •2.4.2. Граничное условие первого рода
- •2.4.3. Граничное условие третьего рода
- •2.5. Критический диаметр тепловой изоляции
- •§ 3. Конвекция
- •3.1. Конвективный перенос теплоты
- •3.2. Краткие сведения о газодинамике неизотермического течения
- •3.3. Дифференциальные уравнения движения газа
- •Уравнение неразрывности
- •Уравнение движения
- •§4. Элементы теории подобия
- •§7. Вынужденное движение жидкости (газа). Понятие пограничного слоя
- •7.2. Дифференциальные уравнения динамического пограничного слоя
- •7.3. Характер движения жидкости вдоль поверхности
- •§8. Теплообмен при ламинарном и турбулентном движении жидкости (газа)
- •8.1. Теплоотдача при ламинарном пограничном слое
- •8.2. Теплоотдача при турбулентном пограничном слое
- •§9. Особенности движения и теплообмена в трубах и каналах
- •9.1. Теплоотдача при вязкостном ламинарном течении жидкости в гладких трубах круглого сечения
- •9.2. Теплоотдача при турбулентном течении жидкости в трубах различного сечения
- •§10. Теплоотдача при свободном движении жидкости в большом объёме
- •10.2. Теплоотдача при свободном движении жидкости в ограниченном пространстве
- •§12. Теплообменные аппараты. Общие сведения
- •12.1. Классификация теплообменных аппаратов
2.4. Передача тепла через цилиндрическую стенку
2.4.1. Уравнение энергии в цилиндрических координатах
В реальных условиях плоских стенок с бесконечно большой площадью не существует. Как правило, задачи теплообмена сводятся к анализу теплового состояния замкнутых полостей или протяжённых каналов. Простейшим случаем является теплопередача через стенки достаточно длинной трубы. Труба обладает радиальной симметрией, и теплота передаётся только в направлении радиуса трубы. Соответственно в одномерном приближении исходное дифференциальное уравнение теплопроводности в цилиндрических координатах можно получить следующим образом.

Выделим бесконечно
малый объём газа и рассмотрим тепловой
баланс этого объёма. Изменение всех
параметров процесса по координате
![]() равно 0.
равно 0.
![]()
В отсутствии внутренних источников теплоты, теплота подведённая к системе за единицу времени может быть записана следующим образом:

Член
 изначально необходимо рассматривать
как приращение количества теплоты не
за счёт приращения угла ,
а за счёт приращения длины дуги l
по радиусу r
изначально необходимо рассматривать
как приращение количества теплоты не
за счёт приращения угла ,
а за счёт приращения длины дуги l
по радиусу r
 по аналогии с задачей теплопроводности
в декартовой системе координат.
по аналогии с задачей теплопроводности
в декартовой системе координат.
Запишем выражения для плотности теплового потока в виде:
![]() ,
,
где, согласно закону Фика:

По
закону Фика тепловой поток пропорционален
градиенту температуры по направлению.
В данном случае это дуга l
по радиусу r
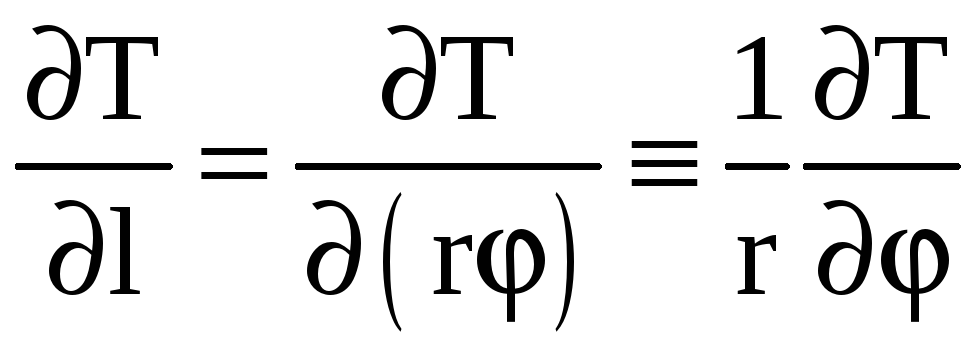
С учётом закона Фика дифференциальное уравнение теплообмена можно получить в виде:

 (6)
(6)
2.4.2. Граничное условие первого рода
В стационарных
условиях при равномерном распределении
температуры по стенкам трубы
дифференциальное уравнение теплообмена
упрощается
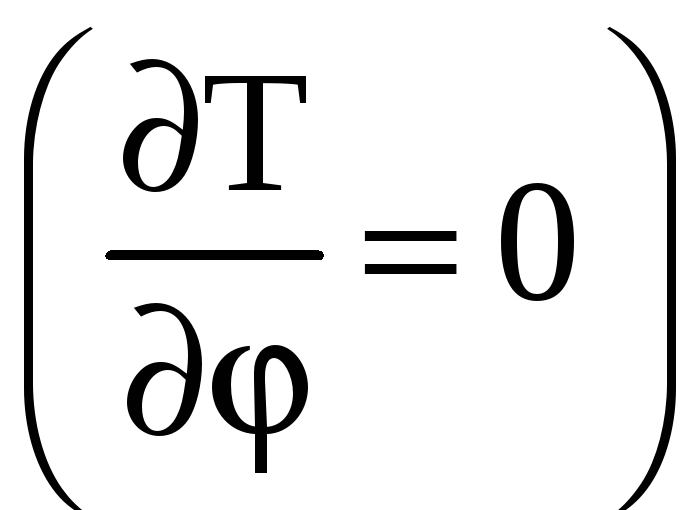 и возможно получить его точное решение.
и возможно получить его точное решение.

Таким образом, уравнение, описывающее теплопередачу через цилиндрическую стенку можно записать следующим образом:
 (7)
(7)
Введём новую
переменную
![]() ,
тогда:
,
тогда:

Константы интегрирования определим из граничных условий:


В итоге получаем следующее выражение для температуры внутри стенки трубы:
 (8)
(8)
Полный тепловой поток через изотермическую поверхность можно оценить по закону Фурье в виде:
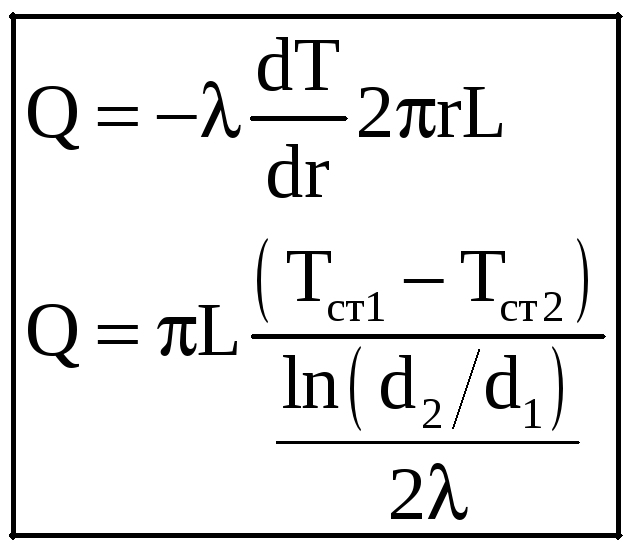 , (9)
, (9)
где L
длина трубы. Величину
 называют внутренним
термическим
сопротивлением цилиндрической стенки
или линейным внутренним
термическим
сопротивлением цилиндрической стенки,
мград/Вт.
Величина
называют внутренним
термическим
сопротивлением цилиндрической стенки
или линейным внутренним
термическим
сопротивлением цилиндрической стенки,
мград/Вт.
Величина
![]()
линейная
плотность теплового потока,
Вт/м. Тогда
с учетом выражения для ql
формулу (9) можно переписать следующим
образом
линейная
плотность теплового потока,
Вт/м. Тогда
с учетом выражения для ql
формулу (9) можно переписать следующим
образом
 (10)
(10)
Анализ теплопроводности многослойных стенок трубы приводит к следующему выражению для теплового потока, полученному из (10) с учетом аналогичного подхода, как и для плоской стенки (см. соотношение (5)).
 (11)
(11)
В случае тонкостенной конструкции, когда d2/d12 (в реальности для почти всех труб выполняется такое условие) логарифмическим профилем температуры можно пренебречь и можно использовать следующую упрощенную формулу:
![]() ,
,
где
![]()
толщина стенки, м, dср
– средний диаметр трубы, м.
толщина стенки, м, dср
– средний диаметр трубы, м.
2.4.3. Граничное условие третьего рода
Для задач теплопередачи в сложных условиях (с учетом конвекции, излучения и т.д.) применяют формулу вида:
 (12)
(12)
