Лекция 01 Ряды

ЛЕКЦИЯ 1

1. Ряды.

   2. Числовые ряды. Сходимость и сумма ряда. Необходимый признак сходимости. Знакопостоянные ряды. Достаточные признаки сходимости.

Ранее были установлены свойства и правила при суммировании конечного числа слагаемых, например: сумма не изменяется при перестановке слагаемых, производная суммы функций равна сумме их производных и т.д. Вопрос состоит в том, что в каком случае м при каких условиях эти свойства конечных сумм могут переноситься на суммы бесконечные.

1.2.1. ОПРЕДЕЛЕНИЕ РЯДА. СХОДИМОСТЬ И РАСХОДИМОСТЬ РЯДА.

Пусть дана последовательность действительных чисел

Выражение вида

(1.1)

называется числовым рядом, числа -членами ряда, - n-ым или общим членом ряда. Сумма n первых членов ряда называется n-ой частичной суммой и обозначается символом : .

Если для последовательности частичных сумм существует конечный предел S, то ряд (1.1) называется сходящимся, а число S –суммой данного ряда. В этом случае пишут: ; .

Ряд (1.1) называется расходящимся, если не существует или бесконечен. Ряд, полученный из (1.1) отбрасыванием первых его m членов, называется остатком ряда (1.1):

(1.2)

Ряд сходится или расходится вместе со своим остатком.

Рассмотрим примеры.

Пример1: Пусть дана бесконечная последовательность . Рассмотрим ряд: . Его «n-ая» частичная сумма равна: . Рассмотрим случаи:

а) найдём , т.е. конечный предел существует и он равен конечному числу (сумма бесконечно убывающей геометрической прогрессии).

б) при этом: и тогда ряд расходится.

в) Пусть . В этом случае ряд имеет вид: 1+1+1+…+1+… . При этом частичная сумма и . Значит ряд расходится (по определению).

г) Пусть . В этом случае ряд имеет вид: 1–1+1–1+1–… . При этом сумма 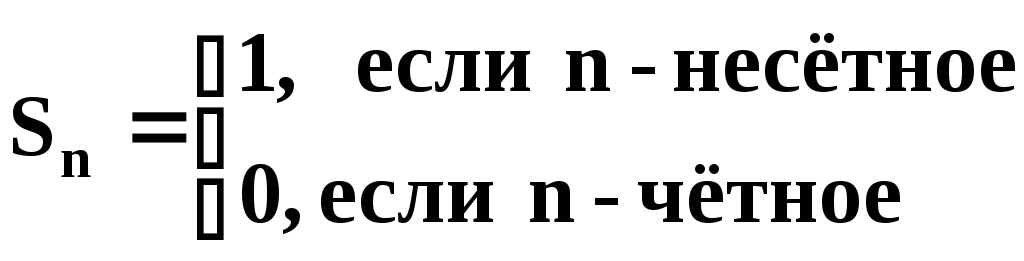, а тогда предел последовательности частичных сумм не существует и ряд не сходится. Т.о. имеем: исходный ряд сходится если и расходится, если .

Пример 2: Рассмотрим ряд: . Заметим, что . При этом n–ая частичная сумма ряда равна:

и тогда . Таким образом, установили, что ряд сходится и сумма его равна 1.

Пример 3: Рассмотрим ряд: . Рассмотрим частичные суммы ряда с номером :

Т.о. имеем, что если , т.к. меньшая сумма стремится к бесконечности. Но мы рассмотрели только подпоследовательность последовательности частичных сумм. Последовательность является возрастающей последовательностью. Тогда и она будет стремиться к бесконечности, т.е. исходный (гармонический) ряд становится расходящимся.

1.2.2. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА

Теорема 1. Если ряд (1.1) сходится, то его общий член стремится к нулю:

(2.1)

Доказательство:

Пусть ряд сходится. Тогда по определению существует - конечное число. Но тогда и , так как, если , то и . Но так как , то .

Следствие. Если , то ряд (1.1) расходится

Замечание: По необходимому признаку сходимости нельзя сделать вывод о сходимости ряда, но если необходимый признак ряда не выполняется (), то можно сделать вывод о его расходимости.

Теорема 2. (Свойства сходящихся рядов)

Свойство 1. Если сходятся ряды:

(1) (2)

И их суммы равны соответственно и , то ряд также сходится и его сумма равна .

Доказательство:

Пусть – «n»–ная частичная сумма рассматриваемого ряда, тогда . Далее, из определения предела следует, что:

Свойство 2. Если сходится ряд: и его сумма равна , тогда ряд , где также сходится и его сумма равна . Доказательство аналогично (провести самостоятельно).

Ряд, получающийся из исходного ряда путём отбрасывания конечного числа его первых членов называется остатком ряда. Остаток ряда есть в свою очередь также ряд.

Теорема 3. Ряд сходится тогда и только тогда, когда сходится его остаток.

Доказательство:

Рассмотрим частичную сумму ряда: () или

, , . Здесь величина – есть постоянное число. Если исходный ряд сходится, то существует конечный предел последовательности частичных сумм: , но и тогда из существования конечного предела в левой части равенства влечёт существование предела в правой части и наоборот.

Т.о. отбрасывание конечного числа членов ряда не влияет на его сходимость.

При изучении рядов, как правило, решаются две задачи: исследование на сходимость или расходимость, нахождение суммы ряда в случае его сходимости. Последний вопрос является существенно проблематичнее и не всегда решаем.

1.2.3. Знакопостоянные ряды.

Рассмотрим ряды с положительными слагаемыми:

(2.1)

(2.2), где

Тогда для них справедливы следующие теоремы:

Теорема 4: Для того, чтобы ряд (2.1) сходился необходимо и достаточно, чтобы последовательность частичных сумм была ограничена.

Доказательство:

Если ряд сходится, то по определению сходящегося ряда существует конечный предел последовательности его частичных сумм: . Но это означает, что . Но это и означает, что последовательность частичных сумм, являясь возрастающей, сверху ограничена своим предельным значением.

Пусть дано, что последовательность частичных сумм ограничена сверху. Но эта последовательность есть возрастающая последовательность (т.к. все ). Тогда по теореме Вейерштрасса она имеет предел: . Т.е. ряд сходится.

5