
Министерство образования и науки Российской Федерации
Саратовский государственный технический университет
Балаковский институт техники, технологии и управления
Высшая математика
Методические указания к выполнению контрольных заданий
для студентов-заочников
специальности «Химическая технология»
полной и сокращенной формы обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2011
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ.
Перед выполнением контрольного задания студент должен изучить соответствующие разделы курса по учебным пособиям в разделе «Литература» настоящих методических указаний. В начале каждой контрольной работы номера необходимых для этой работы пособий указываются в квадратных скобках. В методических указаниях даются также некоторые начальные теоретические сведения и приводятся решения типовых примеров.
Задачи контрольной работы выбираются из таблицы вариантов, помещенной в конце методического пособия, согласно тому варианту, номер которого совпадает с последней цифрой учебного номера (шифра) студента. Контрольную работу следует выполнять в тетради (отдельной для каждой работы) чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. В заголовке работы должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы. Заголовок работы надо поместить на обложке тетради; здесь же следует указать дату отсылки работы в институт и адрес студента. Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными соответствующего номера. Решения задач излагать подробно и записывать аккуратно, объясняя все действия и делая необходимые чертежи. После получения прорецензированной работы (как не зачтенной, так и зачтенной) студент должен исправить в ней все отмеченные ошибки и недочеты.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента.
Контрольная работа № 1.
![]()
Аналитическая геометрия. Элементы векторной и
линейной алгебры.
Л и т е р а т у р а: [1], гл.III, IX, X; [2], §1-6, § 7-13; [4], гл. VII, § 1-5; [5], гл. I, II, III; [6], гл. I, II, III.
1.Совокупность чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей.
Обозначают матрицу буквами А,В,С,…
![]()
![]()
![]()

Матрица размером m x n.
а11,а12,…,аmn-элементы матрицы.
Коротко записывают так: А=(аij), где i-номер строки, j-номер столбца. Матрица размера n x n называется квадратной матрицей n-го порядка.
Элементы a11,a22,…,аnn образуют главную диагональ матрицы, элементы аm1,аm-1,2…,а1,n-побочную диагональ матрицы. Матрица А=(а11,а12,…,а1n) называется матрицей-строкой размером 1 х n.
Матрица
 - матрица-столбец размером m x 1.
- матрица-столбец размером m x 1.
Квадратная матрица
 -
называется единичной матрицей.
-
называется единичной матрицей.
Матрица Ат, которая получается из данной матрицы А заменой строк столбцами, называется транспонированной к А:

Произведением матрицы А=(аij), имеющей m строк и k столбцов, на матрцуВ=(вij), имеющую k строк и n столбцов, называется матрица С=АВ=(сij), имеющая m строк и n столбцов, каждый элемент сij которой равен сумме произведений элементов i-й строки матрицы А и j-го столбца матрицы В:
Сij=аi1в1j+аi2в2j+…+аikаkj
2.Определитель- это число, поставленное по определенным правилам в соответствие квадратной матрице.
Обозначается
D=detА=![]()
Определитель второго порядка:
![]()


Определитель третьего порядка:
 (1)
(1)
Вычисляется по правилу треугольника. Схематически это выглядит так:















Минором Мij какого-либо элемента определителя n-го порядка называется определитель n-1 порядка, получаемый из данного определителя вычеркиванием i строки и j столбца, на пересечении которых стоит элемент.
Например:
![]() ,
,
![]() - миноры элементов a11
и a31
определителя D.
- миноры элементов a11
и a31
определителя D.
Алгебраическим дополнением Аij какого-либо элемента аij называется его минор Мij, умноженный на (-1)i+j,где i,j –номера строки и столбца элемента аij:
Aij=(-1)i+jMij (2)
Матрица А-1 называется обратной по отношению к матрице А, если выполняется равенство:
A-1A=AA-1=E
Если определитель D матрицы А не равен 0, то обратная матрица вычисляется по формуле:
![]() ,
(3)
,
(3)
где
![]() - присоединенная матрица, составляется
из алгебраических дополнений следующим
образом:
- присоединенная матрица, составляется
из алгебраических дополнений следующим
образом:
 (4)
(4)
-
Элементарными называются следующие преобразования матриц:
а) перестановка строк (столбцов),
б) умножение строк (столбцов) на число, отличное от 0,
в) прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на число.
При помощи элементарных преобразований любую прямоугольную матрицу можно привести к ступенчатому виду. Схематично ступенчатая матрица изображена на рисунке:

Не заштрихованная часть матрицы занята нулями. В клетках, покрытых двойной штриховкой , стоят ненулевые элементы. Они называются угловыми элементами. Остальные элементы могут быть произвольными.
Число r угловых элементов ступенчатой матрицы В не зависит от способа приведения матрицы А к ступенчатому виду и называется рангом матрицы А. Обозначается r(А)=r(В)=r
3. Система 3-х линейных уравнений с тремя неизвестными х1,х2,х3 имеет вид:
 (5)
(5)
где аij – коэффициенты системы, bi- свободные члены.
Определитель 3-го порядка D, составленный из коэффициентов при неизвестных, называется определителем системы:
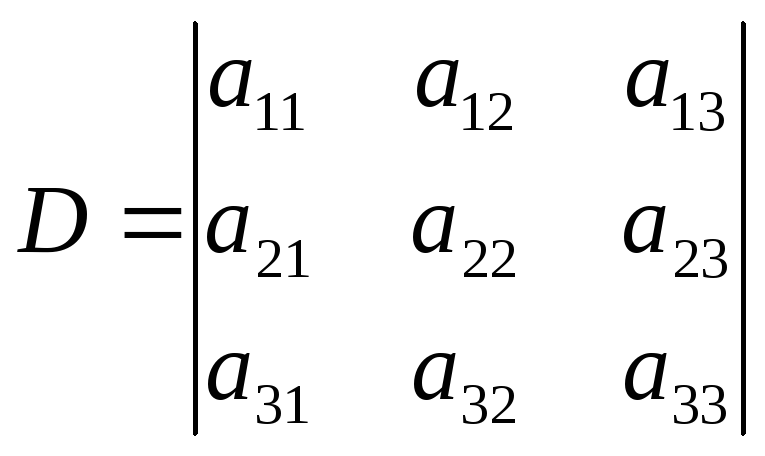
![]()
Решение системы методом Крамера: Если определитель системы D не равен нулю, то решение находится по формулам Крамера:
![]()
![]() ,
(6)
,
(6)
где определители D1, D2, D3 вычисляются следующим образом:
![]()

![]()
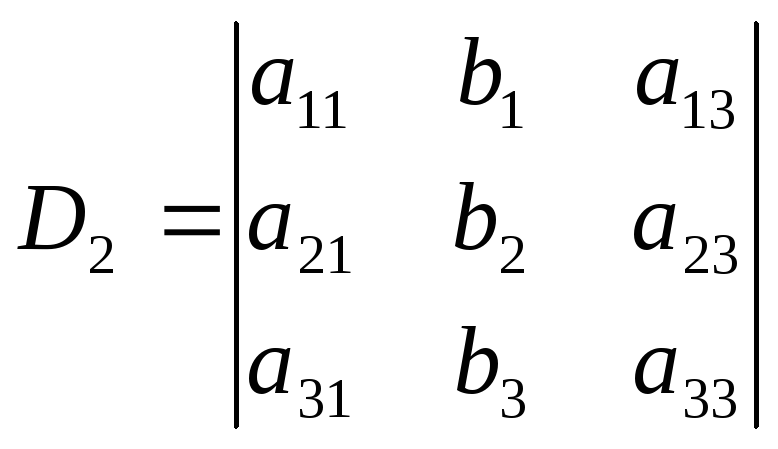
![]()

Систему (5) можно записать в матричной форме:
АХ=В , (7)
где

![]()


Решение системы (1) матричным способом: Если определитель системы D не равен 0, то решение системы имеет вид:
Х=А-1В (8)
4 .Вектором называется отрезок с определенным на нем направлением.
Обозначается
![]() .
.
Координатами
вектора
![]() в прямоугольной системе координат в
пространстве называются его проекции
на оси координат Ох,
Оу,
Оz.
в прямоугольной системе координат в
пространстве называются его проекции
на оси координат Ох,
Оу,
Оz.
Обозначается
![]()
Х= прОх![]() =х2-х1
=х2-х1
У=
прОу![]() =у2-у1
(9)
=у2-у1
(9)
Z= прОz![]() =z2-z1,
=z2-z1,
где точка А(х1,у1,z1)-начало вектора, В(х2,у2,z2)- конец вектора.
Длина вектора вычисляется по формуле:
![]() (10)
(10)
Вектор может быть
разложен по базису
![]() ,
т.е. представлен в виде:
,
т.е. представлен в виде:
![]()
5.Скалярным
произведением двух векторов
![]()
![]() и
и
![]() называется
число, определяемое равенством:
называется
число, определяемое равенством:
![]()
![]() =
=![]() , (11)
, (11)
где
![]() - угол между
векторами
- угол между
векторами
![]() и
и
![]() .
.
Выражение скалярного произведения двух векторов через координаты векторов:
![]()
![]()
![]() =
=![]() ,
(12)
,
(12)
где
![]() ,
,![]()
7. Векторным
произведением двух векторов
![]()
![]() и
и
![]() называется вектор
называется вектор
-
д
 лина
его вычисляется по формуле
лина
его вычисляется по формуле
![]() =
=![]() ,
,
![]() -угол
между векторами
-угол
между векторами
![]()
![]() и
и
![]() ,
,
2) вектор
![]() перпендикулярен векторам
перпендикулярен векторам
![]()
![]() и
и
![]() ,
,
3) векторы
![]()
![]() ,
,![]() ,
,
![]() образуют правую тройку.
образуют правую тройку.
Выражение векторного
произведения через координаты векторов![]()
![]() и
и
![]() :
:
![]() =
=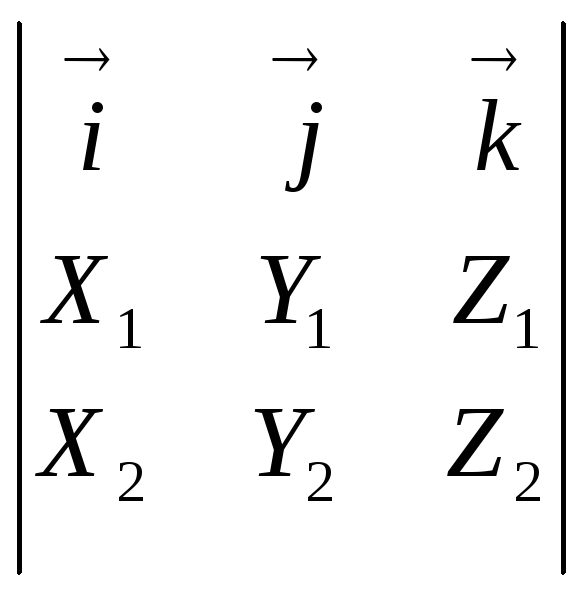 , (13)
, (13)
где Х1,У1,Z1-
координаты вектора
![]() ,
Х2,У2,Z2-
координаты вектора
,
Х2,У2,Z2-
координаты вектора
![]() .
.
Г еометрически
длина векторного произведения равна
площади параллелограмма, построенного
на векторах
еометрически
длина векторного произведения равна
площади параллелограмма, построенного
на векторах
![]() и
и
![]() :
Sпар-ма=
:
Sпар-ма=![]()
8. Смешанным
произведением трех векторов
![]() ,
,![]() ,
,![]() называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора
![]() и векторного произведения
и векторного произведения
![]() х
х![]() :
:
![]()
![]()
![]() =
=![]() (
(![]() х
х![]() )
)
Выражение смешанного произведения векторов через их координаты:
![]() =
= ,
,
где Х1,У1,Z1-
координаты вектора
![]() ,
Х2,У2,Z2-
координаты вектора
,
Х2,У2,Z2-
координаты вектора
![]() ,
Х3,У3,Z3-
координаты вектора
,
Х3,У3,Z3-
координаты вектора
![]() .
.
Модуль смешанного
произведения векторов
![]() ,
,![]() ,
,![]() равен объему параллелепипеда, построенного
на этих векторах:
равен объему параллелепипеда, построенного
на этих векторах:
![]()
![]()
9 .Общее
уравнение плоскости S
имеет вид:
.Общее
уравнение плоскости S
имеет вид:
Ах+Ву+Сz+D=0 (14)
Где
![]() - нормальный вектор плоскости.
- нормальный вектор плоскости.
Уравнение плоскости, проходящей через три точки М0(х0,у0,z0), М1(х1,у1,z1), М2(х2,у2,z2) имеет вид:
 (15)
(15)
Угол между двумя
плоскостями S1
и S2
определяется как угол между их нормальными
векторами![]() и
и
![]() ,
определяется из формулы:
,
определяется из формулы:
 (16)
(16)
10.Уранения прямой в пространстве, проходящей через две точки М0(х0,у0,z0), М1(х1,у1,z1) имеют вид:
![]() (17)
(17)
Пример 1. По координатам вершин пирамиды А1(2,-3,1), А2(-1,-4,2), А3(4,-1,2), А4(3,-4,2) найти: 1.длины ребер А1А2 и А1А3; 2. угол между ребрами А1А2 и А1А3; 3. площадь грани А1А2А3; 4. объем пирамиды А1А2А3А4.
Р е ш е н и е.
1.Находим векторы
![]()
![]()
![]()
Длины этих векторов, т.е. длины ребер А1А2 и А1А3 таковы:
![]()
![]()
-
Скалярное произведение векторов
 находим по формуле (12):
находим по формуле (12):
![]()
Косинус угла между векторами находим по формуле:

3. Площадь грани
А1А2А3
равна половине площади параллелограмма,
построенного на векторах
![]() ,
т.е. половине длины векторного произведения
этих векторов:
,
т.е. половине длины векторного произведения
этих векторов:

![]()
![]()
4) Объем V
пирамиды равен
![]() объема параллелепипеда, построенного
на векторах
объема параллелепипеда, построенного
на векторах![]()
![]() .
.
Координаты вектора
![]()

Пример 2. Найти угол между плоскостью Р1, проходящей через точки А1(2,-3,1),А2(-1,-4,2),А3(4,-1,2) и плоскостью Р2, проходящей через точки А1,А2,А4(3,-4,2).
Р е ш е н и е. Находим уравнения плоскостей Р1 и Р2 по формуле (16):

(x-2)(-3)-(y+3)(-5)+(z-1)(-4)=0
3x-5y+4z-25=0-уравнение
плоскости Р1,
![]() -
нормальный вектор плоскости Р1.
-
нормальный вектор плоскости Р1.

![]() (x-2)0-(y+3)(-4)+(z-1)4=0
y+z+2=0-
уравнение плоскости Р2,
(x-2)0-(y+3)(-4)+(z-1)4=0
y+z+2=0-
уравнение плоскости Р2,
![]() -
нормальный вектор плоскости Р2.
-
нормальный вектор плоскости Р2.
Угол
![]() между плоскостями находим по формуле
(17)
между плоскостями находим по формуле
(17)

![]()
Пример 3. Составить уравнение прямой, проходящей через точки А1(2,-3,1) и А2(-1,-4,2).
Р е ш е н и е. Используя формулу (12), получаем:
![]()
![]() -уравнение искомой
прямой.
-уравнение искомой
прямой.
Пример 4. С помощью формул Крамера найти решение системы:
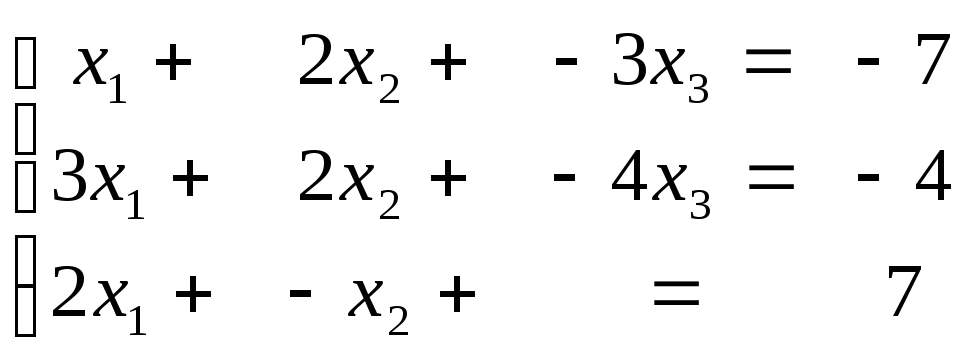
Р е ш е н и е. Находим определитель системы:

Так как D![]() 0,
то решение системы находим по формулам
Крамера:
0,
то решение системы находим по формулам
Крамера:
![]()
![]()
![]()
![]()
Находим D1,D2,D3:
 ;
;
 ;
;
 .
.
Получаем решение
системы:
![]() \=
\=![]()
![]()
Пример 5.
Дана система линейных уравнений 
Найдем решение системы уравнений методом Гаусса. Разделим первое уравнение на 2. Затем умножим обе части этого уравнения на (-3) и прибавим их к соответствующим частям третьего уравнения, и, умножив на (-5), прибавим к соответствующим частям третьего уравнения. В результате получим систему:
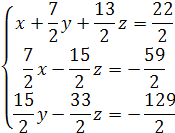
Разделим обе части второго уравнения на 7/2, после этого умножим обе части полученного второго уравнения на (-15/2) и сложим их с соответствующими частями третьего уравнения, в результате получим систему:

Из последнего уравнения находим z=3, затем из второго найдем у=-2, из третьего найдем х=1.
