3.4. Тригонометрический ряд Фурье
Определение. Тригонометрическим
рядом Фурье функции
на отрезке
длины
называется ее ряд Фурье по ортогональной
системе гармоник
,
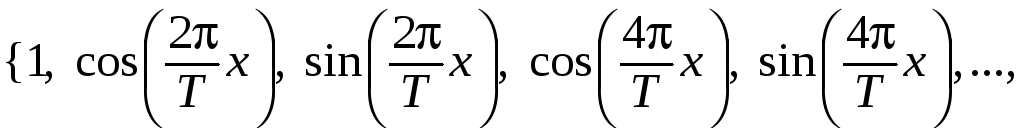
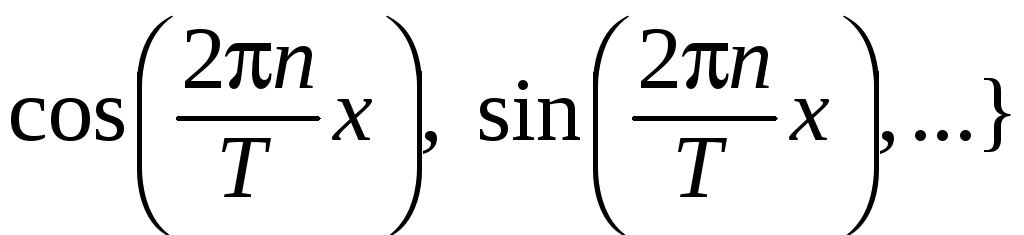то есть функциональный ряд вида
.
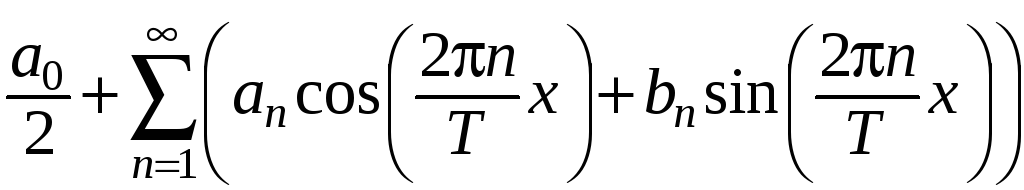(44)
Числа
и
─ коэффициенты ряда Фурье (коэффициент
при единичной функции записан в виде
в целях единообразия дальнейших формул).
Найдем выражения для коэффициентов тригонометрического ряда Фурье. В силу формул (41) и (43):
,
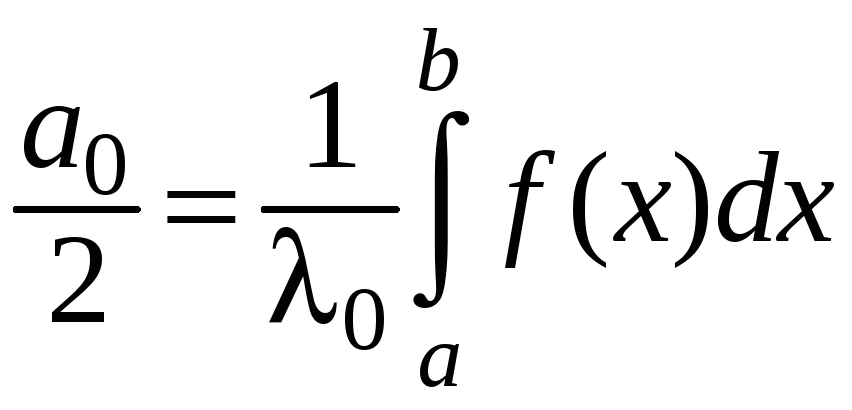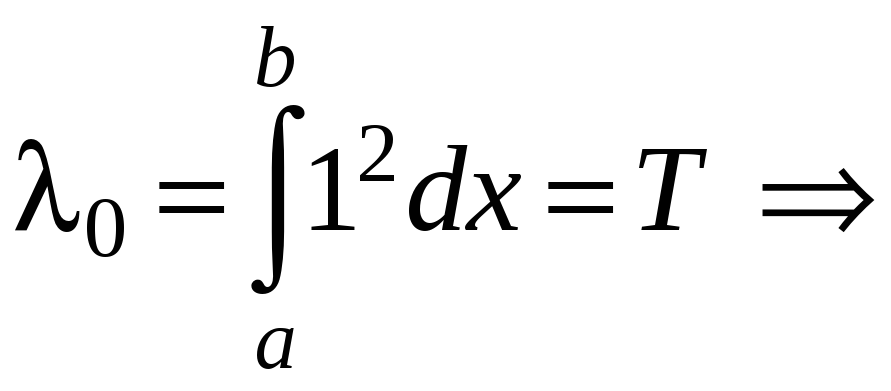
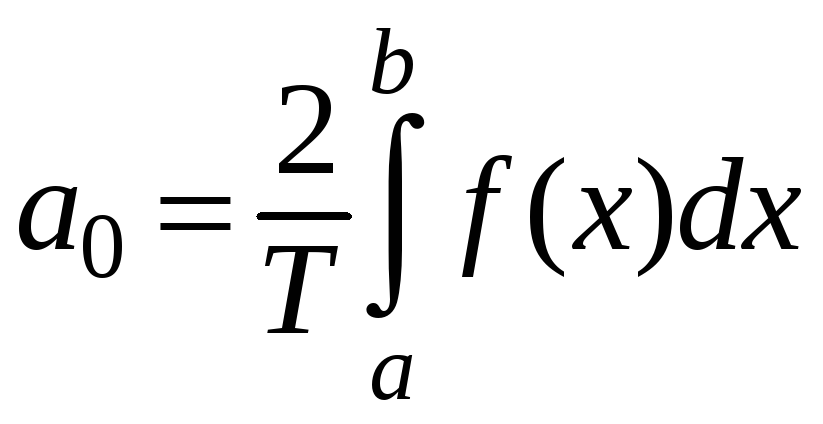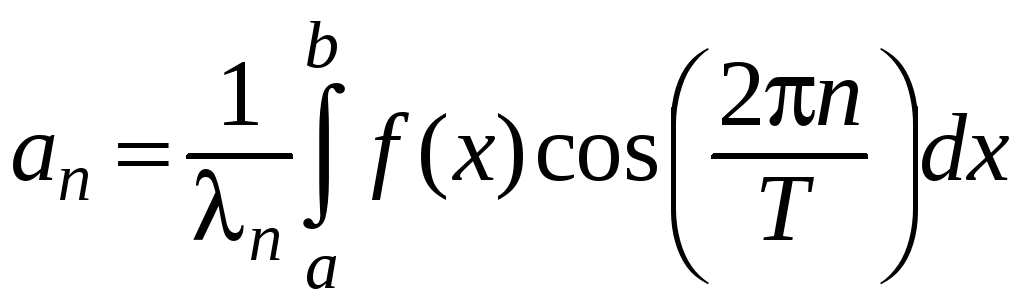где
;
, где
;
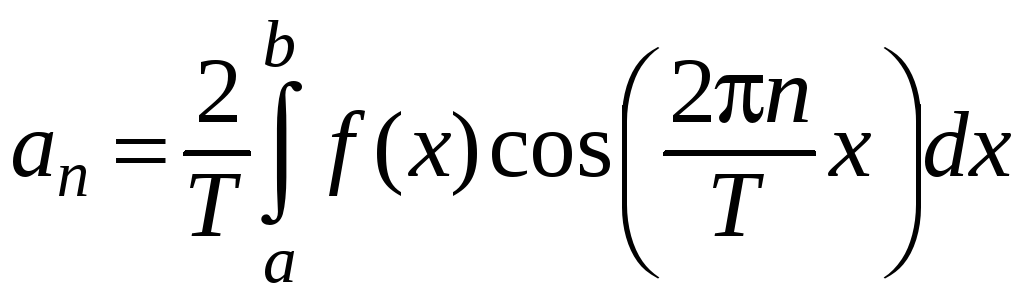аналогично
.
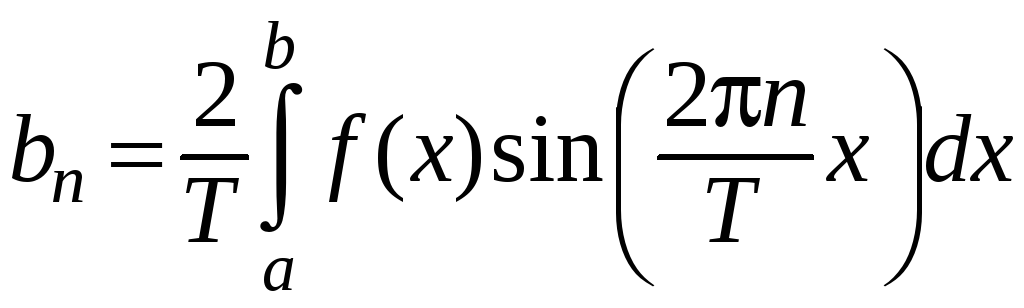Таким образом, коэффициенты тригонометрического ряда Фурье задаются формулами:
;
;
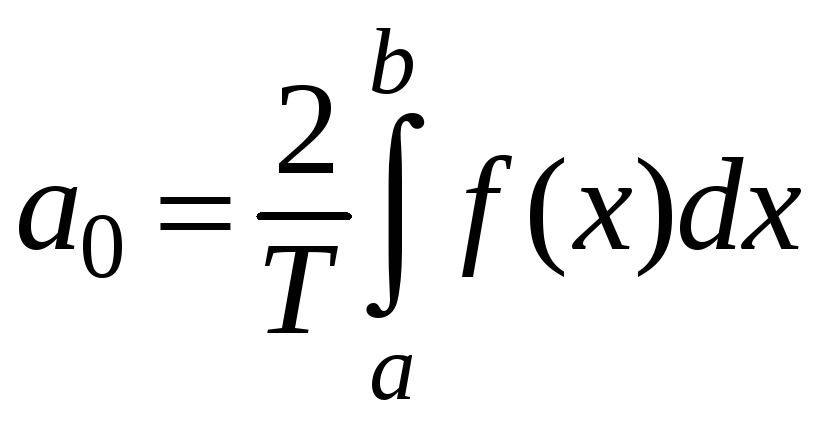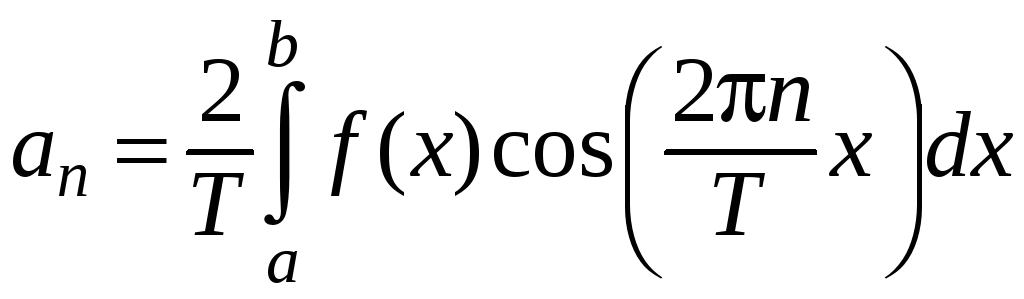(45)
.
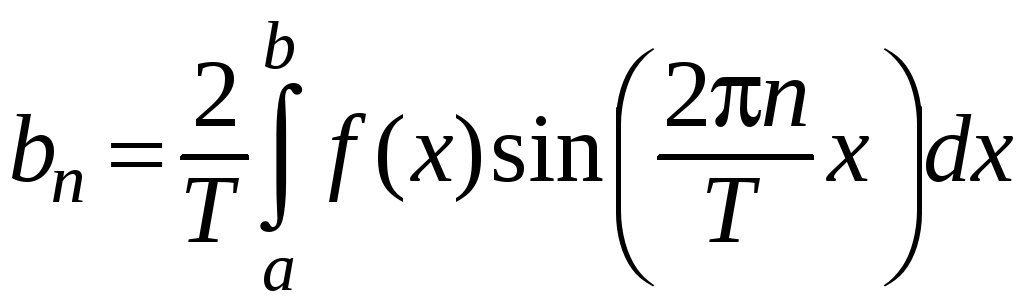Пример. Найдем ряд Фурье функции
на отрезке
.
Здесь
.
Применяя формулу (45) и интегрируя по
частям, получаем следующие значения
коэффициентов ряда:
;
;
.
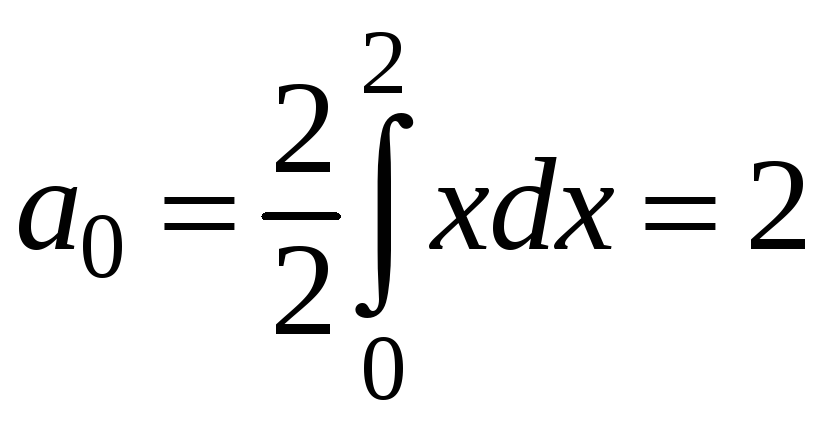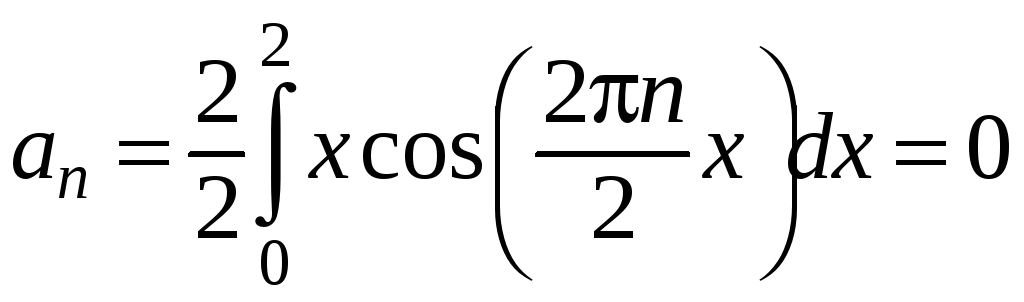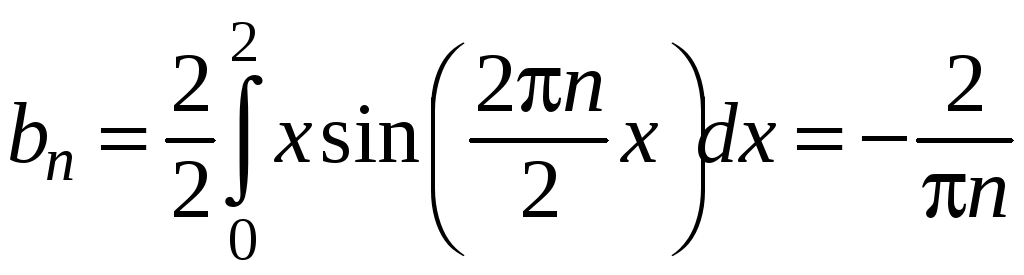Ряд
Фурье имеет вид:
.
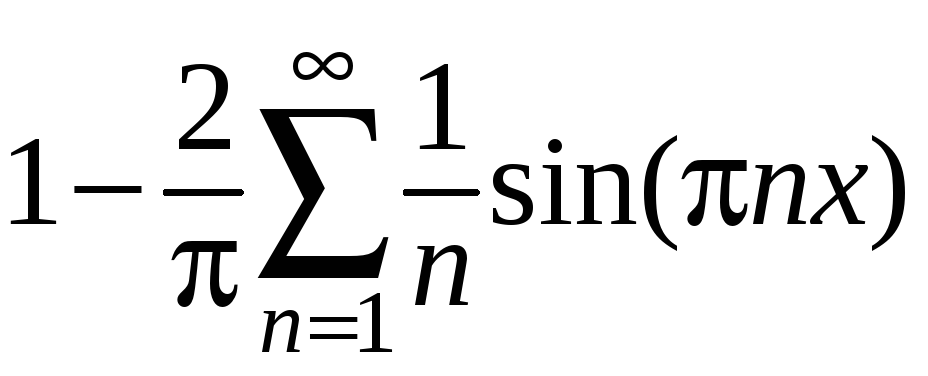3.5. Достаточное условие разложимости функции в ряд Фурье
,
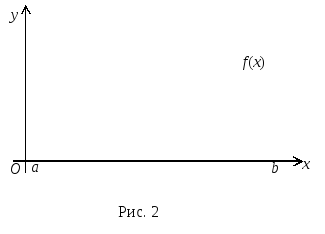
заданная на отрезке
,
называется кусочно-монотонной,
если этот отрезок можно разбить на
конечное число промежутков, на каждом
из которых функция монотонна.
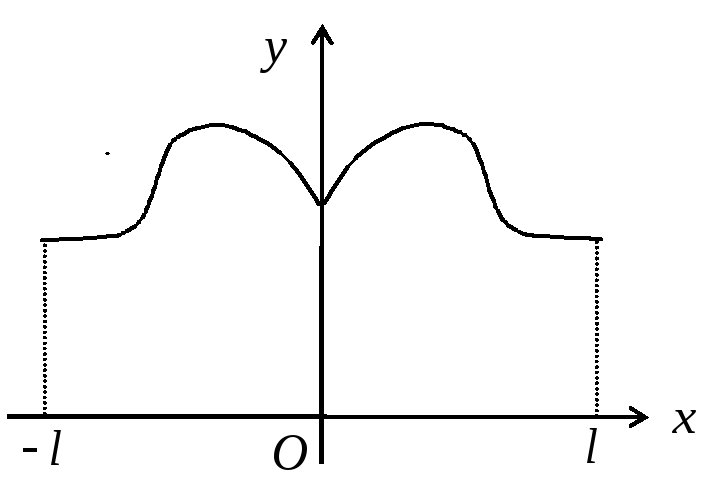
Пример графика кусочно-монотонной функции приведен на рис. 2.
Напомним,
что левосторонний и правосторонний
пределы функции
в точке
обозначаются
и
соответственно.
Для
точки разрыва 1-го рода
среднее арифметическое односторонних
пределов
показано на рис. 3.
Укажем без доказательства, что справедливо следующее достаточное условие разложимости функции в ряд Фурье:
Теорема
(достаточное условие Дирихле). Пусть
функция
удовлетворяет двум условиям:
1)
кусочно-монотонна на отрезке
;
2)
ограничена на отрезке
.
Тогда
ряд Фурье этой функции сходится при
всех
;
при этом для его суммы
справедливо:
,
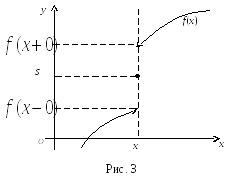если
– внутренняя точка непрерывности
функции;
,
если
– внутренняя точка разрыва 1-го
рода;
,
если
любая из крайних точек отрезка:
или
.
З
амечание.
Сумма ряда Фурье
является периодической функцией с
периодом
,
заданной на всей числовой оси. В тех
точках отрезка
,
в которых
непрерывна, выполняется равенство
.
Вне отрезка
значения
отличаются от
(рис. 4).
3.6. Частные случаи ряда Фурье
I. Ряд Фурье на симметричном отрезке
Если отрезок [a,b] симметричен относительно начала координат, т.е. имеет вид [l,l], то
,
и формулы для коэффициентов ряда Фурье принимают следующий вид:
;
;
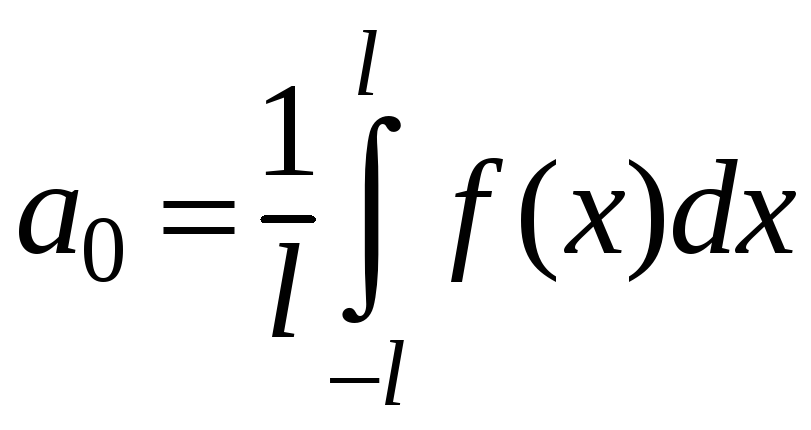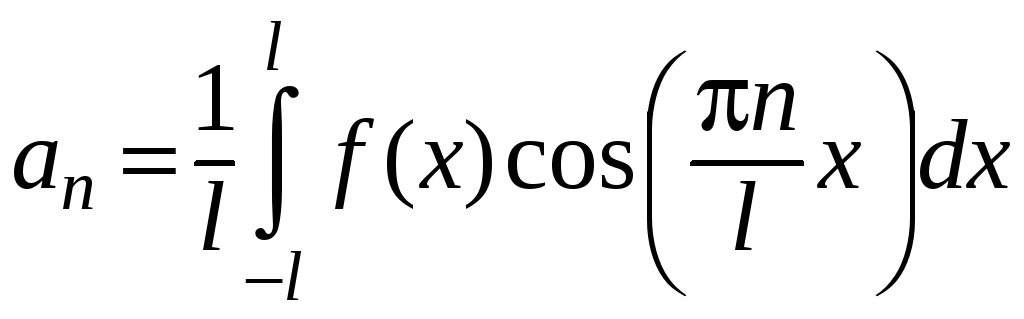(46)
.
-
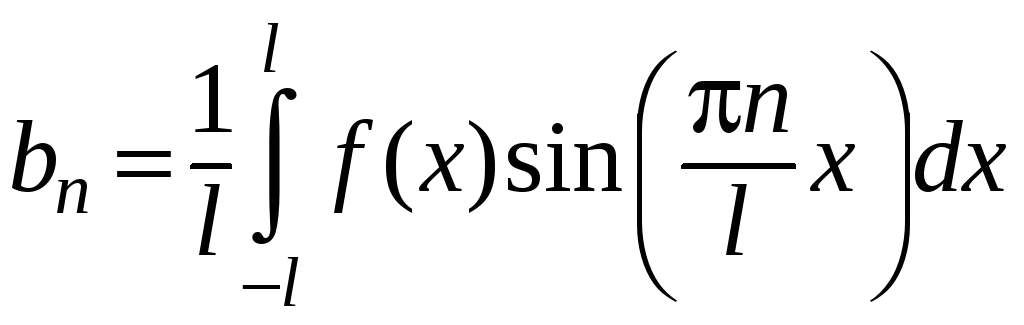II. Ряд Фурье для четной и нечетной функций на симметричном промежутке
Напомним, что для четной функции
,
заданной на симметричном (относительно
точки
)
промежутке
,
имеет место равенство:
.
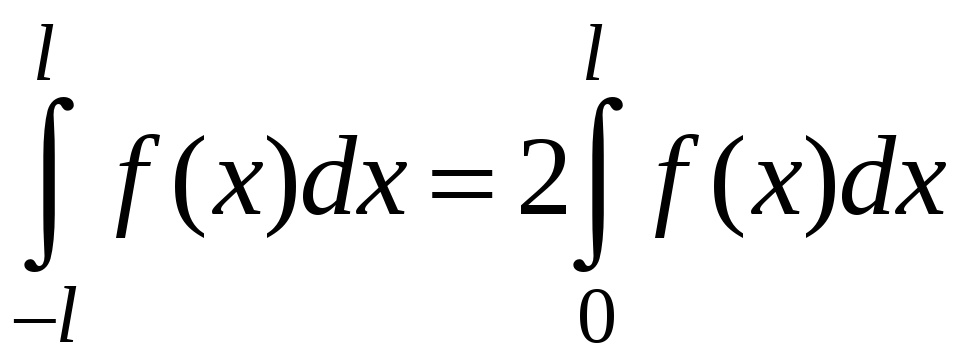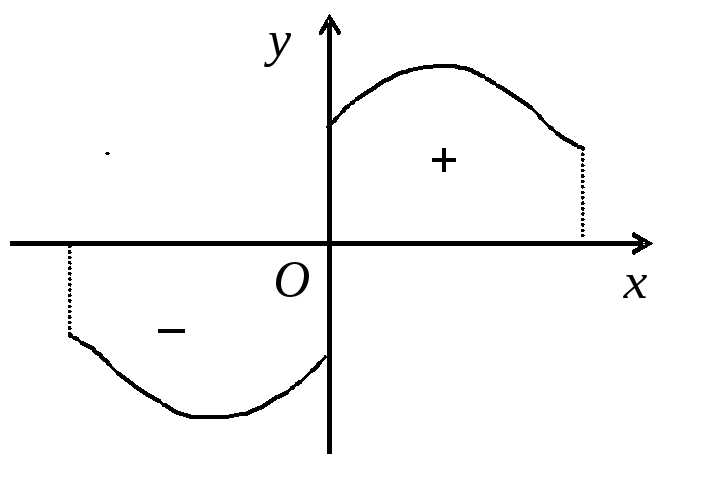
Геометрически это означает, что площадь криволинейной трапеции, симметричной относительно оси ординат, равна удвоенной площади правой половины (Рис. 5).
|
Рис. 5. |
Рис. 6. |
Для
нечетной функции
интеграл по симметричному промежутку
равен нулю, поскольку площади симметричных
частей трапеции, расположенных по разные
стороны оси абсцисс, равны по величине,
но входят в интеграл с противоположными
знаками (Рис. 6). Используем эти свойства
при вычислении коэффициентов Фурье.
Пусть функция
является четной на промежутке
.
Тогда, ввиду четности косинуса, функции
вида
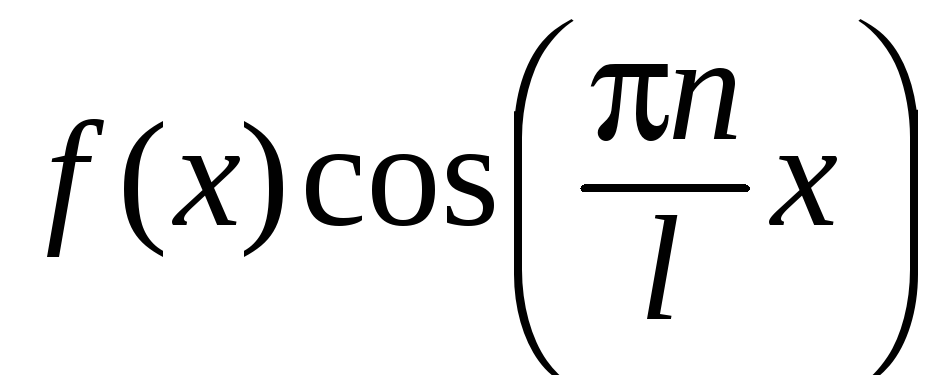также являются четными, и для соответствующих
коэффициентов Фурье:
.
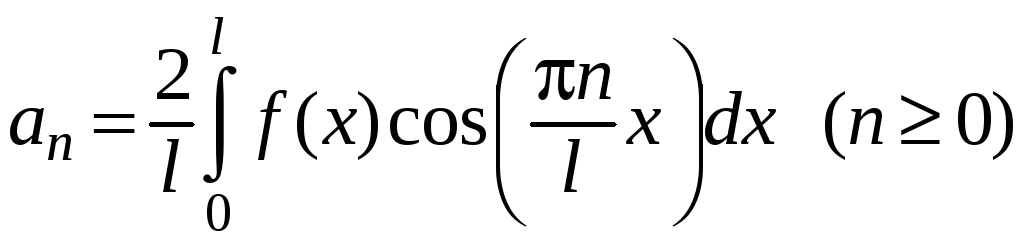(47)
Функции
вида
,
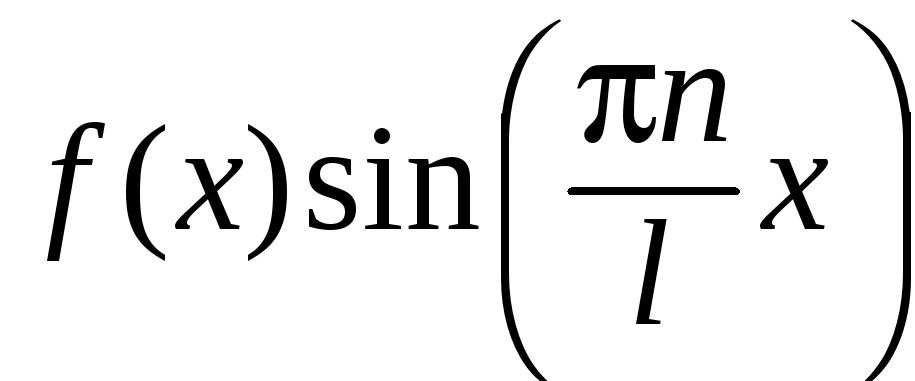ввиду нечетности синуса, являются
нечетными, и для соответствующих
коэффициентов Фурье:
.
(48)
Таким образом,
для
четной функции на промежутке
коэффициенты
при синусах равны нулю, а коэффициенты
при косинусах вычисляются как удвоенные
интегралы по правой половине промежутка;
для нечетной функции
на промежутке
коэффициенты при косинусах равны нулю,
а коэффициенты при синусах вычисляются
как удвоенные интегралы по правой
половине промежутка:
;
(49)
.
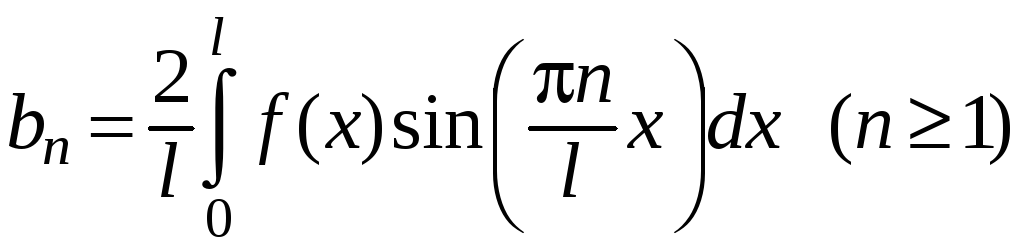(50)
Пример. 
,
— четная функция; здесь
;
аргументы гармоник
.
Поскольку
при x[0,],
имеем (проделайте
соответствующие выкладки!):
;
,
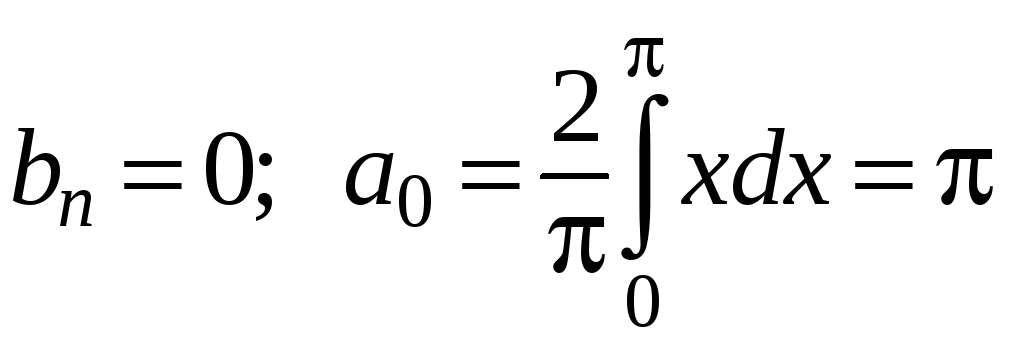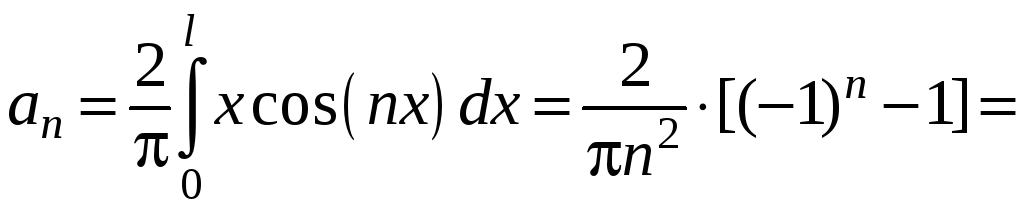
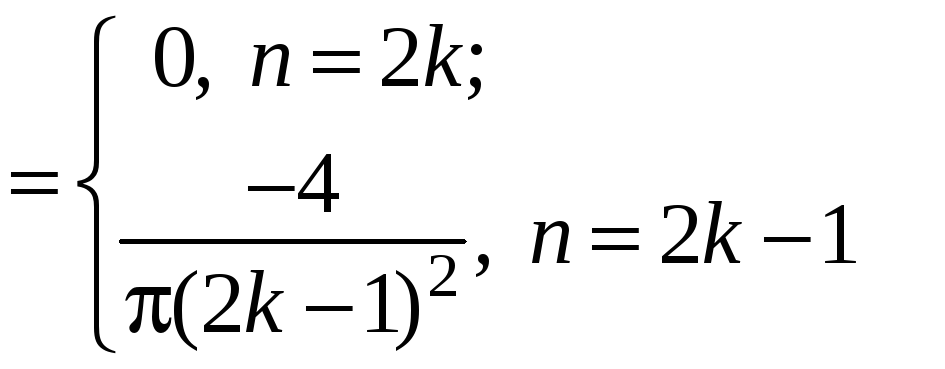где
.
Поскольку
непрерывна и кусочно-монотонна при
,
то на этом отрезке имеет место разложение:
.
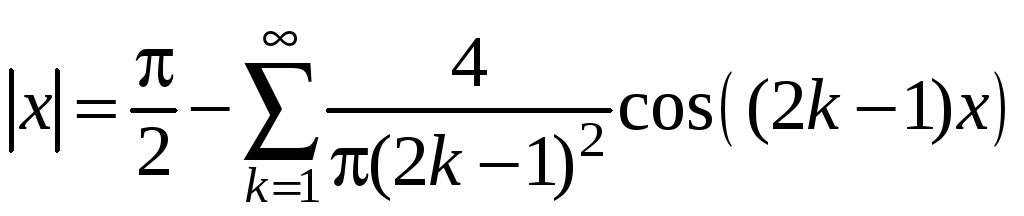