8. Линейное уравнение второго порядка
8.1. Основные понятия
Определение. Линейным уравнением второго порядка называется уравнение вида:
(14)
с
непрерывными на интервале
функциями
и
.
Из
теоремы 2, приведенной на с. 6,
следует, что указанная непрерывность
гарантирует при
существование и единственность решения
задачи Коши с любыми начальными данными
.
Определение. Однородным линейным уравнением второго порядка называется уравнение с нулевой правой частью:
.
(15)
8.2. Свойства решений однородного линейного уравнения
Из
свойств производной следует, что для
любых функций
и любых вещественных чисел
:
.
Обозначим
правую часть уравнений (14) и (15) через
:
.
Тогда
эти уравнения принимают вид
и
соответственно. При этом
,
Теорема 3:
Если
функции
и
являются решениями однородного линейного
уравнения (15),
то функция
также является его решением.
Доказательство.
Пусть
и
.
Тогда
.
▄
8.3. Линейное уравнение с постоянными коэффициентами
Рассмотрим линейное уравнение с постоянными коэффициентами:
(16)
(
и
– постоянные числа), и соответствующее
ему однородное уравнение
.
(17)
Определение. Характеристическим уравнением, соответствующим дифференциальному уравнению (17), называется алгебраическое квадратное уравнение
.
(18)
Отметим,
что второй производной
дифференциального уравнения соответствует
в характеристическом уравнении
.
Коэффициент при первой производной
переходит в коэффициент при первой
степени
.
Наконец, коэффициент при
,
то есть при производной нулевого порядка,
переходит в свободный член (коэффициент
при нулевой степени
).
Примеры.
1. Для
линейного однородного уравнения
соответствующее характеристическое
уравнение записывается в виде
.
2.
Уравнению
соответствует характеристическое
уравнение
.
3.
Уравнению
соответствует характеристическое
уравнение
.
Общее
решение однородного уравнения (17) можно
получить, исходя из корней соответствующего
характеристического уравнения (17). Здесь
возможны три случая в соответствии с
возможным значением его дискриминанта
.
А.
Случай
положительного дискриминанта
Пусть
.
В этом случае уравнение (18) имеет два
различных вещественных корня
и
:
,
что соответствует разложению квадратного трехчлена на множители с вещественными коэффициентами:
.
Можно проверить, что в этом случае общее решение однородного уравнения (16) имеет вид:
.
(19)
Примеры.
1.
;
начальные условия:
.
Соответствующее характеристическое
уравнение:
.
Дискриминант
.
Корни квадратного уравнения
.
Общее решение имеет вид:
.
Найдем частное решение для задачи Коши.
Дифференцируем
общее решение:
.
Подставляем начальные условия в
и
(учитывая, что
):
Решая
эту систему, получаем:
.
Соответствующее решение задачи Коши:
.
2.
.
Характеристическое уравнение
.
Корни квадратного уравнения
.
Общее решение имеет вид:
.
Б.
Случай
нулевого дискриминанта Пусть
.
В этом случае характеристическое
уравнение имеет один вещественный
корень кратности
:
,
что соответствует разложению квадратного трехчлена на множители с вещественными коэффициентами:
.
Можно проверить, что в этом случае общее решение однородного уравнения (17) имеет вид:
.
(20)
Пример.
.
Соответствующее характеристическое
уравнение
.
Дискриминант
.
Кратный корень квадратного уравнения
.
Общее решение имеет вид:
.
В.
Случай
отрицательного дискриминанта Пусть
.
В этом случае уравнение (17) имеет два
различных комплексных корня
и
,
которые задаются формулой:
,
где
.
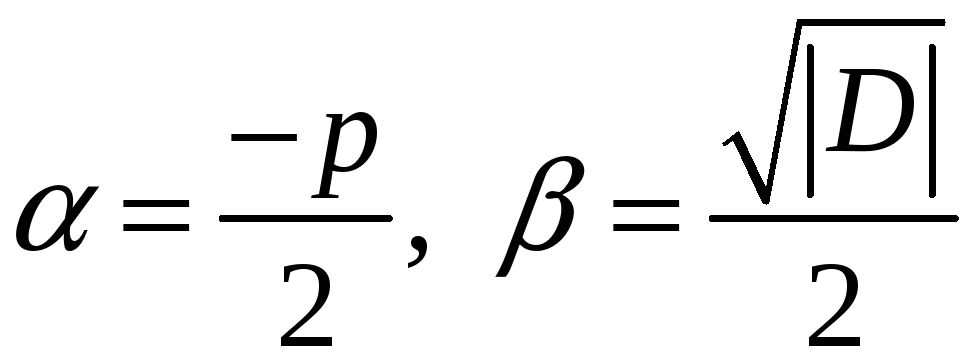К
этим значениям можно придти, используя
формально выражение для корней, полученное
в случае положительного дискриминанта,
и помня, что
обозначает «мнимую единицу» —комплексное
число, для которого
:
.
Можно проверить, что в этом случае общее решение однородного уравнения (17) имеет вид:
.
(21)
Примеры.
1.
.
Соответствующее характеристическое
уравнение
.
Дискриминант
.
Корни квадратного уравнения
.
Общее решение имеет вид:
.
2.
.
Соответствующее характеристическое
уравнение
.
Корни квадратного уравнения
.
Общее решение имеет вид:
.
Найдем
частное решение для задачи Коши с
начальными условиями
.
Дифференцируем общее решение:
.
Подставляем
начальные условия в
и
(учитывая, что
):
Отсюда
.
Соответствующее частное решение
.