5. Однородное уравнение первого порядка

Определение. Однородным уравнением первого порядка называется уравнение, разрешенное относительно производной:

, (9)

в котором функция при всех вещественных удовлетворяет условию:

.

Полагая в этом равенстве , убеждаемся, что правая часть зависит только от отношения переменных : .

Приведем примеры таких функций:

1) ; 2) . Напротив, функция , как легко проверить, не удовлетворяет условию .

Введем новую искомую функцию , так что . Тогда формула для производной произведения дает: ,  и уравнение (9) принимает вид:

—

уравнение с разделяющимися переменными относительно новой искомой функции . Если для него найден общий интеграл (методом, описанным в предыдущем разделе):

,

то, заменяя в нем на , получим общий интеграл для исходной неизвестной функции :

.

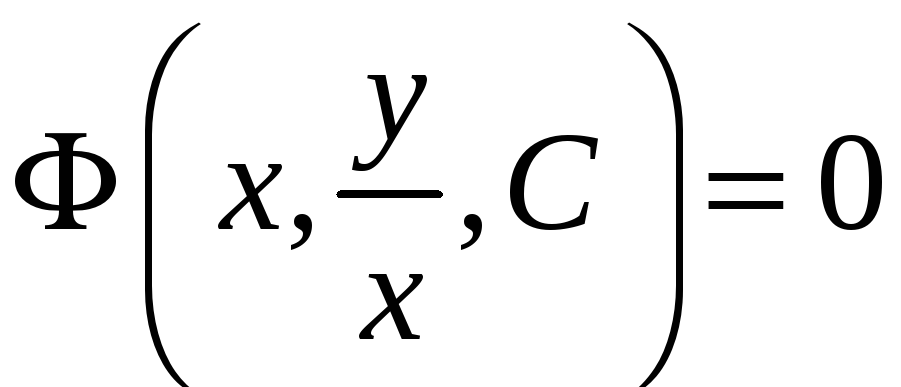Алгоритм решения однородного уравнения первого порядка:

1. Проверка однородности: .

2. Введение новой искомой функции .

3. Замена в уравнении   на , на .

4. Решение полученного уравнения с разделяющимися переменными относительно .

5. Замена в полученном общем интеграле на .

Пример. Решим уравнение . Здесь 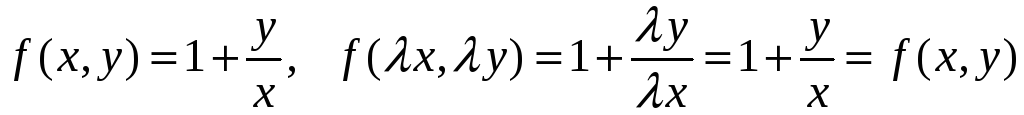, так что уравнение, действительно, является однородным. После введения новой переменной получаем уравнение:

.

Заменяя на , получаем общий интеграл для исходной неизвестной функции : .

6. Линейное уравнение первого порядка

Определение. Линейным уравнением первого порядка называется уравнение вида: с непрерывными функциями и .

Будем искать общее решение методом И.Бернулли в виде произведения двух новых неизвестных функций: , что дает определенную свободу в выборе одного из множителей, позволяя придать ему необходимый для дальнейшего вид. Тогда . Подставляя эти выражения в исходное уравнение, получим:

.

Группируя слагаемые с , получаем: .

Потребуем от функции , чтобы множитель в квадратных скобках при тождественно обращался в нуль:

(10)

Уравнение (10) является уравнением с разделяющимися переменными. Найдем его частное решение (без произвольной постоянной):

(10) .

Интегрируем обе части:

; ; ;

выбираем в качестве частного решения функцию (здесь символом неопределенного интеграла обозначена какая-либо первообразная функции ) .

Теперь подстановка найденной функции в (10) дает уравнение с разделяющимися переменными относительно :

.

В итоге получаем общее решение:

;

. (11)

Хотя при решении линейного уравнения можно сразу выписывать общий интеграл по формуле (11), представляется полезным проследить на примере всю цепочку выкладок, приводящих к (11).

Пример. Рассмотрим линейное уравнение:

на интервале с начальными условиями .

Здесь . Полагаем:

.

Подставляем в уравнение выражения для и :

.

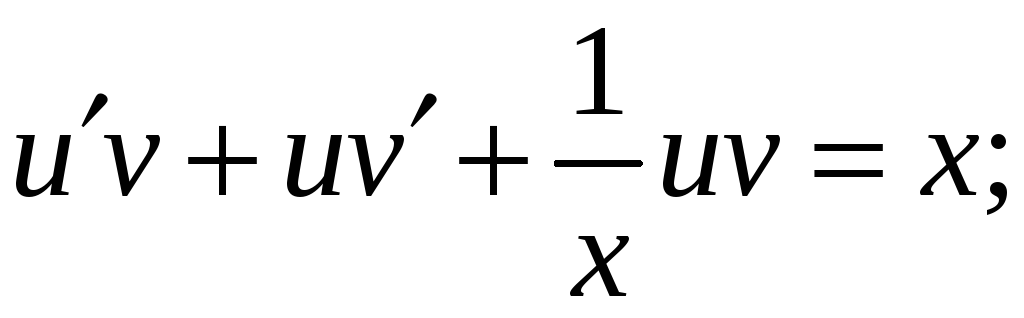. (12)

Накладываем на условие: тогда

, и можно выбрать . Подставляем в (12) и учитываем, что, в соответствии с выбором функции , выражение в квадратных скобках тождественно равно нулю:

.

Функция

является общим решением.

Найдем частное решение задачи Коши. Подставим для этого начальные условия в общее решение и найдем соответствующее значение константы :

Подставив найденное значение в общее решение, получаем решение задачи Коши:

.