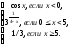- •Практические занятия
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •4). (Задание для самостоятельного решения).
- •3). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •Исполнительский блок
- •Контролирующий блок
Исполнительский блок
Индивидуальные домашние задания (контрольная работа)
Правила выполнения и оформления контрольной работы
При выполнении контрольной работы надо строго придерживаться указанных ниже правил:
-
Студент должен выполнять контрольные задания по варианту, определенному преподавателем при выдаче ИДЗ (возможны другие способы определения). Контрольные работы, выполненные не по своему варианту, не зачитываются;
-
Контрольную работу следует выполнять в тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний преподавателя;
-
В заголовке работы должны быть четко написаны фамилия студента, его инициалы, номер контрольной работы (номер модуля или его название). Заголовок работы надо поместить на обложке тетради;
-
Решение задач располагать в порядке номеров, указанных в заданиях, сохраняя номер задачи.
-
Перед решением каждой задачи надо выписать полностью ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера;
-
Решения задач следует излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.

Задание 1. Дана функция у=f(x). Указать:
а) область определения D; б) множество значений Е;
в) особенности (четность, нечетность, симметричность графика, периодичность)

Задание 2. Построить схематически графики функций. Для функции у=f(x) найти значения в указанных точках a, b, c. Исследовать на непрерывность.
2.1
а)
 ; б)
; б) а=-5; b=4;
c=5; в)
y=xsign(cosx).
а=-5; b=4;
c=5; в)
y=xsign(cosx).
2.2
a)
 ; б)
; б) a=2;
b=3,5;
c=5; в)
a=2;
b=3,5;
c=5; в)
 .
.
2.3
a)
 ; б)
; б)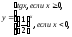 а= -
а= - ;
b=0;
c=
;
b=0;
c= ; в)
y=(3x+1).
; в)
y=(3x+1).
2.4
a)
 ; б)
; б) а= -
а= - ;
b=
;
b= ;
c=16; в)
;
c=16; в)
 .
.
2.5
a)
 ; б)
; б) а=2; b=0,5;
c=5; в)
а=2; b=0,5;
c=5; в)
 .
.
2.6
a)
 ; б)
; б) а= -1; b=0;
c=4;
в)
а= -1; b=0;
c=4;
в)
 .
.
2.7
а)
 ; б)
; б) а=-3; b=0;
c=4; в)
а=-3; b=0;
c=4; в)
 .
.
2.8
а)
 ;
б)
;
б) а=-4; b=1;
c=4;
в)
а=-4; b=1;
c=4;
в)

2.9
a)
 ; б)
; б) а=-1; b=0;
c=4; в)
а=-1; b=0;
c=4; в)
 .
.
2.10
a)
 ;
б)
;
б) а=-1; b=0,5;
c=5;
в)
а=-1; b=0,5;
c=5;
в) .
.
2.11
a)
 б)
б) а=
а=
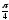 ;
b=-
;
b=- ;
c=
;
c= ;
в)
;
в)
 .
.
2.12
a)
 ;
б)
;
б) а=-1; b=2;
c=4;
в)
а=-1; b=2;
c=4;
в)
 .
.
2.13
a)
 ; б)
; б) а=0; b=1;
c=2;
в)
а=0; b=1;
c=2;
в)
 .
.
2.14
a)
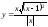 ;
б)
;
б) а=-2; b=0,5;
c=4;
в)
а=-2; b=0,5;
c=4;
в) .
.
2.15
а)
 ; б)
; б) а=-1; b=0,5;
c=2; в)
а=-1; b=0,5;
c=2; в)
 .
.
2.16
a)
 ;
б)
;
б) а= -
а= - ;
b=1;
c=3;
в) y=cosxsignx.
;
b=1;
c=3;
в) y=cosxsignx.
2.17
a)
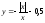 ; б)
; б) а=0; b=3;
c=5;
в) y=
а=0; b=3;
c=5;
в) y= .
.
2.18
a)
 ;
б)
;
б) а=-0,5; b=0;
c=1;
в)
а=-0,5; b=0;
c=1;
в)
 .
.
2.19
a)
 ; б)
; б) а=-1; b=2;
c=9; в)
а=-1; b=2;
c=9; в)
 .
.
2.20
a)
 ; б)
; б) а= -
а= - ;
b=
;
b= ;
c=
;
c= ; в)
; в)
 .
.
2.21
a)
 ; б)
; б) а=
а=
 ;
b=
;
b= ;
c=
;
c=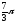 ; в)
; в)
 .
.
2.22
a)
 ; б)
; б) а=-1; b=
а=-1; b= ;
c=
;
c= ; в)
; в)
 .
.
2.23
a)
 ; б)
; б) а=-1; b=2;
c=4;
в)
а=-1; b=2;
c=4;
в)
 .
.
2.24
a)
 ;
б)
;
б) а= -
а= - ;
b=
;
b= ;
c=3;
в)
;
c=3;
в)
 .
.
2.25
a)
 ; б)
; б) а=-1; b=1;
c=3;
в)
а=-1; b=1;
c=3;
в)
 .
.
2.26
a)
 ;
б)
;
б) а=0; b=3;
c=5; в)
а=0; b=3;
c=5; в)
 .
.
2.27
a)
 ; б)
; б) а=-2; b=1;
c=4; в)
а=-2; b=1;
c=4; в)
 .
.
2.28
a)
 ;
б)
;
б) а=0; b=2;
c=3;
в)
а=0; b=2;
c=3;
в) .
.
2.29
a)
 ; б)
; б) а=0; b=4;
c=5; в)
а=0; b=4;
c=5; в)
 .
.
2.30
a)
 ;
б)
;
б)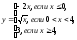 а=-1; b=3;
c=5; в)
а=-1; b=3;
c=5; в) .
.
Задание 3. Выделив полный квадрат и осуществив перенос начала координат, построить в декартовой прямоугольной системе координат параболу. Укажите координаты вершины и точки пересечения параболы с осями координат:
3.1
 ; 3.2
; 3.2
 ; 3.3
; 3.3
 ;
;
3.4
 ; 3.5
; 3.5
 ; 3.6
; 3.6
 ;
;
3.7
 ; 3.8
; 3.8
 ; 3.9
; 3.9
 ;
;
3.10
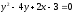 ; 3.11
; 3.11
 ; 3.12
; 3.12
 ;
;
3.13
 ; 3.14
; 3.14
 ; 3.15
; 3.15
 ;
;
3.16 ; 3.17
; 3.17
 ; 3.18
; 3.18
 ;
;
3.19
 ; 3.20
; 3.20
 ; 3.21
; 3.21
 ;
;
3.22
 ; 3.23
; 3.23
 ; 3.24
; 3.24
 ;
;
3.25
 ; 3.26
; 3.26
 ; 3.27
; 3.27
 ;
;
3.28
 ; 3.29
; 3.29
 ; 3.30
; 3.30
 .
.
Задание
4. 1). В полярной системе координат
построить кривую, давая значения
 через
через
 от 0 до
от 0 до
 .
Найти уравнение кривой в декартовой
прямоугольной системе координат. 2).
Найти полярное уравнение кривой и
построить ее:
.
Найти уравнение кривой в декартовой
прямоугольной системе координат. 2).
Найти полярное уравнение кривой и
построить ее:
|
4.1
а)
|
4.2
а)
|
4.3
а)
|
|
4.4
а)
б)
|
4.5
а)
б)
|
4.6
а)
б)
|
|
4.7
а)
б)
|
4.8
а)
б)
|
4.9
а)
б)
|
|
4.10
а)
б)
|
4.11
a)
|
4.12
a)
б)
|
|
4.13
a)
б)
|
4.14
a)
б)
|
4.15
a)
б)
|
|
4.16
a)
б)
|
4.17
a)
б)
|
4.18
a)
б)
|
|
4.19
a)
б)
|
4.20
a)
б)
|
4.21
a)
б)
|
|
4.22
a)
|
4.23
a)
|
4.24
a)
|
|
4.25
a)
б)
|
4.26
a)
б)
|
4.27
a)
б)
|
|
4.28
a)
б)
|
4.29
a)
б)
|
4.30
a)
б)
|
Задание 5. Построить кривую, заданную параметрически:
5.1
 ; 5.2
; 5.2
 ;
5.3
;
5.3
 ; 5.4
; 5.4
 ;
5.5
;
5.5
 ; 5.6
; 5.6
 ; 5.7
; 5.7
 ;
5.8
;
5.8
 ;
5.9
;
5.9
 ;
5.10
;
5.10
 ;
5.11
;
5.11
 ;
5.12
;
5.12
 ;
5.13
;
5.13
 ;
5.14
;
5.14
 ;
5.15
;
5.15 ;
5.16
;
5.16
 ;
5.17
;
5.17
 ;
5.18
;
5.18
 ;
5.19
;
5.19
 ;
5.20
;
5.20
 ;
;
5.21
 ;
5.22
;
5.22
 ;
5.23
;
5.23
 ;
5.24
;
5.24
 ;
;
5.25
 ;
5.26
;
5.26
 ;
5.27
;
5.27
 ;
5.28
;
5.28
 ;
5.29
;
5.29
 ; 5.30
; 5.30
 .
.
Задание
6. В выражении
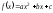 найти значения
найти значения
 и
и
 ,
для которых справедливо заданное
тождество:
,
для которых справедливо заданное
тождество:
6.1
 6.2
6.2
 6.3
6.3

6.4
 6.5
6.5
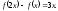 6.6
6.6

6.7
 6.8
6.8
 6.9
6.9

6.10
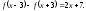 6.11
6.11
 6.12
6.12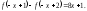
6.13
 6.14
6.14
 6.15
6.15

Найти
значения
 и
и
 для которых справедливо тождество:
для которых справедливо тождество:
6.16
 6.17
6.17

6.18
 6.19
6.19

6.20
 6.21
6.21

6.22
 6.23
6.23

6.24
 6.25
6.25
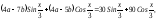
6.26
 6.27
6.27

6.28
 6.29
6.29

6.30.
Задание
7. Описать перечислением всех элементов
множества

 если:
если:
7.1 а)

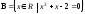 ,
,
б)
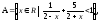
 .
.
-
а)



б)

 .
.
7.3
а)


б)

 .
.
7.4
а)


б)

 .
.
7.5 а)


б)

 .
.
7.6
а)


б)

 .
.
7.7 а)


б)

 .
.
7.8
а)

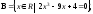
б)

 .
.
7.9
а)
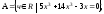

б)

 .
.
7.10
а)


б)

 .
.
7.11 а)


б)

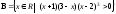 .
.
7.12 а)
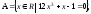

б)

 .
.
7.13 а)


б)

 .
.
-
а)


б)

 .
.
7.15 а)


б)

 .
.
7.16 а)


б)

 .
.
7.17 а)

 .
.
б)

 .
.
7.18 а)


б)


 .
.
7.19 а)


б)

 .
.
7.20 а)


б)

 .
.
7.21 а)


б)

 .
.
7.22 а)


б)

 .
.
7.23 а)


б)
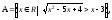
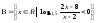 .
.
7.24 а)


б)


7.25 а)


б)

 .
.
7.26 а)


б)

 .
.
7.27
а)


б)

 .
.
7.28 а)


б)

 .
.
7.29 а)


б)

 .
.
7.30 а)


б)



Задание 8. Вычислить пределы.
-
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
-
 ;
;
 ;
;
 ;
;
 ;
;
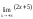
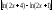 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
-
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
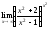 ;
;
 .
.
-
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.5.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.6.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.7.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
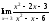 .
.
8.8.
 ;
;
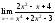 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.9.
 ;
;
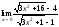 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.10. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.11. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.12. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.13. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.14. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.15.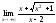 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.16. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
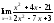 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.17. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.18. ;
;
 ;
;
 ;
;
 ;
.
;
. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.19. ;
;
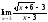 ;
;
 ;
;
 ;
;
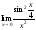 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
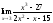 .
.
8.20. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.21. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.22. ;
;
 ;
;
 ;
;
 ;
.
;
. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.23.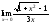 ;
;
 ;
;
 ;
;
 ;
;
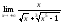 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.24. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.25. ;
;
 ;
;
 ;
; ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.26. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.27. ;
;
 ;
;
 ;
;
 ;
;
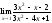 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.28. ;
;
 ;
;
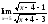 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.29. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8.30. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Задание 9. Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.
|
№ |
Задание |
№ |
Задание |
№ |
Задание |
|
1 |
f(x)= |
11 |
f(x)= |
21 |
f(x)= |
|
2 |
f(x)= |
12 |
f(x)= |
22 |
f(x)= |
|
3 |
f(x)= |
13 |
f(x)= |
23 |
f(x)= |
|
4 |
f(x)= |
14 |
f(x)= |
24 |
f(x)= |
|
5 |
f(x)= |
15 |
f(x)= |
25 |
f(x)= |
|
6 |
f(x)= |
16 |
f(x)= |
26 |
f(x)= |
|
7 |
f(x)= |
17 |
f(x)= |
27 |
f(x)= |
|
8 |
f(x)= |
18 |
f(x)= |
28 |
f(x)= |
|
9 |
f(x)= |
19 |
f(x)= |
29 |
f(x)= |
|
10 |
f(x)= |
20 |
f(x)= |
30 |
f(x)= |

 ;
б)
;
б) .
. ;
б)
;
б) .
. ;
б)
;
б)
 .
. ;
; .
. ;
; .
. ;
; ,
,
 .
. ;
;
 .
. ;
;
 .
. ;
; .
. ;
;
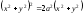 .
. ;
б)
;
б)
 .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
.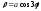 ;
;
 .
.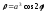 ;
; .
. ;
; .
. ;
б)
;
б)
 .
. ;
б)
;
б)
 .
. ;
б)
;
б)
 .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
.