
- •Практические занятия
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •4). (Задание для самостоятельного решения).
- •3). (Задание для самостоятельного решения).
- •2). (Задание для самостоятельного решения).
- •Исполнительский блок
- •Контролирующий блок
2). (Задание для самостоятельного решения).
Семинар № 6.1 (16). Вычисление пределов функций.
-
Вычислить пределы: 1).
 ;
2).
;
2).
 ;
3).
;
3).
 ;
4).
;
4).
 .
.
Решение.1).
 =
= =-11.
=-11.
2).
 =∞,
так как (х-4)→0 при х→4, (2х+5)→13, тогда
дробь
=∞,
так как (х-4)→0 при х→4, (2х+5)→13, тогда
дробь
 неограниченно возрастает.
неограниченно возрастает.
3).
 ≤
≤ =0.
4).
=0.
4).
 ≤
≤ =∞.
=∞.
Ответ. 1). –11; 2). ∞; 3). 0; 4). ∞.
-
Вычислить пределы:
1).
 ;
2).
;
2).
 ;
3).
;
3).
 ;
4).
;
4).
 .
.
Решение.
1).
 =
= =
= =
= =0.
=0.
2).
 =
= =
= =2.
3).
=2.
3).
 =
= =∞.
=∞.
4). (Задание для самостоятельного решения).
Ответ. 1). 0; 2).2; 3). ∞; 4). 0, если n<m; an/bm , если n=m; ∞, если n>m.
-
Вычислить пределы: 1).
 ;
2).
;
2).
 ;
3).
;
3).

Решение.
1).
 =
= =
= =
-1/2.
=
-1/2.
2).
 =
= =
=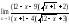 =
= =
-
=
- =
-2/3.
=
-2/3.
3). (Задание для самостоятельного решения).
Ответ. 1).-1/2; 2). –2/3; 3). 6.
-
Вычислить пределы. 1).
 ;
2).
;
2).
 .
.
Решение.
1).
 =
= =
= =
= =0.
=0.
2). (Задание для самостоятельного решения).
Ответ. 1). 0; 2). –1/2.
Задания
для самостоятельного решения: 5)
 ;
6)
;
6)
 ;
7)
;
7)
 ;
8)
;
8)
 ;
;
9)
 ;
10)
;
10)
 ;
11)
;
11)
 .
.
Ответ. 5). –3/2; 6). ∞; 7). ½; 8). 1/3; 9). –2; 10). 2; 11). 1.
Семинар № 6.2 (17). Вычисление пределов функций (замечательные пределы).
-
Вычислить пределы: 1).
 ;
2).
;
2).
 ;
3).
;
3).
 ;
4).
;
4).
 .
.
Решение.
1).
 =
= =5
=5 =5∙1=5.
=5∙1=5.
2).
 =
= =
= =
=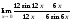 =
= 2.
2.
Задания 3) и 4) для самостоятельного решения. Ответ. 1). 5; 2). 2; 3). 0; 4). 8.
-
Вычислить пределы: 1).
 ;
2).
;
2).
 ;
3).
;
3).
 ;
4).
;
4).
 .
.
Решение.
1).
 .
Проводим замену х-1=у.
.
Проводим замену х-1=у.
Тогда
 =
= =
= =
= =
= =
= =2/π.
=2/π.
Задания 2), 3) и 4) для самостоятельного решения. Ответ. 1). 2/π; 2). –2; 3). 1; 4). 2.
-
Вычислить пределы: 1).
 ;
2).
;
2).
 ;
3).
;
3).

Решение.
1).
 =
= =
= =е2.
=е2.
Задания 2) и 3) для самостоятельного решения. Ответ. 1). е2; 2). 1; 3). ∞.
-
Вычислить пределы: 1).
 ;
2).
;
2).
 .
.
Решение.
1).
 =
= =
= =
= =1.
=1.
2). (Задание для самостоятельного решения). Ответ. 1). 1; 2). 3.
-
Вычислить пределы: 1).
 ;
2).
;
2).
 .
.
Решение.
1).
 .
Проведем замену у=1/х. Тогда
.
Проведем замену у=1/х. Тогда
 =
= =
= =1/
=1/ .
.
2).
(Задание для самостоятельного решения).
Ответ. 1). 1/ ;
2). е.
;
2). е.
-
Вычислить пределы: 1).
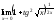 ;
2).
;
2).

Решение.
1).
 =
= =
= =
= =
= =
= .
.
2).
(Задание для самостоятельного решения).
Ответ. 1).
 ;
2). е2.
;
2). е2.
-
Применяя эквивалентные бесконечно малые величины, вычислить пределы:
1).
 ;
2).
;
2).
 ;
3).
;
3).

Решение.
1).
 ~3
~3 ;
sin
;
sin ~
~ ;
1+cos4
;
1+cos4 ~8x.
Тогда
~8x.
Тогда
 =
= =3/8.
=3/8.
Задания
2) и 3) для самостоятельного решения.
Ответ. 1). 3/8;
2).
 ;
3). 3.
;
3). 3.
Семинар № 6.3 (18). Непрерывность функций.
-
Исследовать на непрерывность функции: 1).
 ;
2).
;
2).
 ;
3).
;
3).
 ;
4).
;
4).
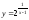 .
.
Решение.
1). Область определения функции х R
кроме х=0, то есть (-∞; 0)
R
кроме х=0, то есть (-∞; 0) (0,
+∞). Так как функция
(0,
+∞). Так как функция
 является элементарной, то, значит, она
непрерывна в области существования.
Точка х=0 является точкой разрыва.
Односторонние пределы
является элементарной, то, значит, она
непрерывна в области существования.
Точка х=0 является точкой разрыва.
Односторонние пределы
 =1
и
=1
и
 =1,
но у(0) не существует.
=1,
но у(0) не существует.

2).
 .
Область определения этой функции х
.
Область определения этой функции х (-∞; 0)
(-∞; 0) (0,
+∞). Она элементарная, а значит непрерывная
в области существования. Односторонние
пределы неравны, потому что
(0,
+∞). Она элементарная, а значит непрерывная
в области существования. Односторонние
пределы неравны, потому что
 =
-π/2,
=
-π/2,
 =
π/2. Это означает, что при х=0 функция
терпит разрыв первого рода.
=
π/2. Это означает, что при х=0 функция
терпит разрыв первого рода.

Задания 3) и4) для самостоятельного решения.
Ответ. 1). х=0 точка разрыва, 2). х=0 точка разрыва, 3). х=0 точка разрыва, 4). х=1 точка разрыва.
-
Найти промежутки непрерывности и классифицировать точки разрыва для следующих функций:
1).
 ;
2).
;
2).
 ;
3).
;
3).
 .
.
Решение.
1).
 .
Функция является элементарной и
определена при х
.
Функция является элементарной и
определена при х (-∞; 0)
(-∞; 0) (0,
+∞), следовательно, на этих интервалах
она непрерывная.
(0,
+∞), следовательно, на этих интервалах
она непрерывная.
Вычислим
односторонние пределы, получим
 =1,
=1,
 =0.
=0.
Значит, х=0 точка разрыва первого рода.
Задания 2) и 3) для самостоятельного решения.
Ответ. 1). х=0 точка разрыва 1 рода, 2). х=2 точка разрыва (устранимого), 3). х=-1 х=1 точки разрыва 2 рода.
-
Исследовать на непрерывность функции
1).
 ;
2).
;
2).
 3).
3).

Решение.
1).
 .
Пусть х<2, тогда f(x)=
-(1/2)x2
является непрерывной на данном множестве.
Если х>2, то f(x)=x
и так же является непрерывной на указанном
множестве. Осталось исследовать точку
х=2. Вычислим односторонние пределы
функции f(x).
Получим
.
Пусть х<2, тогда f(x)=
-(1/2)x2
является непрерывной на данном множестве.
Если х>2, то f(x)=x
и так же является непрерывной на указанном
множестве. Осталось исследовать точку
х=2. Вычислим односторонние пределы
функции f(x).
Получим
 =-2,
=-2,
 =2.
Значит, в точке х=2 функция f(x)
терпит разрыв первого рода.
=2.
Значит, в точке х=2 функция f(x)
терпит разрыв первого рода.

Задания 2) и 3) для самостоятельного решения.
Семинар № 6.4 (19). Вычисление по непрерывным процентам.
Теория.
Известно, что формула сложных процентов
имеет вид
 ,
где Q0
– первоначальная сумма вклада, р –
процент начисления за определенный
период времени (месяц, год), n-
количество периодов времени хранения
вклада, Qn
– сумма вклада по истечении n
периодов времени.
,
где Q0
– первоначальная сумма вклада, р –
процент начисления за определенный
период времени (месяц, год), n-
количество периодов времени хранения
вклада, Qn
– сумма вклада по истечении n
периодов времени.
(Этой формулой можно пользоваться в демографических расчетах, например, прирост населения, и в прогнозах экономики, например, увеличение валового национального продукта).
Пусть р=100% годовых. Составим таблицу расчета Qn.
|
n |
За один промежуток |
|
Примечание |
|
1 |
1 |
|
Процент начисляется один раз в год |
|
2 |
1/2 |
|
Процент начисляется один раз в полугодие |
|
4 |
1/4 |
|
Процент начисляется ежеквартально |
|
12 |
1/12 |
|
Процент начисляется ежемесячно |
|
365 |
1/365 |
|
Процент начисляется ежедневно |
|
8720 |
1/8720 |
|
Процент начисляется ежечасно |
|
n |
1/n |
|
Непрерывное начисление процента |
Сколько
бы ни было велико число начислений n,
годовая сумма накоплений не превзойдет
еQ0,
а доход, который можно получить при
непрерывном начислении процентов, может
составить за год не более, чем
 .
.
В
общем случае, если р – процент начисления
за год разбит на n
частей, то через t
лет сумма депозита достигнет величины
 ,
где r=p/100
– годовая ставка процента. Это выражение
можно преобразовать к виду
,
где r=p/100
– годовая ставка процента. Это выражение
можно преобразовать к виду
 и
и
 при n→∞.
Расчеты, выполненные по этой формуле,
называют вычислениями по непрерывным
процентам.
при n→∞.
Расчеты, выполненные по этой формуле,
называют вычислениями по непрерывным
процентам.
Пример. Пусть темп инфляции составляет 1% в день. На сколько уменьшится первоначальная сумма через полгода?
Решение.
Полгода составляют 182 дня.
 ,
преобразуем, получим
,
преобразуем, получим
 ≈
≈ .
.
Ответ. Приблизительно в 6 раз.


 =2
Q0
=2
Q0 =(3/2)2
Q0=2,25
Q0
=(3/2)2
Q0=2,25
Q0 =2,44
Q0
=2,44
Q0 ≈2,61
Q0
≈2,61
Q0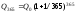 ≈2,714
Q0
≈2,714
Q0 ≈2,718
Q0
≈2,718
Q0 при
n→∞
при
n→∞