
- •230105 «Программное обеспечение вычислительной техники и
- •Зам. Директора по ур
- •Содержание
- •Введение
- •1 Общие положения
- •2. Тематика заданий на курсовую работу
- •3. Выполнение курсовой работы
- •4 Содержание разделов курсовой работы
- •5 Общие требования к оформлению пояснительной записки
- •6 Список рекомендуемой литературы, при выполнении задания курсовой работы
- •Приложение а Методика решения злп симплекс-методом
- •Проверяем выполнение критерия оптимальности при решении задачи на максимум. Наличие в последней стороне отрицательных коэффициентов говорит о том, что решение не оптимально.
- •Приложение б Методика решения транспортной задачи методом потенциалов
- •Алгоритм метода потенциалов.
- •Приложение в Методика решения задачи методом искусственного базиса
- •Первая итерация
- •Вторая итерация
- •Приложение г Методика нахождения максимального потока в графе по алгоритму Форда-Фалкерсона
- •Заключительный шаг
- •Приложение д Методика решения задачи о коммивояжере
- •Приложение а
- •Краткое описание разделов примера курсовой работы
- •Результаты тестирования программы
Алгоритм метода потенциалов.
-
проверяем тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;
-
находим опорный план X0 перевозок путем составления 1-й таблицы одним из способов - северо-западного угла или наименьшего тарифа;
-
проверяем план (таблицу) на удовлетворение системе уравнений и на невырожденность; в случае вырождения плана добавляем условно заполненные клетки с помощью « 0 »;
-
составляем систему уравнений потенциалов по заполненным клеткам. Находим одно из ее решений при u1=0;
-
Строим оценочную матрицу C0=|| Cij- ui - vj ||
-
Проверяем критерий оптимальности. Если в оценочной матрице нет отрицательных значений , то план оптимален (критерий оптимальности). Решение закончено: ответ дается в виде плана перевозок последней таблицы и значения f.
-
Если критерий оптимальности не выполняется, то переходим к выполнению последовательных итераций метода потенциалов, связанных с преобразованием двух матриц C0 и X0:
-
Для перехода к следующей таблице(плану):
а) В оценочной матрице выбираем отрицательный элемент. Если таких клеток несколько, то выбираем с наименьшим значением. Свободная клетка rk, соответствующая этому элементу, подлежит замещению. Элемент Сrk называется особо выделенным
б) В решении X0 составляем цикл пересчета для этой клетки rk и расставляем знаки « + », « - » в вершинах цикла путем их чередования, приписывая пустой клетке « + »;
в) находим число
перерасчета по циклу: число
![]() =min{Xij},
где Xij
- числа в
заполненных клетках X0
со знаком
« - »;
=min{Xij},
где Xij
- числа в
заполненных клетках X0
со знаком
« - »;
г) составляем новую
таблицу, добавляя
![]() в плюсовые клетки и отнимая
в плюсовые клетки и отнимая
![]() из минусовых клеток цикла. Получаем
новое решение X1
из минусовых клеток цикла. Получаем
новое решение X1
д) Подчеркиваем в оценочной матрице C0 элементы, соответствующие занятым в решении X1 клеткам. При этом всегда подчеркиваются нули и один ненулевой элемент Сrk, выделенный в пункте а)
е) Строим цепочку выделения. Она строится от особо выделенного элемента по строкам, затем по столбцам, каждый элемент, попавший в цепочку выделяет и строку и столбец, кроме выделенного элемента. Он выделяет только строку
ж) Прибавляя к выделенным строкам |Сrk |, а из выделенных столбцов вычитая |Сrk|, получим новую оценочную матрицуС1, у которой на всех подчеркнутых местах окажутся нули. Эта матрица будет оценочной для X1
-
Переходим к п. 6
Через конечное число шагов (циклов) обязательно приходим к ответу, ибо транспортная задача всегда имеет решение.
Приложение в Методика решения задачи методом искусственного базиса
В каждое i-ое ограничение вводим искусственную переменную xn+i >0. Всего m новых искусственных переменных.
В целевую функцию F вводим m дополнительных отрицательных слагаемых вида : -M*xn+1 -M*xn+2 ...-M*xn+m , где М - произвольная очень большая константа.
Получим новую задача линейного программирования вида : F(x) = c1х1 + ... + сnxn -M*xn+1 - ... -M*xn+m -------≥ max ai,1x1+ ... + ai,nxn +xn+i = bi , (i=1,m) xj >0 , (j=1,n+m) Новая система ограничений характерна тем, что искусственные переменные сразу можно взять в качестве базисных: xn+i = bi - ai,1x1 - ... - ai,nxn , (i=1,m)
4. Формируем начальное базисное решение новой М-задачи: x' = ( 0, ... 0, b1, ... bm )
5. Решаем М-задачу симплекс-методом
6. Анализируем решение М-задачи в соответствии со следующими
правилами:
-
Если в оптимальном решении М-задачи: x" = ( x"1, ... x"n, x"n+1, ... x"n+m ) все искусственные переменные равны 0, то вектор x" = ( x"1, ... x"n ) является оптимальным решением исходной задача линейного программирования.
-
Если в оптимальном решении М-задачи хотя бы одна искусственная переменная не равна 0, то исходная задача линейного программирования не имеет решения в силу несовместимости ограничений.
-
Если М-задача не имеет решения , то исходная задача линейного программирования также не имеет решения в силу неограниченности целевой функции на допустимом множестве.
Определение исходного опорного плана и исходной симплекс-таблицы, с которой начинаются все итерации.
Пусть поставлена задача линейного программирования
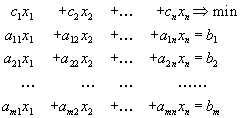
![]() .
.
Можно
считать, что все
![]() ,
так как умножением соответствующего
,
так как умножением соответствующего
ограничения
на -1 у
![]() всегда
можно сменить знак.
всегда
можно сменить знак.
Возьмем очень большое число M и будем решать следующую вспомогательную задачу:
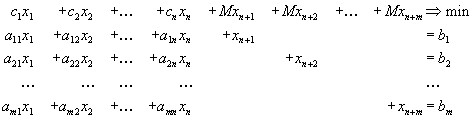
![]()
В качестве исходного опорного плана надо взять план
![]()
![]()
Коэффициенты
разложения векторов
![]() .
Исходная симплекс-таблица приобретает
тогда вид:
.
Исходная симплекс-таблица приобретает
тогда вид:
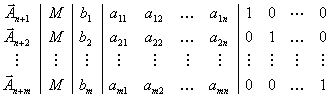 Сформировать
дополнительную строку, где стоят числа
Сформировать
дополнительную строку, где стоят числа
![]() и
и
![]() :
:
![]()
А теперь начнем
преобразования симплекс-таблицы,
стараясь выводить из базиса векторы,
соответствующие введенным дополнительным
переменным. Так как M
очень большое,
то среди разностей
![]() будет
много положительных и будет много
претендентов на введение в базис из
будет
много положительных и будет много
претендентов на введение в базис из
векторов![]() . Заметим,
что если какой-то вектор, соответствующий
какой-то дополнительной переменной
. Заметим,
что если какой-то вектор, соответствующий
какой-то дополнительной переменной
![]() выведен
из базиса, то соответствующий столбец
симплекс-таблицы можно просто вычеркнуть
и больше к нему не возвращаться.
выведен
из базиса, то соответствующий столбец
симплекс-таблицы можно просто вычеркнуть
и больше к нему не возвращаться.
Возможны два варианта.
Все векторы, соответствующие введенным дополнительным переменным, будут выведены из базиса. В этом случае мы просто вернемся к исходной задаче, попав в какую-то вершину допустимой области. Все столбцы симплекс-таблицы, соответствующие дополнительным переменным, тогда исчезнут и дальше будет решаться исходная задача.
Несмотря на то, что M очень велико, получающийся оптимальный план будет все-таки содержать какую-то из дополнительных переменных. Это означает, что допустимая область исходной задачи пуста, то есть ограничения исходной задачи противоречивы и поэтому исходная задача вообще не имеет решений.
Заметим, что величина M вообще не конкретизируется и так и остается в виде буквы M. При решении учебных задач в дополнительную строку пишут алгебраические выражения, содержащие M, а при счете на ЭВМ вводится еще одна дополнительная строка, куда пишутся коэффициенты при M.
Пример
Решить задачу линейного программирования
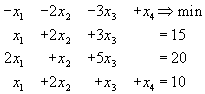
![]()
Заметим,
что у нас уже есть один подходящий вектор
это вектор
![]() при
переменной
при
переменной
![]() .
Поэтому вводим лишь две дополнительные
переменные
.
Поэтому вводим лишь две дополнительные
переменные
![]() ,
заменяя исходную задачу следующей:
,
заменяя исходную задачу следующей:
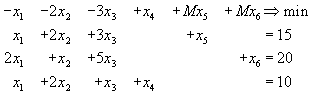
![]()
Исходная симплекс-таблица примет тогда вид:
|
ба- зис |
с
|
план |
-1 |
-2 |
-3 |
1 |
М |
М |
|
|
|
|
|
|
|
|
||
|
|
M |
15 |
1 |
2 |
3 |
0 |
1 |
0 |
|
|
M |
20 |
2 |
1 |
5 |
0 |
0 |
1 |
|
|
1 |
10 |
1 |
2 |
1 |
1 |
0 |
0 |
|
|
|
10+ 35M |
2+ 3M |
4+ 3M |
4+ 8 |
0 |
0 |
0 |


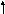 M
M