2. Статистические оценки параметров распределения

Генеральным средним называют среднее арифметическое значений некоторого признака генеральной совокупности. Если все значения различны, то:

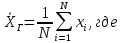
— объём генеральной совокупности.

Выборочным средним называют среднее арифметическое значений некоторого признака выборочной совокупности. Если все значения различны, то выборочная средняя считается по формуле:

— объём выборки.

Выборочная средняя является случайной величиной. Её математическое ожидание равно генеральному среднему:

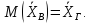
Это означает, что выборочное среднее является несмещённой оценкой генерального.

Генеральной дисперсией называют среднее арифметическое квадрата отклонений признака генеральной совокупности от генерального среднего. Если все значения признака различны, то:

Генеральным средним квадратическим отклонением (стандартом) называется корень квадратный из генеральной дисперсии.

Выборочной дисперсией называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от выборочного среднего. Если все значения признака различны, то:

То есть выборочно дисперсия не является несмещённой оценкой генеральной дисперсии. Поэтому, вместо выборочной дисперсии обычно рассматривают исправленную выборочную дисперсию:

которая является несмещённой оценкой генеральной дисперсии.

Выборочное среднее квадратическое отклонение определяется по формуле:

3. Определение требуемого объёма выборки

Найденная по данным выборки величина 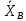представляет собой статистическую оценку неизвестного параметра .

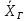Доверительную вероятностью называют вероятность того, что абсолютная величина отклонения оценки от истинного значения не превышает некоторой заданной характеристики точности .

Иначе говоря, есть вероятность того, что интервал заключает в себе истинное значение параметра . Этот интервал называют доверительным.

Если случайная величина имеет нормальное распределение, то для определения математического ожидания выборочного среднего и его среднего квадратического отклонения справедливо соотношение:

Будем считать, что среднее квадратическое отклонение известно, тогда вероятность того, что истинное значение математического ожидания случайной величины будет равно:

Пример:

При каком объёме выборки можно утверждать с надёжностью , что отклонение выборочной средней от генеральной не превысит ошибку , если известна ?

Тема: Теоретические основы имитационного моделирования

Имитационное моделирование — разновидность теоретического моделирования. Этот вид моделирования базируется на компьютерных технологиях. Многие моделирующие системы, идеологически разработанные в 70-80 гг. прошлого века, претерпели эволюцию вместе с компьютерной техникой и оперативными системами. Кроме этого, в 90-х гг. прошлого века, появились принципиально новые моделирующие системы, концепции которых просто не могли появиться раньше.

1. Основы имитационного статистического моделирования

1. Понятие модели

Модель — объект любой природы, который создаётся исследователем с целью получения новых знаний об объекте-оригинале и отражает только существенное (с точки зрения разработчика) свойства оригинала. Из этого следует, что любая модель субъективна, то есть несёт на себе печать индивидуальности исследователя; Модель – объект любой природы, который создаётся исследователем с целью получения новых знаний об объекте-оригинале и отражает только существенное (с точки зрения разработчика) свойства оригинала. Из этого определения следует, что любая модель субъективна, то есть несёт на себе печать индивидуальности исследователя; любая модель гомоморфна, т.е. в ней отражаются не все, а только существенные свойства оригинала; возможно существования множества объектов одного и того же объекта оригинала, отличающихся целями исследования и степенью адекватности. Модель считается адекватной если она с достаточной степенью приближения на уровне понимания моделируемого процесса исследователем отражает закономерности процесса функционирования реальной системы во внешней среде.