Свойства функции распределения

1. Значения при изменении от до лежат в промежутке от 0 до 1;

2. — неубывающая функция;

3. Имеет место равенство ;

4. Вероятность попадания случайной величины в интервал находится по формуле: .

Из свойств функции распределения вытекают свойства функции плотности распределения вероятности.

Свойства функции плотности распределения вероятности

1. Функция всегда неотрицательна;

2. Интеграл от по всей оси равна 1. Таким образом, площадь фигуры под графиком функции всегда равна 1;

3. Вероятность попадания случайной величины 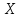в произвольный интервал равна .

2. Числовые характеристики непрерывных случайных величин

Функция распределения или плотность распределения полностью определяют непрерывную случайную величину; однако, случайная величина может быть задана ещё и несколькими числовыми характеристиками, к которым прежде всего относятся математическое ожидание и дисперсия.

Математическим ожиданием или средним значением непрерывной случайной величины называется число, определяемое по формуле:

Дисперсией непрерывной случайной величины называется математическое ожидание квадрата отклонения от среднего значения:

Арифметическое значение называется средним квадратическим отклонением:

Свойства математического ожидания

1. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:

2. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю;

2. Дисперсия суммы или разности двух независимых случайных величин равна сумме их дисперсий:

3. Распределения непрерывных случайных величин

Наиболее распространёнными являются следующие распределения случайных величин:

• Равномерное распределение;

• Показательное распределение (экспоненциальное);

• Нормальное распределение.

Равномерное распределение

Непрерывная случайная величина , принимающая значения в интервале имеет равномерное распределение, если плотность распределения имеет вид:

Функция распределения этой случайной величины:

Числовые характеристики этой случайной величины: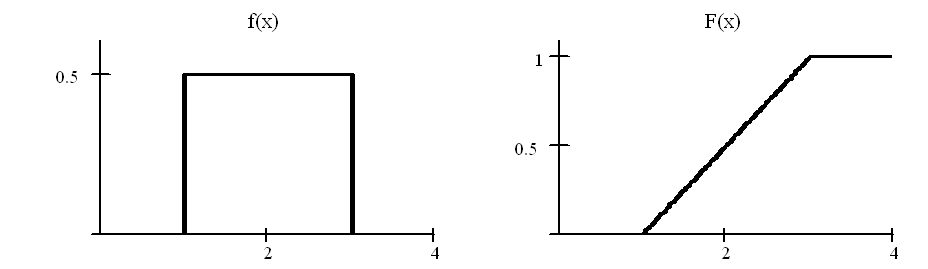

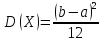
Показательное распределение

Непрерывная случайная величина, принимающая неотрицательные значения, имеет показательное распределение, если плотность распределения имеет вид:

— постоянная положительная величина.

Функция распределения в этом случае имеет вид:

Числовые характеристики этой случайной величины:

Нормальное распределение (распределение Гаусса)

Нормальным распределением называется распределение случайной величины, функция плотности распределения которой имеет вид:

— математическое ожидание, а — среднее квадратическое отклонение.

Функция распределения определяется по формуле:

Введём нормированную и центрированную случайную величину с нормальным распределением:

вместо . Для неё составлена табличная функция Лапласа, имеющая вид:

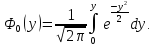
С помощью табличной функции Лапласа можно определить вероятность попадания случайной величины в интервал :