Xlabel('X') % метка оси ox

ylabel('y(x)') % метка оси OY

Leg = diff(dFdy1,Dy) % F_y'y' - достаточное условие Лежандра

Leg =

2

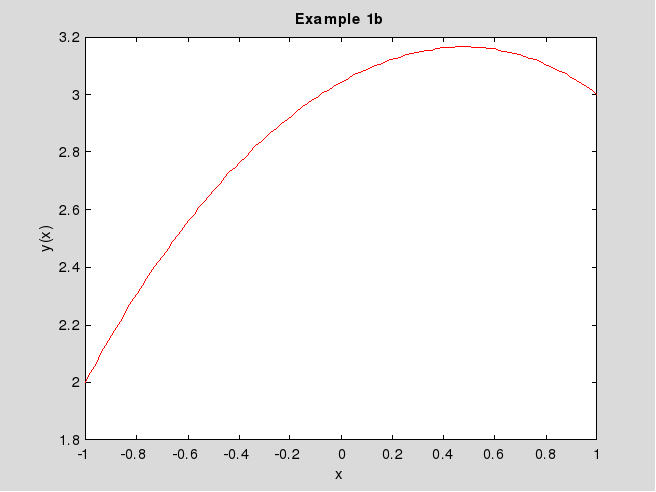
Рис. 1.2. Решение примера 1b

Ответ. Первый интеграл дифференциального уравнения Эйлера

. (1.0)

Экстремаль функционала (1.11) имеет вид

. (1.0)

График её показан на рис.1.2. Так как F_y’y’2>0, и это выполняется y(x) и y(x), то по достаточному условию Лежандра имеем сильный минимум.

3. Пример 1c

Найти экстремаль функционала

(1.0)

Исследовать на достаточные условия. Построить график решения.

Здесь подынтегральная функция F(x,y,y) не зависит явно от x. Первый интеграл уравнения Эйлера имеет вид FyF_yC₁. Составим программу для решения этого примера. Вначале введём исходные данные задачи.

clear all % очищаем память

format long % формат отображения чисел с 14 знаками

disp('Решаем пример 1c') % печатаем заголовок

syms x y Dy % описали символические переменные

F=y^2*Dy^2; % вводим подынтегральную функцию

x1=1;

y1=4;

x2=3;

y2=3;

fprintf('Подынтегральная функция: F=%s\n',char(F))

fprintf('Граничные условия: y(%d)=%d; y(%d)=%d\n',x1,y1,x2,y2)

Решаем пример 1c

Подынтегральная функция: F=y^2*Dy^2

Граничные условия: y(1)=4; y(3)=3

Выводим первый интеграл уравнения Эйлера. Решаем полученное уравнение.

dFdy1 = diff(F,Dy) % F_y'

Euler=simple(F-Dy*dFdy1) % левая часть уравнения Эйлера

deqEuler = [char(Euler) '=C'] % составили уравнение

Sol = dsolve(deqEuler,'x') % решаем уравнение Эйлера

if length(Sol)~=1 % решений нет или более одного

error('Нет решений или более одного решения!');

end

dFdy1 =

2*y^2*Dy

Euler =

-y^2*Dy^2

deqEuler =

-y^2*Dy^2=C

Sol =

[ (-2*(-C)^(1/2)*x+C1)^(1/2)]

[ -(-2*(-C)^(1/2)*x+C1)^(1/2)]

[ (2*(-C)^(1/2)*x+C1)^(1/2)]

[ -(2*(-C)^(1/2)*x+C1)^(1/2)]

??? Нет решений или более одного решения!

Первая проблема! Решение данной задачи – не единственное. MATLAB не смог упростить первый интеграл уравнения Эйлера, и оставил его в виде: y²y²=C. Нам прийдётся упростить его вручную.

Euler = y*Dy % упрощаем вручную

deqEuler = [char(Euler) '=C'] % составили уравнение

Sol = dsolve(deqEuler,'x') % решаем уравнение Эйлера

if length(Sol)~=1 % решений нет или более одного

error('Нет решений или более одного решения!');

end

Euler =

y*Dy

deqEuler =

y*Dy=C

Sol =

[ (2*C*x+C1)^(1/2)]

[ -(2*C*x+C1)^(1/2)]

??? Нет решений или более одного решения!

Уравнение упростилось, но оно по-прежнему имеет более одного решения. Для удовлетворения заданным граничным условиям мы должны выбрать первое решение. Выбираем его, и повторяем далее все операторы программы примера 1a.

SolLeft = subs(Sol(1),x,sym(x1)) % подставляем x1 в первое решение

SolRight = subs(Sol(1),x,sym(x2)) % подставляем x2 в первое решение

EqLeft = [char(SolLeft) '=' char(sym(y1))] % приравниваем y1

EqRight = [char(SolRight) '=' char(sym(y2))] % приравниваем y1

Con=solve(EqLeft,EqRight); % решаем систему уравнений

C=Con.C % присвоили полученные решения

C1=Con.C1 % символическим переменным C и C1

Sol1c = vpa(eval(Sol(1)),14); % подставляем C1, C2 в решение с 14 знаками

fprintf('Уравнение экстремали:\n%s\n',char(Sol1c))

xpl=linspace(x1,x2); % задаём массив абсцисс

y1c=subs(Sol1c,x,xpl); % вычисляем ординаты

plot ( xpl, y1c, '-r' ) % рисуем график функции

title ( '\bfExample 1c' ) % заголовок