Xlabel('X') % метка оси ox

ylabel('y(x)') % метка оси OY

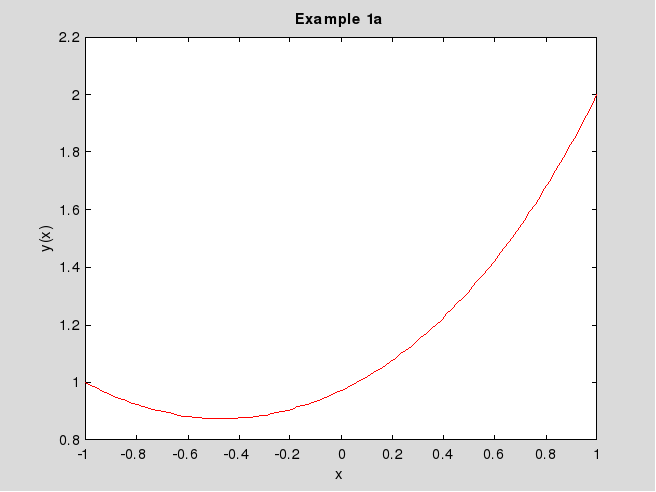
Рис. 1.1. Решение примера 1a

Ответ. Уравнение Эйлера после сокращения на –2 будет:

. (1.0)

Его аналитическое решение

. (1.0)

После подстановки значений произвольных постоянных экстремаль функционала (1.6) имеет вид

. (1.0)

График её показан на рис.1.1. Так как F_yy2>0, и это условие выполняется y(x) и y(x), то в соответствии с достаточным условием Лежандра найденная экстремаль доставляет сильный минимум функционалу (1.6).

2. Пример 1b

Найти экстремаль функционала

(1.0)

Исследовать на выполнение достаточных условий экстремума. Построить график решения.

В этом примере подынтегральная функция F(x,y,y) не зависит явно от y. Первый интеграл уравнения Эйлера имеет вид F_yC₁. Составим программу для решения этой вариационной задачи. Вначале введём исходные данные.

clear all % очищаем память

format long % формат отображения чисел с 14 знаками

disp('Решаем пример 1b') % выводим заголовок задачи

syms x Dy % описали символические переменные

F=Dy^2+2*Dy*sinh(x)-5*x^2; % вводим подынтегральную функцию

x1=-1; % вводим граничные условия

y1=2;

x2=1;

y2=3;

fprintf('Подынтегральная функция: F=%s\n',char(F))

fprintf('Граничные условия: y(%d)=%d; y(%d)=%d\n',x1,y1,x2,y2)

Решаем пример 1b

Подынтегральная функция: F=Dy^2+2*Dy*sinh(x)-5*x^2

Граничные условия: y(-1)=2; y(1)=3

У нас будет первый интеграл уравнения Эйлера, поэтому ни сама функция y, ни её вторая производная y нам не нужны, и мы их не описываем. Строим первый интеграл и решаем полученное дифференциальное уравнение. Названия констант C1 и C2 используются в команде dsolve, поэтому обозначим константу C.

dFdy1 = simple(diff(F,Dy)) % F_y'

deqEuler = [char(dFdy1) '=C'] % составили уравнение

Sol = dsolve(deqEuler,'x') % решаем уравнение Эйлера

if length(Sol)~=1 % решений нет или более одного

error('Нет решений или более одного решения!');

end

dFdy1 =

2*Dy+2*sinh(x)

deqEuler =

2*Dy+2*sinh(x)=C

Sol =

-cosh(x)+1/2*C*x+C1

В переменной Sol получено общее решение, произвольные постоянные обозначены C и C1. Найдём их. Для этого подставим в Sol граничные точки.

SolLeft = subs(Sol,x,sym(x1)) % подставляем x1

SolRight = subs(Sol,x,sym(x2)) % подставляем x2

SolLeft =

-cosh(1)-1/2*C+C1

SolRight =

-cosh(1)+1/2*C+C1

Приравняем полученные выражения соответственно y1 и y2. Тем самым мы сформируем систему алгебраических уравнений. Решим её. Подставим найденные константы C и C1 в решение Sol.

EqLeft = [char(SolLeft) '=' char(sym(y1))] % приравняли y1

EqRight = [char(SolRight) '=' char(sym(y2))] % приравняли y2

Con = solve(EqLeft,EqRight); % решаем систему уравнений

C=Con.C % присвоили полученные решения

C1=Con.C1 % символическим переменным C и C1

Sol1b = vpa(eval(Sol),14); % подставляем C1, C в решение с точностью 14 знаков

fprintf('Уравнение экстремали:\n%s\n',char(Sol1b))

EqLeft =

-cosh(1)-1/2*C+C1=2

EqRight =

-cosh(1)+1/2*C+C1=3

C =

1

C1 =

cosh(1)+5/2

Уравнение экстремали:

-1.*cosh(x)+.50000000000000*x+4.0430806348152

Дальнейшие действия не отличаются от описанных в примере 1a. Рисуем график и проверяем выполнение достаточных условий экстремума.

xpl = linspace(x1,x2); % массив абсцисс

y1b = subs(Sol1b,x,xpl); % вычисляем ординаты

plot ( xpl, y1b, '-r' ) % рисуем график

title ( '\bfExample 1b' ) % заголовок