
Переход к другой системе отсчёта
Пусть
К и К′ - произвольные системы отсчёта.
Скорость
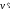 и ускорение
и ускорение
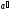 точки в СО
точки в СО
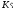 известны.
Найти
известны.
Найти
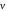 и
и
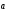 точки в К.
точки в К.
Случай
1:
К′ движется поступательно в К. Начало
отсчёта
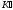 т.О′ характеризуется в К радиус –
вектором
т.О′ характеризуется в К радиус –
вектором
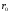 ,
а её скорость и ускорение
,
а её скорость и ускорение
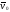 и
и
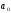 .
Положение т.А в К определяет радиус –
вектор
.
Положение т.А в К определяет радиус –
вектор
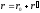 .
За время dt
т.А совершит в СО К перемещение
.
За время dt
т.А совершит в СО К перемещение
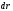 .
Из
.
Из
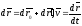 и
и
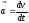 =>
=>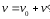 и
и
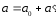 .
.
Случай
2 :
К′ вращается с
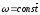 вокруг оси, неподвижной в К.
вокруг оси, неподвижной в К.
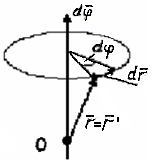
Совместим
начало отсчёта К и К′ в произвольной
т.О на оси вращения. Тогда радиус –
вектор т. А в обеих системах
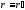 .
.
1)
т. А неподвижна в К′,
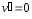 ,
,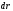 в К за время dt
обусловлено только поворотом К′ в К,
т.е.
в К за время dt
обусловлено только поворотом К′ в К,
т.е.
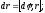
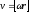 ;
;
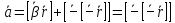 т.к.
т.к.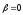
2)
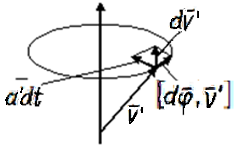
т. А движется в K’
со скоростью
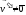 .
За dt
она совершит:
.
За dt
она совершит:
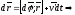
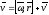 .
Перейдем к ускорениям :
.
Перейдем к ускорениям :
в
К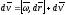 ,
где
,
где
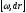 обусловлено
поворотом К´ в К, а
обусловлено
поворотом К´ в К, а
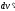 -
изменением
-
изменением
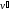 в
К.
в
К.
Найдем
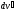 (в
К)
(в
К)
а)
в К’
 (в К) обусловлено только поворотом К’
в К и (по аналогии с
(в К) обусловлено только поворотом К’
в К и (по аналогии с
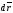 )
)
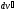 =
=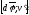 .
Тогда
.
Тогда
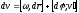 и
и
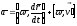 .
С учетом
.
С учетом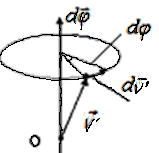
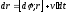 ,
,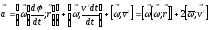 .
.
б)
в К’
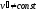 (
(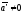 ).
Тогда в К
).
Тогда в К
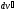 =
=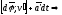 (
с учетом
(
с учетом
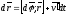 )
)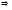
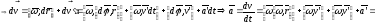
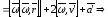
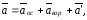
где
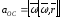 - осестремительное
ускорение;
- осестремительное
ускорение;
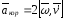 -
ускорение
Кориолиса
(поворотное);
-
ускорение
Кориолиса
(поворотное);
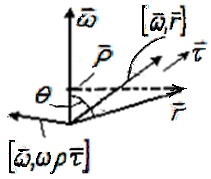
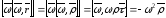 ,
где
,
где
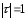 и
и
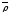 -
радиус-вектор т. А относительно оси
вращения К’ в К и перпендикулярный
этой оси.
-
радиус-вектор т. А относительно оси
вращения К’ в К и перпендикулярный
этой оси.
Тогда
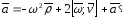

Случай
3: K’
вращается с
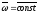 вокруг оси, движущейся в К с
вокруг оси, движущейся в К с
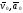 (объединяет случаи 1 и 2).
(объединяет случаи 1 и 2).
Введем вспомогательную систему S, жестко связанную с осью вращения K’.
Пусть
скорость т.А в К и S
системах будет
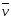 и
и
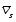 .
Тогда из
.
Тогда из
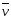 =
=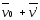 (слу-
(слу-
чай
1)
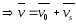 .
Из
.
Из
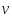 =
=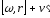 (случай 2)
(случай 2) ,
где
,
где
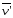 -
скорость т. А в К’;
-
скорость т. А в К’;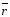 - радиус-вектор, проведенный из произвольной
точки оси вращения в т.А.
- радиус-вектор, проведенный из произвольной
точки оси вращения в т.А.
Тогда
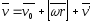 .
Аналогично
для
.
Аналогично
для
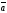 :
:
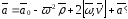 , где
, где
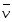 ,
,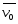 ,
,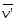 - скорости т. А в К, К’ в К и т. А в К’
соответственно;
- скорости т. А в К, К’ в К и т. А в К’
соответственно;
