
Поступательное движение
Поступательное движение ТТ– движение, при котором любая прямая, связанная с
телом остаётся параллельной своему начальному положению.
При поступательном движении ТТ перемещения, скорости и ускорения всех его точек равны. Значит, описание поступательного движения ТТ сводится к описанию движения любой его точки.
Вращение вокруг неподвижной оси
Пусть ТТ вращается вокруг неподвижной оси Z. Произвольная т.А тела за бесконечно малое время dt повернётся на бесконечно малый угол dφ.
Угол поворота (угловой путь) (φ) – угол между радиусами, проведёнными из центра
обращения точки в её начальное и конечное положения. [φ]= 1 рад.
-
В общем случае
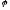 и
и
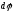 - величины алгебраические (их знак
зависит от направления отсчета).
- величины алгебраические (их знак
зависит от направления отсчета).
Пусть
положительное направление отсчёта φ
связано с направлением Z
правилом правого винта. Угол dφ
характеризуем вектором
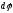 ,
причём |
,
причём |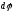 |=
|=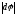 и направление
и направление
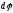 связанно с направлением вращения тела
правилом правого винта.
связанно с направлением вращения тела
правилом правого винта.
Аксиальный вектор – вектор, направление которого связано с направлением
вращения
тела.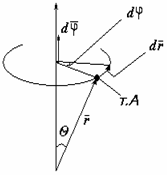
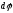 -
аксиальный вектор. Тогда |
-
аксиальный вектор. Тогда |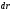 |
=
|
=
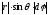 или
или
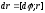 (1)
(1)
-
В виде векторов можно представлять только бесконечно
малые углы поворота.
-
 в
проекции на Z
дает алгебраическую величину
в
проекции на Z
дает алгебраическую величину
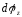 =
=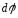 .
.
z
Средняя угловая скорость (ωср) – отношение угла поворота
∆φ ко времени его совершения Δt.
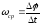 ;
;
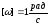
Мгновенная угловая скорость (угловая скорость) (ω) – предел средней угловой
скорости при стремлении к нулю промежутка времени Δt.
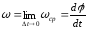 -
алгебраическая величина. ω можно
характеризовать
-
алгебраическая величина. ω можно
характеризовать
аксиальным
вектором
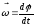 ,
причём |
,
причём |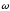 |=|ω|
и
|=|ω|
и
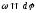 .
.
-
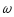 в
проекции на Z
дает алгебраическую величину
в
проекции на Z
дает алгебраическую величину
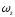 =
=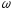 .
.
Среднее угловое ускорение (βср) – отношение изменения Δω угловой скорости ко
времени Δt , в течении которого оно произошло.
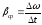 ;
;
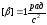 .
.
Мгновенное угловое ускорение (угловое ускорение) (β) – предел среднего
углового ускорения при стремлении к нулю промежутка времени Δt.
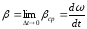 -
алгебраическая величина.
-
алгебраическая величина.
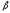 можно характеризовать аксиальным
вектором
можно характеризовать аксиальным
вектором
 ,
причём
,
причём
 =|β|
и
=|β|
и
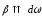 .
.
-
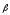 в
проекции на Z
дает алгебраическую величину
в
проекции на Z
дает алгебраическую величину
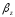 =
=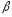 .
.
Итак: зная φ(t) можно найти ω(t) и β(t).
Обратная задача: при β(t) = const найти ω(t) и φ(t) :
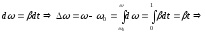
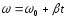 ,
т.е. надо знать ω0.
,
т.е. надо знать ω0.
-
В векторном виде
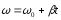
Аналогично
dφ
= ωdt
=>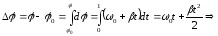
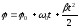 ,
т.е. задача
решаема только при известных начальных
условиях
φ0
и ω0.
По аналогии с векторным способом
,
т.е. задача
решаема только при известных начальных
условиях
φ0
и ω0.
По аналогии с векторным способом
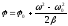 .
.
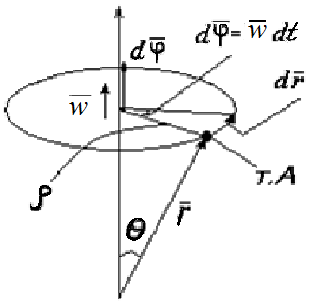
Связь линейных и угловых величин
Из
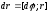 и
и
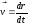 =>
=>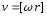
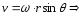
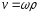 -
алгебраическая величина, где
-
алгебраическая величина, где
ρ – радиус кривизны траектории в т.А
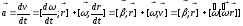 или
или
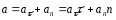 ,
где
,
где
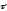 и
и
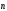 - орты касательной и нормали к траектории
в
- орты касательной и нормали к траектории
в
т.
А, причем
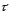 направлен
в сторону увеличения
направлен
в сторону увеличения
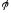 ,
а
,
а
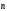 -
к оси Z.
-
к оси Z.

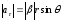 =>
=>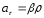 - величина алгебраическая;
- величина алгебраическая;
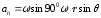 =>
=>
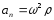 .
.
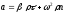 ,
,
 =>
=>
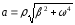 .
.
-
При вращении ТТ вокруг оси Z угловые характеристики движения (φ,ԝ,β ) одинаковы для всех точек, поэтому описание движения ТТ сводится к описанию движения любой его точки (не лежащей на оси ).
