
Координатный способ
Система отсчета (СО) - совокупность, включающая в себя часы, тело отсчета и
жестко связанную с ним систему координат.
Пусть
радиус –вектор
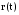 характеризует положение т.А t
и его проекции на оси координат в системе
отсчета OXYZt
:
характеризует положение т.А t
и его проекции на оси координат в системе
отсчета OXYZt
:
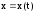 ;
;
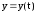 ;
;
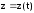 .
.
Тогда
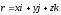 и
и
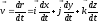 или
или
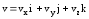 ,
где
,
где
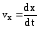 ;
;
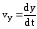 ;
;
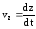 -
проекции
-
проекции
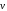 на X,Y,Z;
на X,Y,Z;
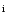 ,
,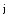 ,
,
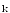 - орты осей X,Y,Z.
- орты осей X,Y,Z.
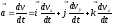 или
или
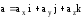 ,
где
,
где
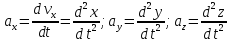 -
проекции
-
проекции
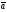 на
X,Y,Z.
на
X,Y,Z.
Длины
векторов
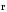 ,
,
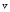 ,
,
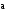 :
:
 ,
,
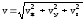 ,
,
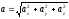 .
.
Направляющие
косинусы: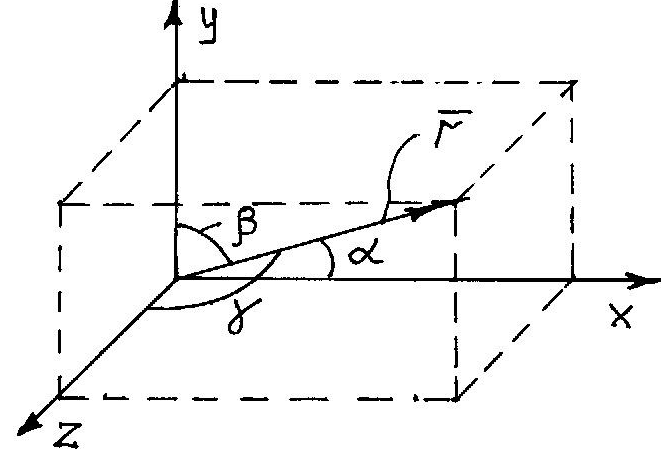
для
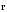 :
:
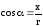 ;
;
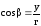 ;
;
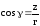 ;
;
для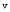 :
:
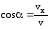 ;
;
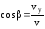 ;
;
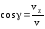 ;
;
для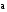 :
:
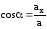 ;
;
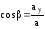 ;
;
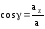 ;
;
По
аналогии с векторным способом обратная
задача (при
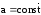 ,т.е.
при постоянных
,т.е.
при постоянных
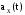 ,
,
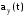 ,
,
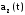 найти
найти
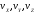 и x,
y,
z)
решаема только при известных
и x,
y,
z)
решаема только при известных
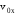 ,
,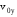 ,
,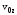 и
и
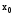 ,
,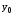 ,
,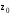 .
.
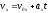 ;
;
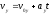 ;
;
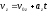
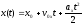 ,
,
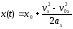 (см. векторный способ), для
(см. векторный способ), для
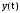 и z(t)
– аналогично.
и z(t)
– аналогично.
Естественный способ
Применяют, когда траектория точки известна.
1)
Описание с помощью дуговой
координаты
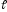 .
.
Дуговая
координата (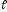 )
– координата, отсчитанная вдоль
траектории от начала
)
– координата, отсчитанная вдоль
траектории от начала
отсчета до текущего положения точки.
-
Начало отсчета и положительное направление отсчета l выбирают произвольно.
Движение точки определено, если известны:
а) траектория;
б) начало отсчета и положительное направление отсчета дуговой координаты;
в)
закон движения точки
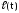
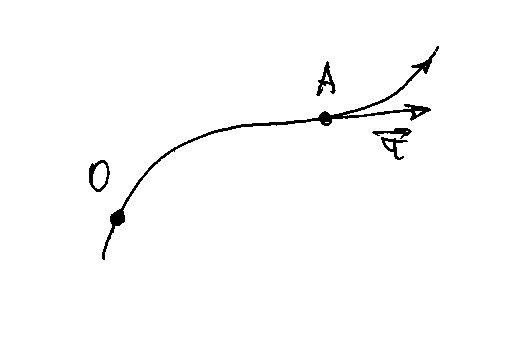
Введем
единичный вектор
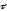 ,
связанный с движущейся точкой А и
направленный по касательной к траектории
в сторону возрастания дуговой координаты
,
связанный с движущейся точкой А и
направленный по касательной к траектории
в сторону возрастания дуговой координаты
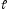 .
Тогда
.
Тогда
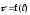 и
и
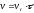 ,
где
,
где
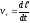 - проекция
- проекция
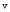 на
направление
на
направление
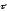 (величина
алгебраическая)
(величина
алгебраическая)
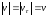 .
.
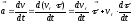 .
При
.
При
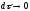
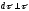 .
Введем единичный вектор
.
Введем единичный вектор
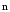 нормали
к траектории в точке 1, тогда
нормали
к траектории в точке 1, тогда
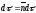 и
и
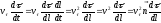 .
.

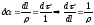 .
Тогда
.
Тогда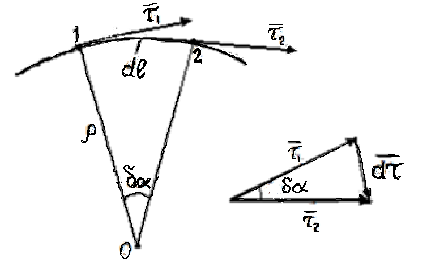
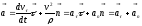 ,
где
,
где
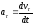 ;
;
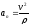
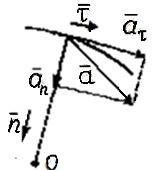
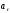 -
тангенциальное
ускорение
(характеризует изменение
-
тангенциальное
ускорение
(характеризует изменение
скорости по модулю).
 -
нормальное
ускорение
(характеризует изменение
-
нормальное
ускорение
(характеризует изменение
скорости по направлению).
-
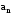 направлено
к центру кривизны траектории в данной
точке , поэтому его называют
центростремительным.
направлено
к центру кривизны траектории в данной
точке , поэтому его называют
центростремительным.
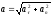
-
Частные случаи движения: а)равномерное прямолинейное
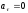 ;
;
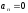 (ρ→∞).
(ρ→∞).
б)равноускоренное
прямолинейное
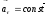 ;
;
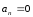 .
.
2) Описание с помощью понятия пути S (частный случай варианта 1 ).
Путь (S) – расстояние между начальным и конечным положениями точки, отсчитанное вдоль траектории.
-
Принимают S0=0 при t0=0 и dS=|dl|.
Тогда
мгновенная путевая скорость
-
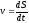
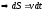 .
.
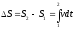 и
средняя
путевая скорость
-
и
средняя
путевая скорость
-
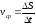 .
.
-
Средняя и мгновенная путевые скорости всегда неотрицательные .
Кинематика твёрдого тела
Твёрдое тело (или абсолютно твёрдое тело) (ТТ) – тело, расстояние между
частицами которого неизменно.
Доказано, что все виды движения ТТ можно представить как совокупность поступательного и вращательного движений.
