Лекция № 4. Смо с отказами и ожиданием
1. Критерии эффективности смо с отказами
Рассмотрим СМО с
n каналами. Входной
поток заявок – простейший, с интенсивностью
.
Выходной поток – простейший. Среднее
время обслуживания заявки одним каналом
–
,
следовательно, время обслуживания
распределено по показательному закону
с функцией распределения
.
Система с отказами, т. е., если все каналы
заняты, заявка покидает систему.
Требуется найти предельные вероятности состояний и характеристики эффективности системы.
Решение:
Состояния:
– все каналы свободны,
– одни канал занят, …,
–
n каналов занято.
Граф состояний – граф «гибели и
размножения».
Рис. 8
Каналы загружаются
под действием потока интенсивности
.
Интенсивность потока
,
т. к. задействованы 2 канала,
и т. д. Здесь
По формулам (3) получим:
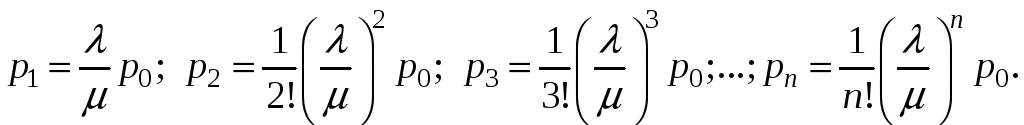
Обозначим
через
и назовем
относительной плотностью потоков.
Получим следующие формулы Эрланга:
.
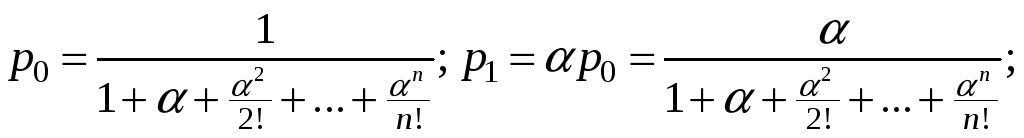
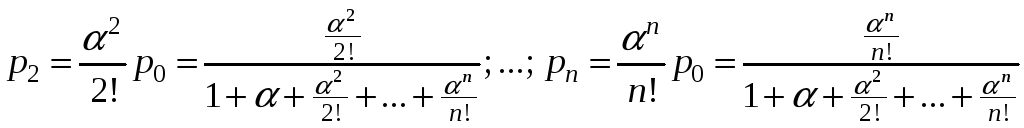(1)
Характеристики эффективности:
1).
;
2).
;
3). Абсолютная пропускная способность (среднее число обслуживаемых заявок в единицу времени):
;
4). Среднее число занятых каналов =
=
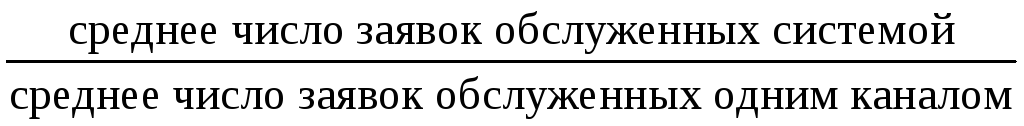
5). Вероятность
загрузки канала
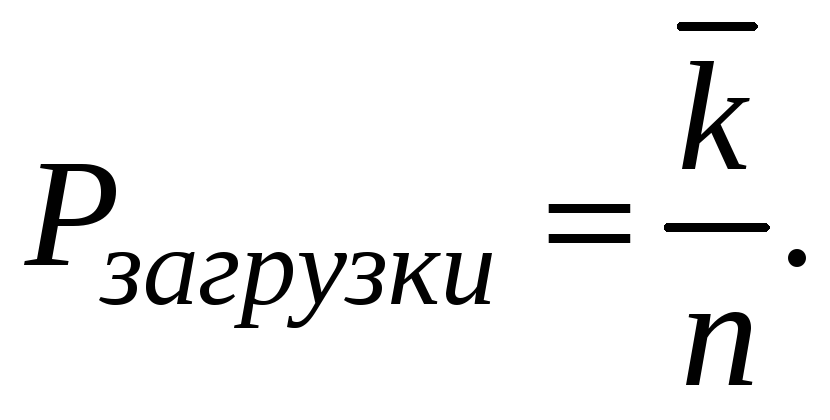
Пример. Станция
наведения состоит из n
каналов. Среднее время наведения
равно
.
Поток заявок – простейший: 4 заявки/мин.
Какое наименьшее число каналов нужно,
чтобы вероятность наведения была больше
90 %? Найти характеристики эффективности.
Решение.
1 канал:
2 канала (n
= 2):
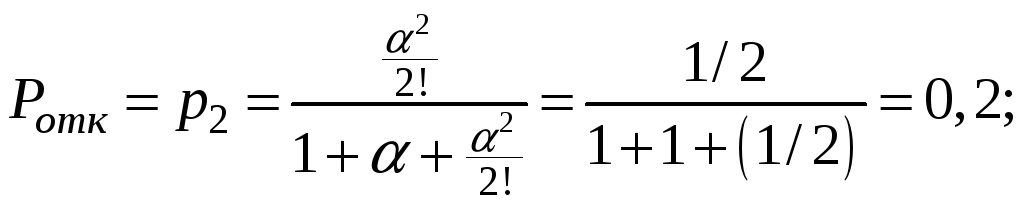
3 канала (n = 3):
,
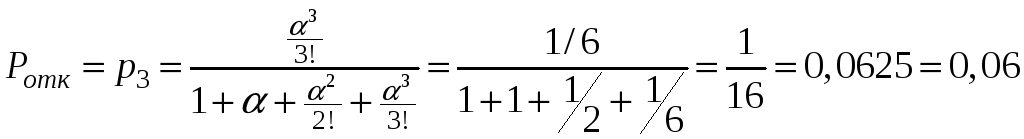заявки/мин,
.
2. Смо с ограниченной и неограниченной очередью
Рассмотрим СМО с
n каналами. Входной
поток – простейший с интенсивностью
.
Выходной поток – простейший. Интенсивность
потока заявок, обслуживаемых одним
каналом, равна
.
Если все каналы заняты, заявка становится
в очередь. Число мест в очереди равно
m. Состояние системы:
– все каналы свободны, очереди нет;
– одни канал занят, очереди нет; …,
– n каналов занято,
очереди нет;
– заняты все каналы и одно место в
очереди, …,
– заняты все каналы и все места в очереди.
Граф состояний (рис. 9).
Рис. 9.
Переходы
возможны только, если освободится канал,
причем задействованы все n
каналов. Поэтому интенсивности каждого
из потоков
равны
.
Пусть
По формулам (3), т. к.
получим:
.
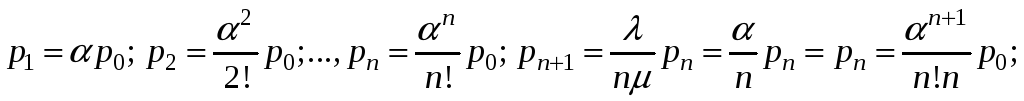
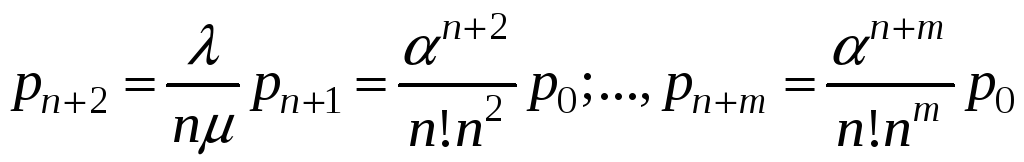Справедливы формулы:
.
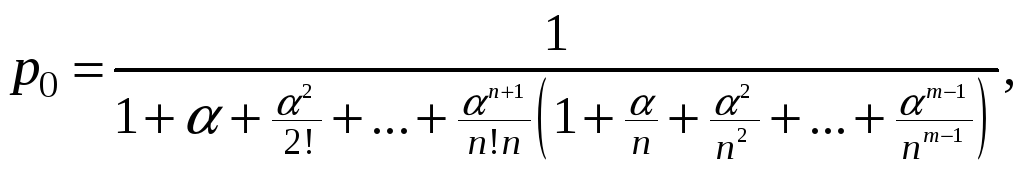
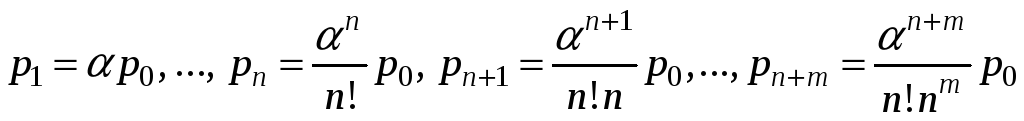(2)
Характеристики эффективности:
1).
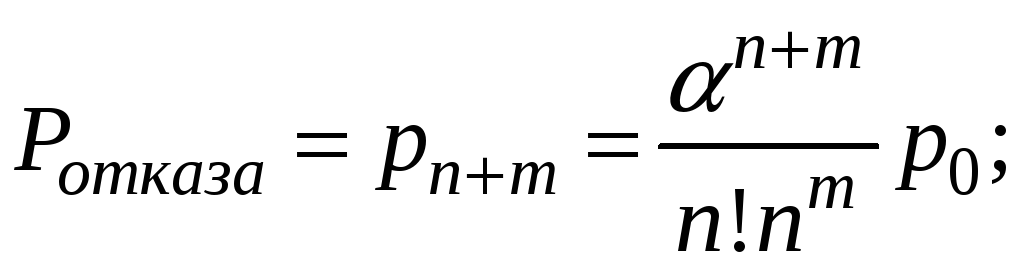
2).
3).
4).
5).
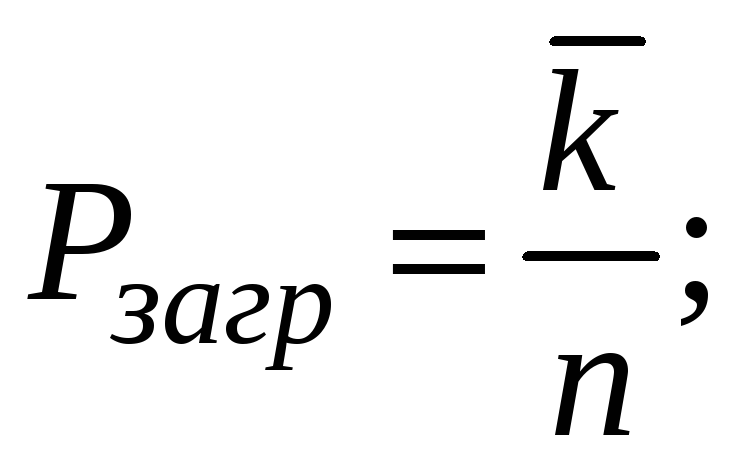
6). Среднее число
занятых мест в очереди
.
Рассмотрим ряд распределения занятых мест в очереди:
-
r
0
1
2
…
M
p
…
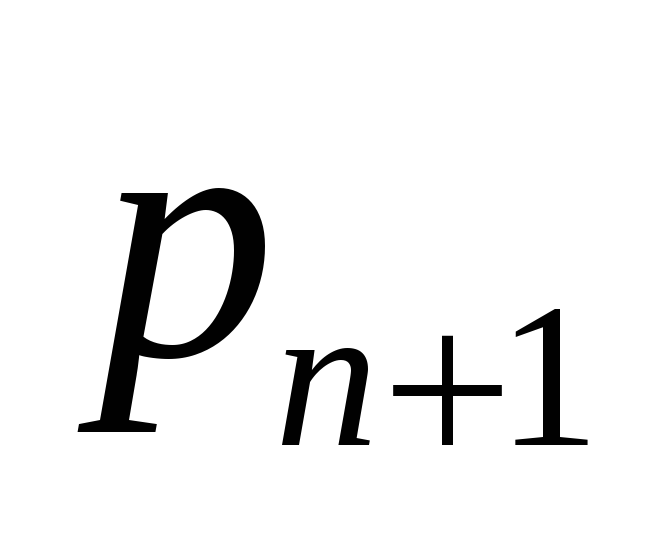
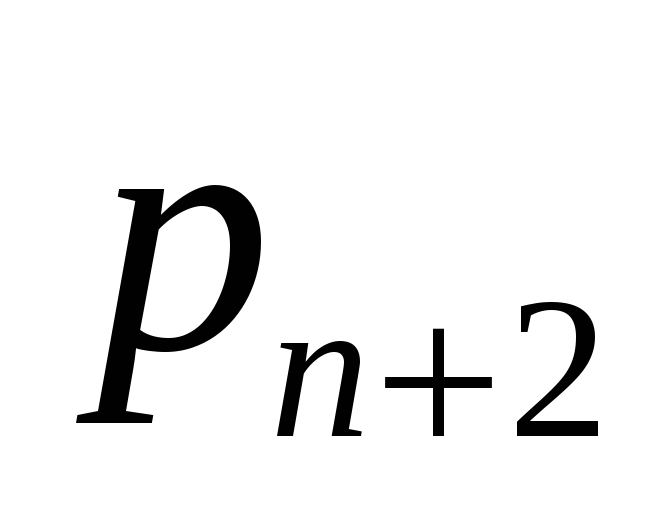
Отсюда следует
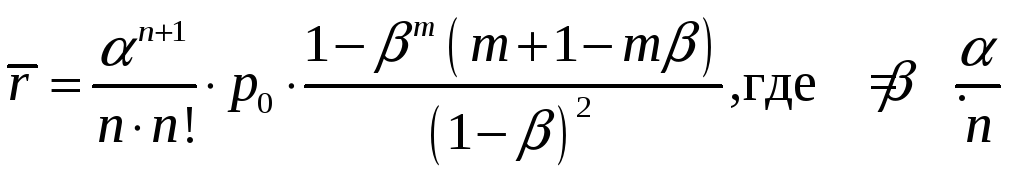
Пример. СМО – аэродром с двумя посадочными полосами. Входной поток – простейший с интенсивностью 2 самолета/час. Среднее время посадки 15 минут. Если полоса занята, 1 самолет может ожидать посадки в зоне аэропорта. Найти предельные вероятности и характеристики эффективности.
Решение.
Состояния системы:
– все полосы свободны;
–
одна полоса занята;
– 2 полосы заняты;
– 2 полосы заняты, 1 самолет ожидает. СМО
с ожиданием:
Рис. 10
По формулам (2) получим:
;
.
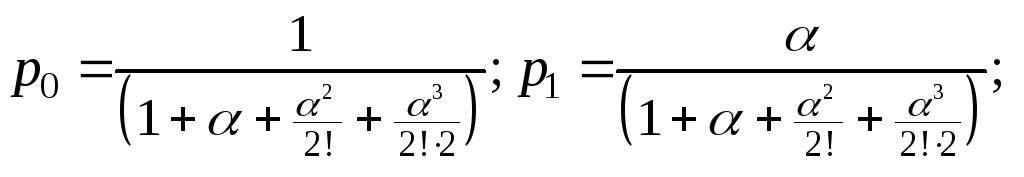
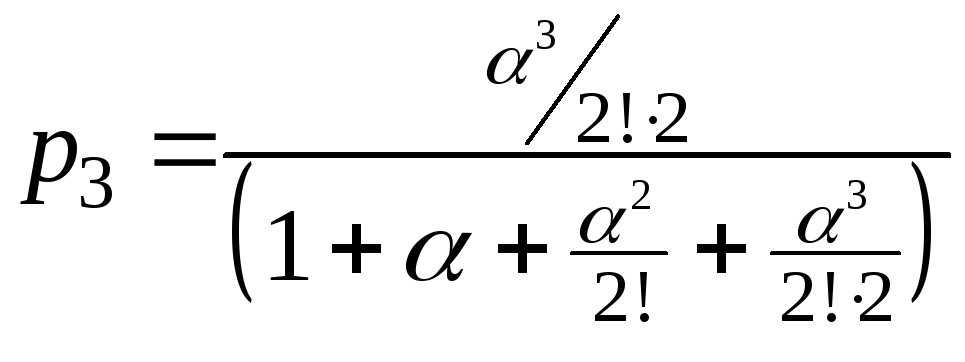1).
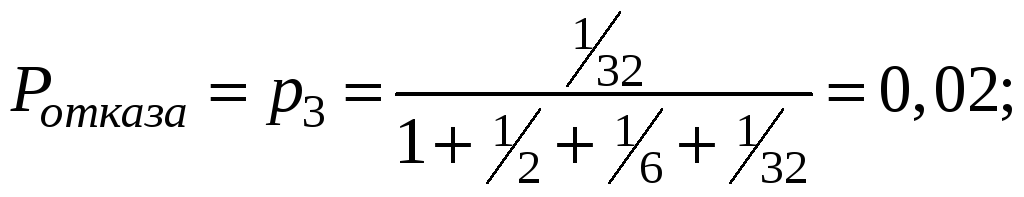2).
3).
4).
5).
6).
Для систем с
неограниченной очередью очень
важным является вопрос, будет ли очередь
лавинообразно нарастать. Для ответа на
него в формулах (2) перейдем к пределу
при
.
В частности, рассмотрим вероятность
:
.
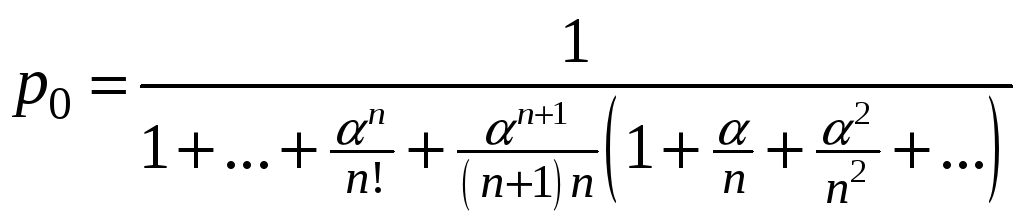Если
,
ряд в знаменателе сходится, и следовательно,
предельные вероятности существуют.
Если
,
то стационарного режима нет:
(входной поток больше, чем максимально
могут обслужить n
каналов). Очередь лавинообразно
нарастает.