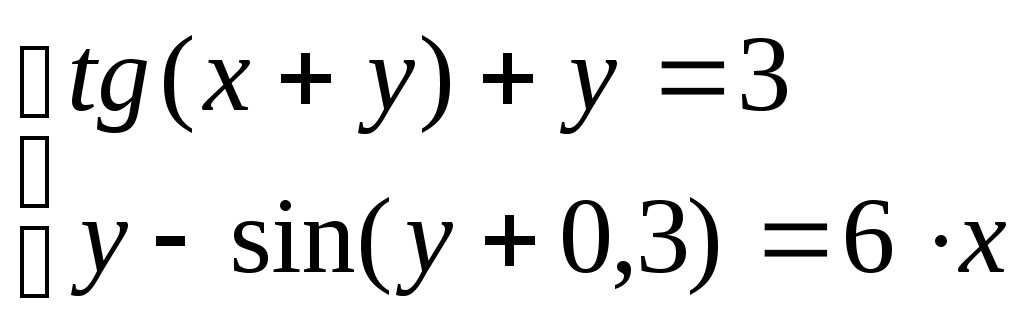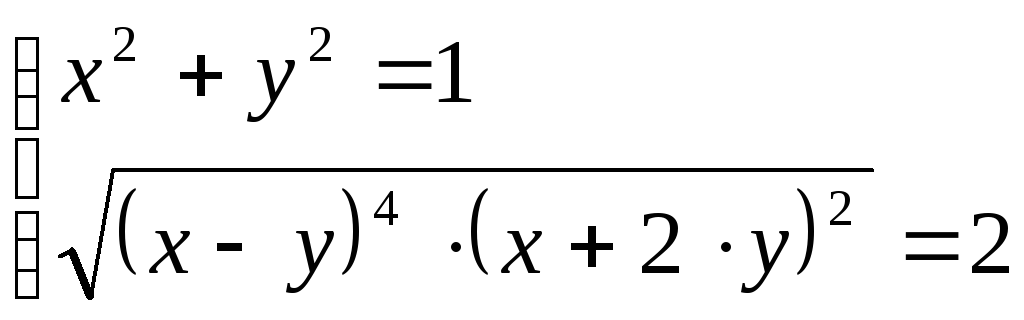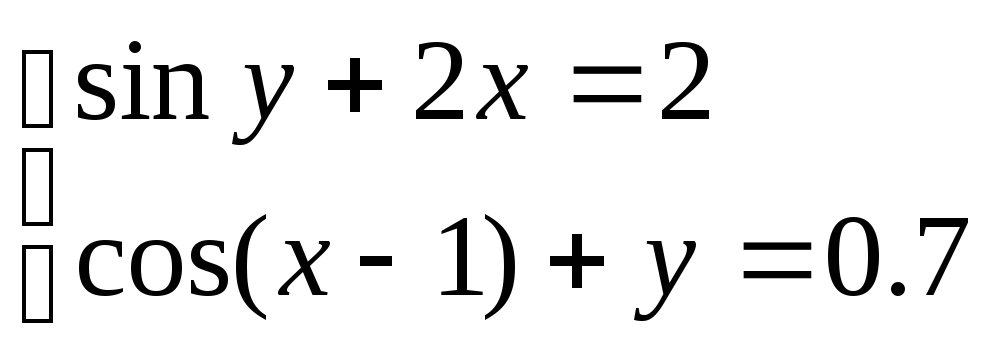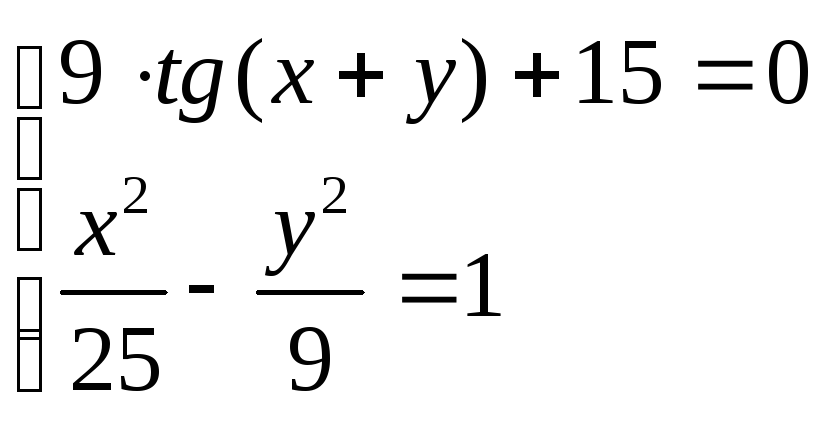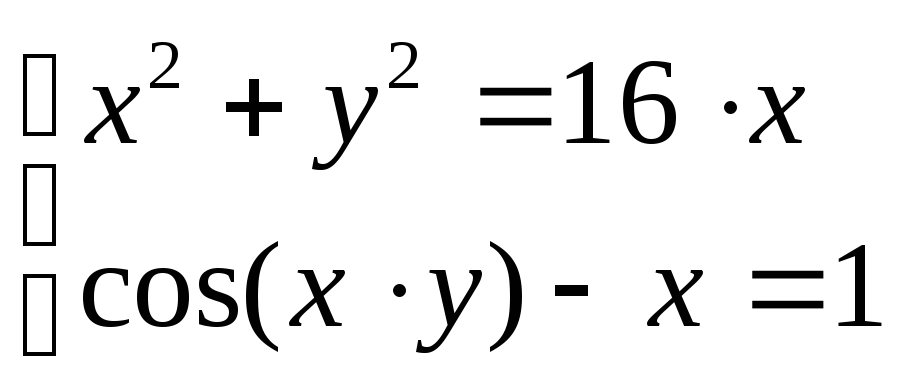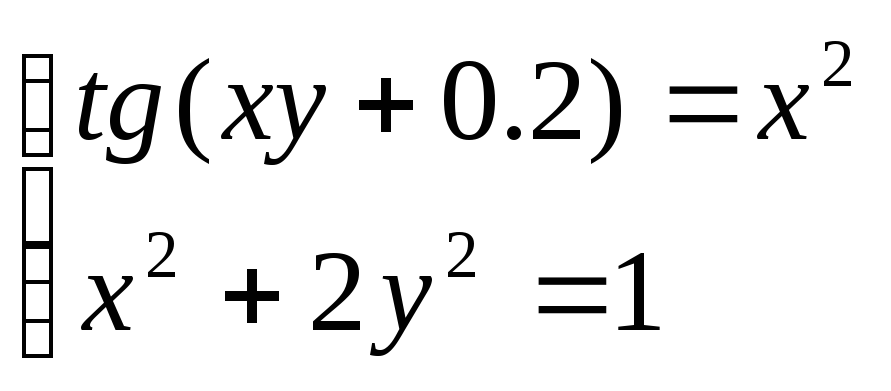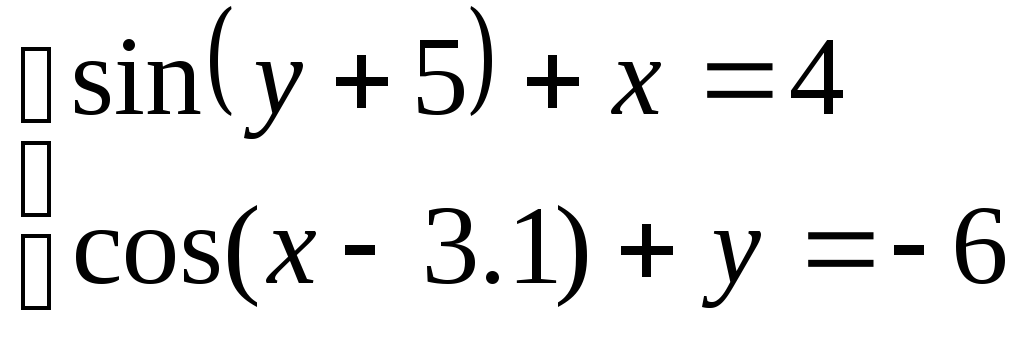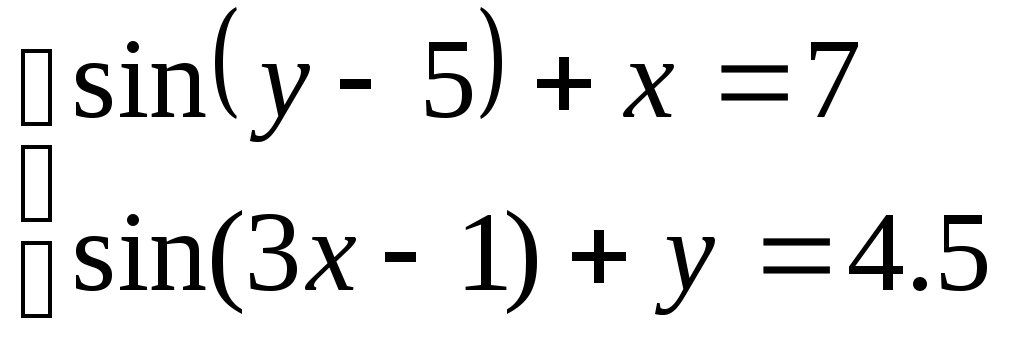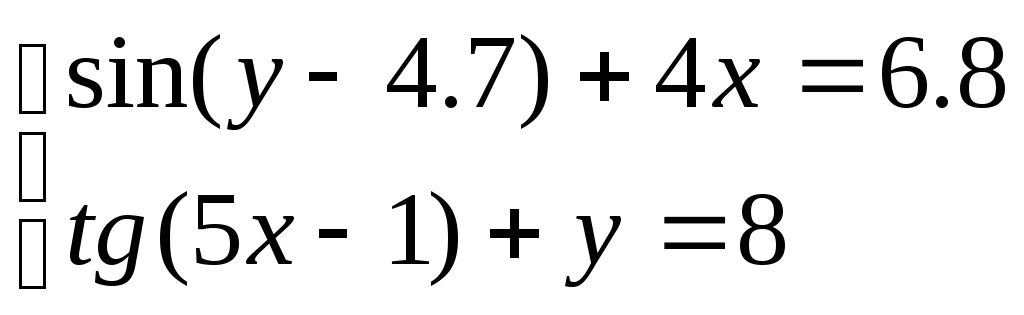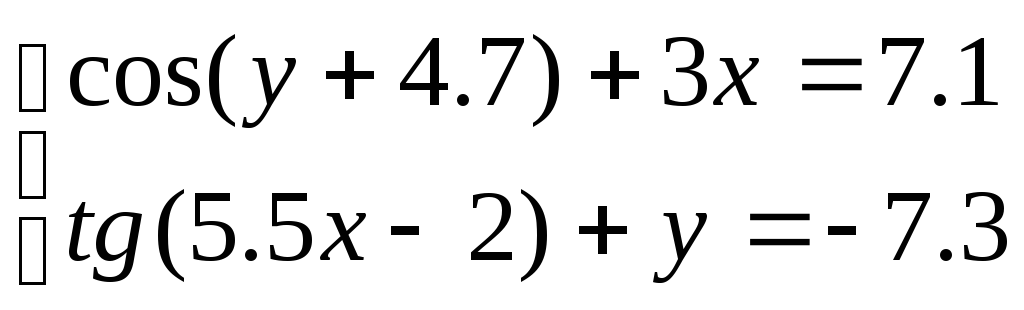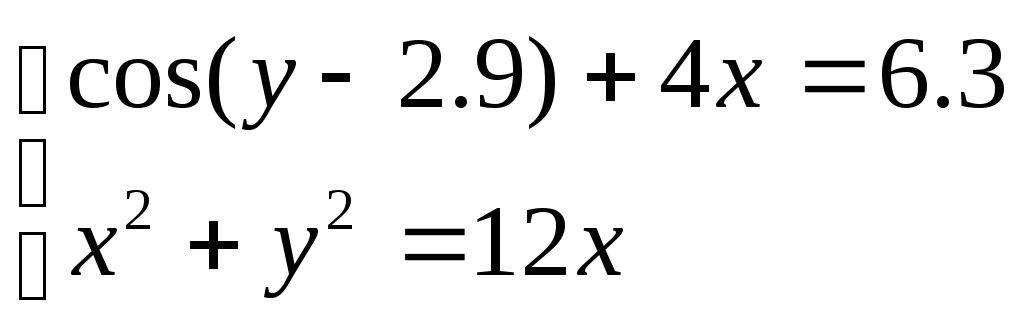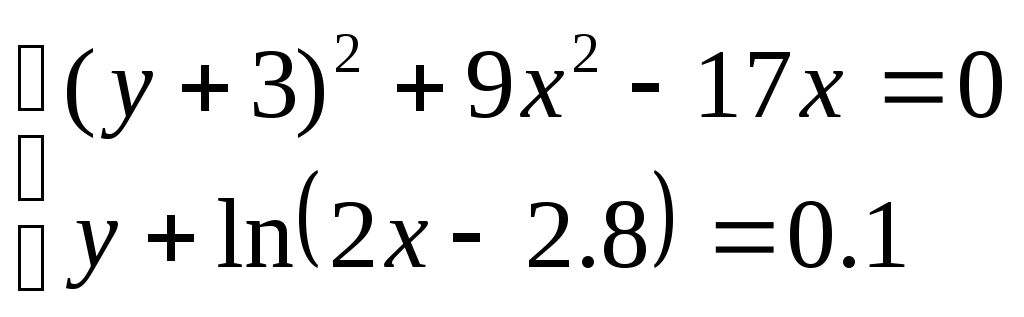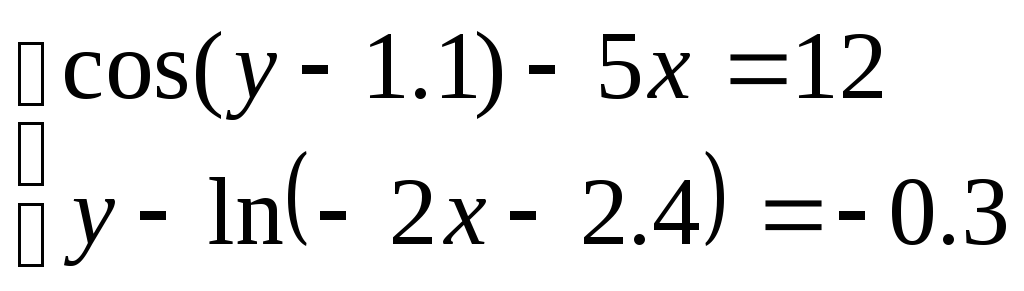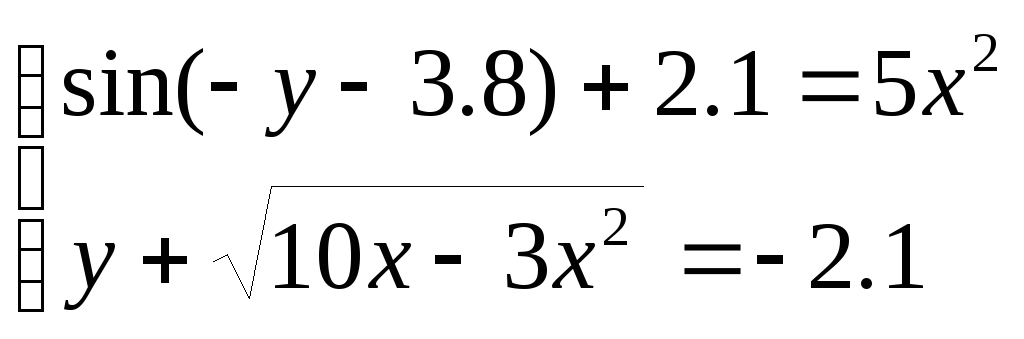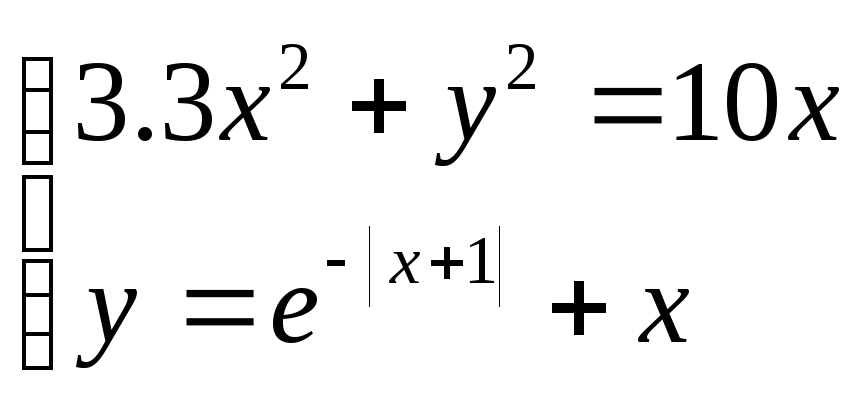2.6 Решение систем нелинейных уравнений

Цель: Освоить приемы решения систем нелинейных уравнений средствами интегрированной среды.

Задание: Решить систему уравнений .

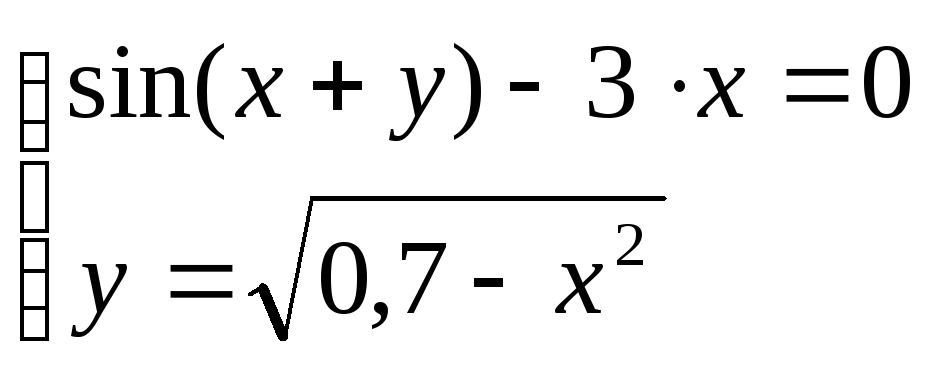Технология выполнения задания

При решении систем нелинейных уравнений можно использовать несколько способов поиска решения, отображенных на рисунке 39:

1. либо графический поиск решения системы уравнений, который состоит в построении графиков функций в одной области и определении координаты точки пересечения этих графиков методом трассировки, рассмотренном выше;

2. либо используется специальный вычислительный блок, открываемый служебным словом – директивой Given – и имеющий следующую структуру:

Начальные условия

Given

Уравнения

Ограничительные условия

Специальная функция

Начальные условия определяют начальные значения искомых переменных и задаются обычным присваиванием переменным определенных значений, то есть:

имя_переменной:=значение_переменной

Если переменных несколько, то используется векторное представление для начальных условий. Уравнения задаются в виде expr_left=expr_right с применением между левой и правой частями каждого уравнения жирного знака равенства , который находится на панели инструментов Булевый, входящей в состав панели Математическая палитра.

Ограничительные условия обычно задаются в виде неравенств или равенств, которые должны удовлетворяться при решении системы уравнений. Количество уравнений, которые можно разместить внутри вычислительного блока, ограничено и составляет 200.

В качестве специальных функций для решения системы нелинейных уравнений используют:

1. Find (v1, v2,…, vn) – возвращает значение одной или рядя переменных для точного решения;

2. Minerr (v1, v2,…, vn) – возвращает значение одной или рядя переменных для приближенного решения.

Между этими функциями существует принципиальные различия. Первая функция используется, когда решение реально существует (хотя и не является аналитическим). Вторая функция пытается найти максимальное приближение, даже к несуществующему решению, путем минимизации среднеквадратической погрешности решения.

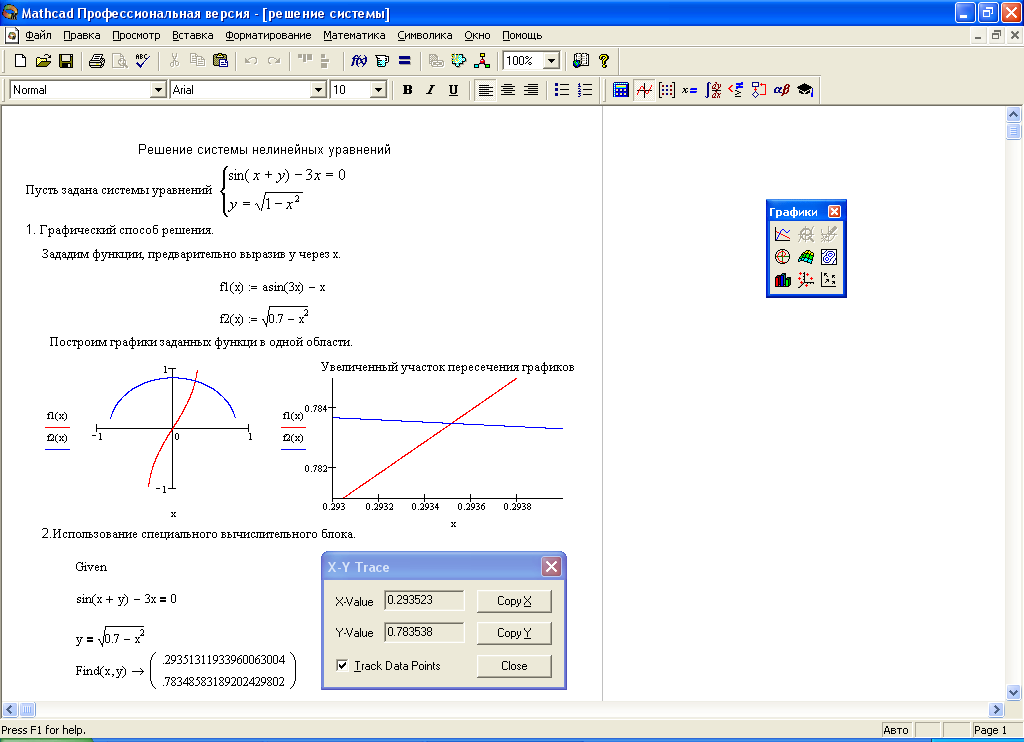
Рисунок 39 - Пример решения нелинейной системы уравнений

Таблица 18 - Индивидуальные варианты лабораторной работы №16

№ В		Варианты индивидуальных заданий
Решить систему уравнений
1			9
2			10

Продолжение таблицы 18

3		11
4		12
5		13
6		14
7		15
8		16

2.7 Решение дифференциальных уравнений

Цель: Изучить специальные функции, позволяющие осуществлять решение обыкновенных дифференциальных уравнений средствами интегрированной среды.

Задание: Найти частное решение дифференциального уравнения второго порядка , удовлетворяющего начальным условиям y(1)=0, y′(1)=3.

Технология выполнения задания

Многие серьезные физические и научно-технические задачи (особенно относящиеся к анализу динамических систем и к их математическому моделированию) базируются на решении систем дифференциальных уравнений. Нелинейные дифференциальные уравнения и системы с такими уравнениями, как правило, не имеют аналитических методов решения. Поэтому особенно важна возможность их решения численными методами и желательно представление решений в графическом виде.

Решение дифференциальных уравнений в интегрированной среде MathCAD осуществляется с помощью специальной функции odesolve(x, b[, step]).

Эта функция возвращает решение дифференциальных уравнений, описанных в блоке Given, при заданных начальных условиях и конце интервала интегрирования b. Ее можно активизировать, используя кнопку Мастера функций на панели инструментов Стандартная.

Функция имеет некоторые особенности. Например, если указано число шагов step, то решение выполняется с фиксированным шагом, иначе – адаптивным методом.

Хотя аналитическое выражение для этой функции не выводится, но графическое ее представление не вызывает затруднений, кроме того с ней можно выполнять математические преобразования.

Решение дифференциального уравнения второго порядка, указанного в задании, изображено на рисунке 40.

Дифференциальные уравнения могут быть записаны с использованием шаблонов, которые можно активизировать с помощью динамических кнопок и , расположенных на панели инструментов Калькулус или в виде , где «′» задается при помощи комбинации клавиш Ctrl + F7 .

Рассмотренная функция, для решения дифференциального уравнения, использует фиксированный шаг метода Рунге-Кутта.

Для использования адаптивного метода необходимо щелкнуть правой клавишей мыши по функции odesolve и выбрать в ниспадающем меню Adaptive.

Для решения систем обыкновенных дифференциальных уравнений в среде MathCAD они должны быть представлены в форме Коши, то есть:

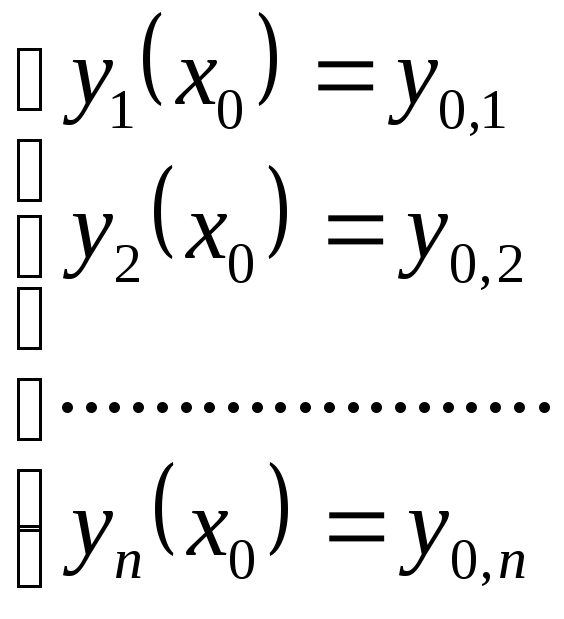- задает начальные условия, 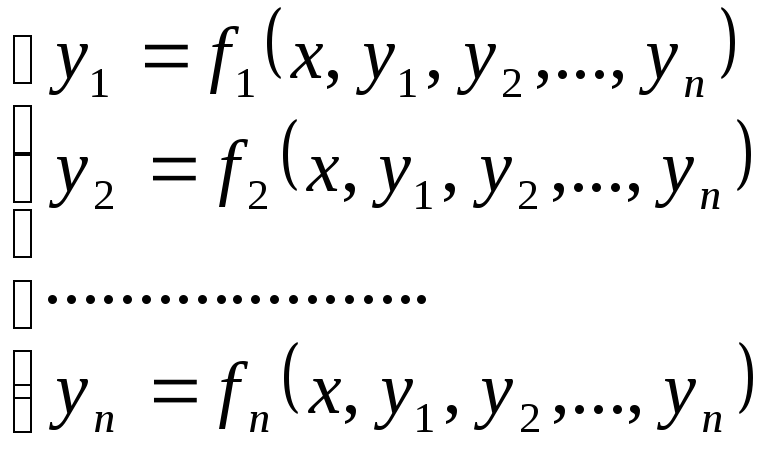- система ОДУ.

Эти системы можно представить в векторной форме: Y(x₀)=Y₀ и Y^′=F(x, Y). Тогда решение системы обыкновенных дифференциальных уравнений в форме Коши осуществляется аналогично решению одиночного дифференциального уравнения, но должно быть организовано в векторной форме. При этом добавление каждый раз очередного уравнения увеличивает число уравнений в их векторной записи.

Интегрированная среда MathCAD 2000 PRO помогает решать задачи такого класса с помощью ряда (около десятка) встроенных функций, одна из которых функция rkfixed(y, x1, x2, n, F).

Эта функция возвращает матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F на интервале от х1 до х2 при фиксированном числе шагов n.

Однако более точный результат можно получать, используя функцию Rkadapt, так как она позволяет автоматически изменять шаг, то есть она более привлекательна для решения систем дифференциальных уравнений, имеющих относительно медленно изменяющиеся решения.

Р исунок 40 - Пример решения дифференциального уравнения

Таблица 19 - Индивидуальные варианты лабораторной работы №17

№ В		Варианты индивидуальных заданий
Найти частное решение дифференциального уравнения второго порядка, удовлетворяющего указанным начальным условиям
1
2
3
4
5
6
7
8

Продолжение таблицы 19

9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

Продолжение таблицы 19

28
29
30