
- •Часть 2. «Решение уравнений и систем уравнений»
- •Харьков, 2010
- •Самостоятельные работы. Самостоятельная работа №2. Решение систем линейных уравнений. Примеры выполнения практических заданий.
- •Контрольные вопросы и задания.
- •Индивидуальные задания.
- •Самостоятельная работа №3. Решение нелинейных уравнений. Уточнение корней методом половинного деления (дихотомии)
- •Метод Ньютона для решения систем нелинейных алгебраических уравнений.
- •Индивидуальные задания.
- •Лабораторные работы. Лабораторная работа №5. Реализация методов решения уравнений и их систем средствами vba.
- •Прямой ход метода Гаусса
- •Лабораторная работа №6. Решение уравнений средствами Excel. Подбор параметра
- •Поиск решения
- •С помощью средства Подбор параметра ;
-
Прямой ход метода Гаусса
Матрица коэффициентов А вектор В
|
2 |
3 |
7 |
6 |
1 |
|
3 |
5 |
3 |
1 |
3 |
|
5 |
3 |
1 |
3 |
4 |
|
3 |
3 |
1 |
6 |
5 |
|
2 |
3 |
7 |
6 |
1 |
|
=A4:E4- $A$3:$E$3* (A4/$A$3) |
=A4:E4- $A$3:$E$3* (A4/$A$3) |
=A4:E4- $A$3:$E$3* (A4/$A$3) |
=A4:E4- $A$3:$E$3* (A4/$A$3) |
=A4:E4- $A$3:$E$3* (A4/$A$3) |
|
=A5:E5- $A$3:$E$3* (A5/$A$3) |
=A5:E5- $A$3:$E$3* (A5/$A$3) |
=A5:E5- $A$3:$E$3* (A5/$A$3) |
=A5:E5- $A$3:$E$3* (A5/$A$3) |
=A5:E5- $A$3:$E$3* (A5/$A$3) |
|
=A6:E6- $A$3:$E$3* (A6/$A$3) |
=A6:E6- $A$3:$E$3* (A6/$A$3) |
=A6:E6- $A$3:$E$3* (A6/$A$3) |
=A6:E6- $A$3:$E$3* (A6/$A$3) |
=A6:E6- $A$3:$E$3* (A6/$A$3) |
Рис. 4. Формулы первого шага прямого хода исключения
Задание 3. Построить блок-схему алгоритма и разработать VBA-программу решения системы линейных уравнений методом Гаусса.
Задание 4. С помощью созданного рабочего листа Excel и разработанной VBA-программы решить системы уравнений методом Гаусса и вычислить выражения (согласно своему варианту):
-
Решить системы линейных уравнений АХ=В, А
 Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y A
A A
A Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, А
 Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y A
A A
A Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, А
 Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y A
A A
A Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, А
 А
А Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А Y,
где
Y,
где
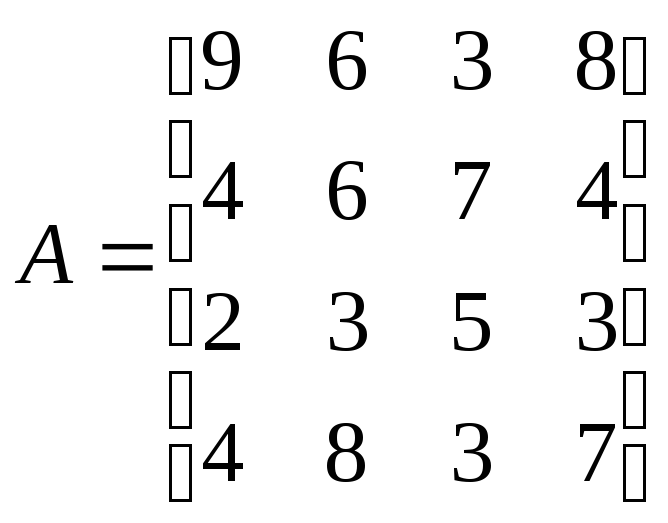 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, А
 А
А Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А Y,
где
Y,
где
![]()
 ,
,
![]()
![]() ,
,
![]()
![]()
-
Решить системы линейных уравнений АХ=В, А
 А
А Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А Y,
где
Y,
где
 ,
,
 ,
,
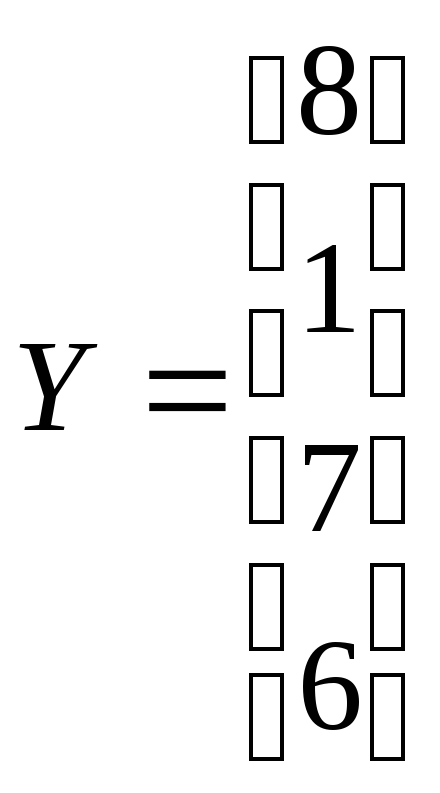
-
Решить системы линейных уравнений АХ=В, АА
 АХ=В
и вычислить значения квадратичной
формы z=Y
АХ=В
и вычислить значения квадратичной
формы z=Y А
А А
А Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА
 АХ=В
и вычислить значения квадратичной
формы z=Y
АХ=В
и вычислить значения квадратичной
формы z=Y А
А А
А Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА
 АХ=В
и вычислить значения квадратичной
формы z=Y
АХ=В
и вычислить значения квадратичной
формы z=Y А
А А
А Y,
где
Y,
где
 ,
,
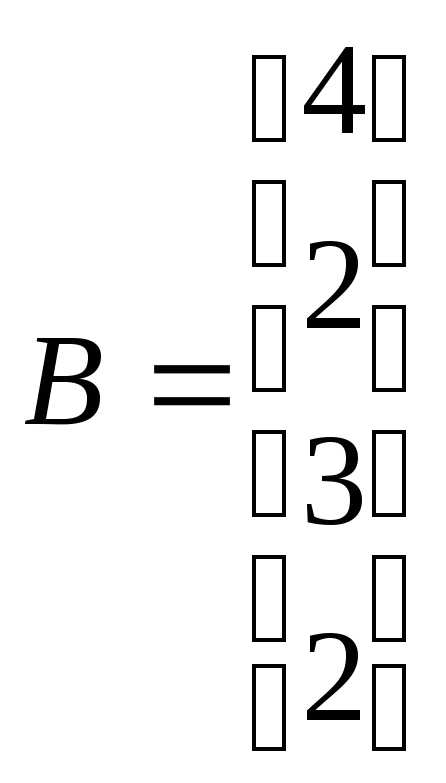 ,
,

-
Решить системы линейных уравнений АХ=В, А
 А
А АХ=В
и вычислить значения квадратичной
формы z=Y
АХ=В
и вычислить значения квадратичной
формы z=Y А
А А А
А А Y,
где
Y,
где
 ,
,
 ,
,
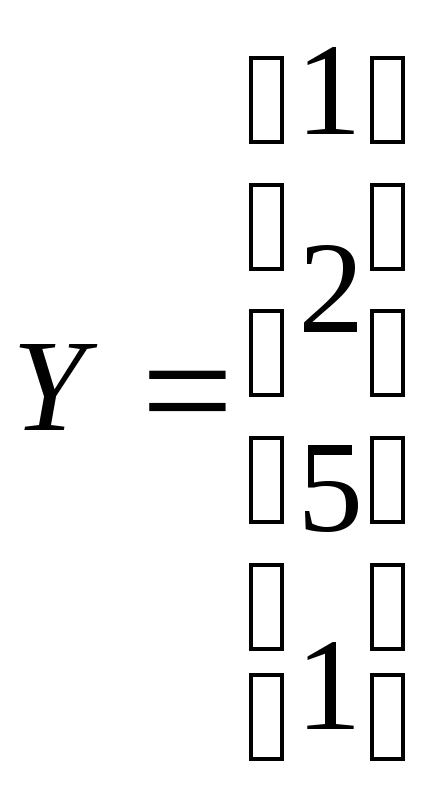
-
Решить системы линейных уравнений АХ=В, А
 А
А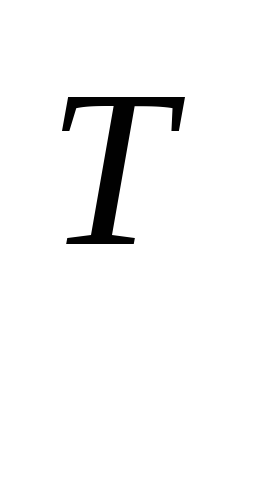 АХ=В
и вычислить значения квадратичной
формы z=Y
АХ=В
и вычислить значения квадратичной
формы z=Y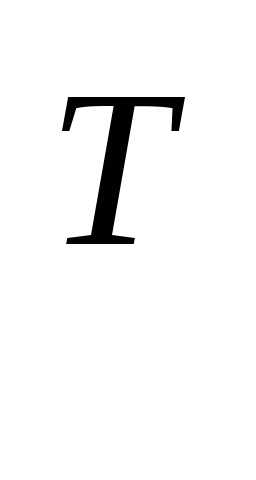 А
А А А
А А Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, А
 А
А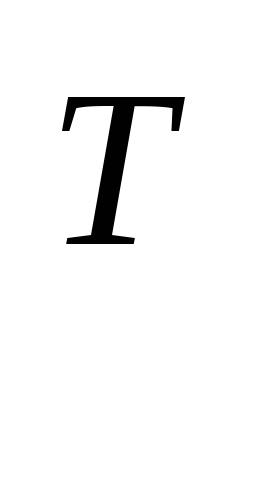 АХ=В
и вычислить значения квадратичной
формы z=Y
АХ=В
и вычислить значения квадратичной
формы z=Y А
А А А
А А Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА
 А
А Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А А
А Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА
 А
А Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А А
А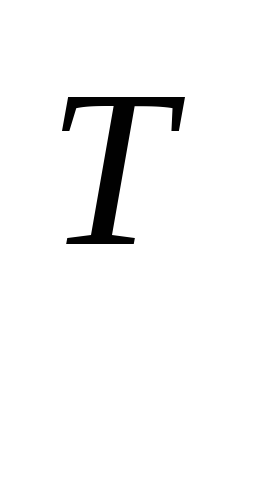 Y,
где
Y,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА
 А
А Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А А
А Y,
где
Y,
где
 ,
,
 ,
,

16. Решить
системы линейных уравнений АХ=В, А![]() А
А![]() Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y![]() А
А![]() А
А![]() АY,
где
АY,
где
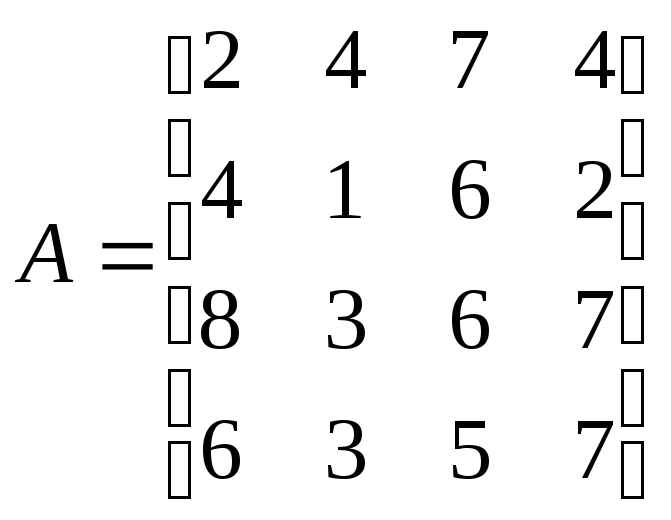 ,
,
 ,
,

17. Решить
системы линейных уравнений АХ=В, А![]() А
А![]() Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y![]() А
А![]() А
А![]() АY,
где
АY,
где
 ,
,
 ,
,

18. Решить
системы линейных уравнений АХ=В, А![]() А
А![]() Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y![]() А
А![]() А
А![]() АY,
где
АY,
где
 ,
,
 ,
,

19. Решить
системы линейных уравнений АХ=В, А![]() А
А![]() Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y![]() А
А
А
А![]() А
А![]() Y,
где
Y,
где
 ,
,
 ,
,

20. Решить
системы линейных уравнений АХ=В, А![]() А
А![]() Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y![]() А
А
А
А![]() А
А![]() Y,
где
Y,
где
 ,
,
 ,
,

21. Решить
системы линейных уравнений АХ=В, А![]() А
А![]() Х=В и вычислить значения квадратичной
формы z=Y
Х=В и вычислить значения квадратичной
формы z=Y![]() А
А
А
А![]() А
А![]() Y,
где
Y,
где
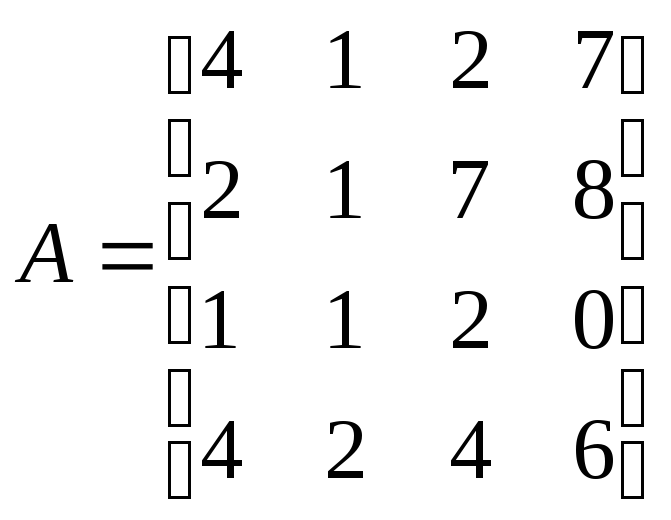 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА А
 Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А А
А АY,
где
АY,
где
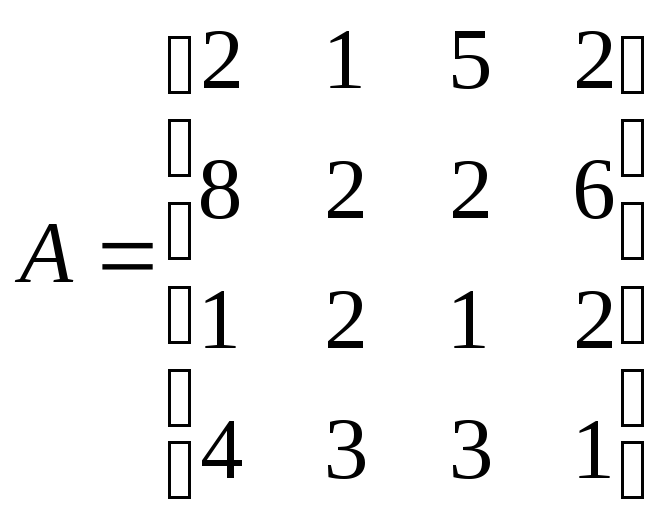 ,
,
 ,
,
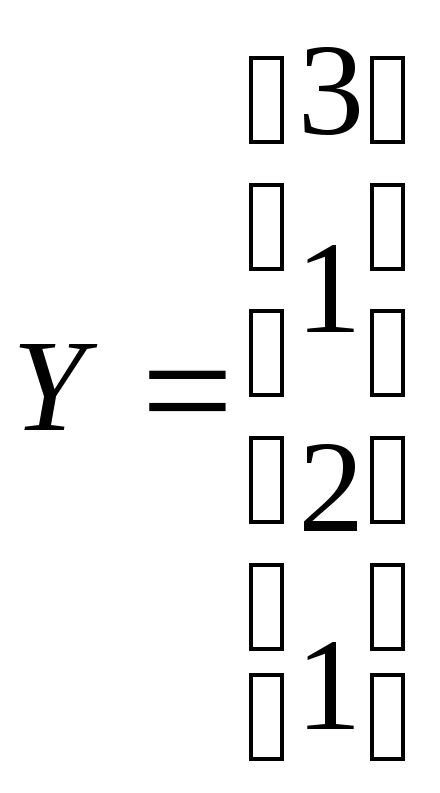
-
Решить системы линейных уравнений АХ=В, АА А
 Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А А
А АY,
где
АY,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АА А
 Х=В
и вычислить значения квадратичной
формы z=Y
Х=В
и вычислить значения квадратичной
формы z=Y А
А А
А АY,
где
АY,
где
 ,
,
 ,
,

-
Решить системы линейных уравнений АХ=В, АТААТХ=В и вычислить значение квадратичной формы z=YTAATAATY , где

26. Решить системы линейных уравнений АХ=В, АТААТХ=В и
вычислить значение квадратичной формы z=YTAATAATY , где

27. Решить системы линейных уравнений АХ=В, АТААТХ=В и
вычислить значение квадратичной формы z=YTAATAATY , где

28. Решить системы линейных уравнений АХ=В, АТААТХ=В и
вычислить значение квадратичной формы z=YTAATAATY , где

29. Решить системы линейных уравнений АХ=В, АТААТХ=В и
вычислить значение квадратичной формы z=YTAATAATY , где

30. Решить системы линейных уравнений АХ=В, АТААТХ=В и
вычислить значение квадратичной формы z=YTAATAATY , где

Задание 5. Построить блок-схему алгоритма и разработать VBA-программу поиска корня нелинейного уравнения f1(x)=f2(x) на заданном отрезке [a,b] c заданной точностью ε, реализовав в виде процедуры метод половинного деления. Используя процедуру решить уравнение приведенное таблице 1.
Задание 6. Подготовить рабочий лист в Excel для решения системы нелинейных уравнений методом Ньютона по следующему образцу (рис 4а) и решить уравнение в соответствии со своим вариантом. Значение погрешности принять равным 0,001 для всех вариантов.
|
|
Решение системы уравнений методом Ньютона |
|
||||||
|
Исходная система уравнений |
|
Производные |
|
|
|
|||
|
f1=6x1^2+x2^2+10x1=0 |
|
df1dx1=12x1+10 |
df1dx2=2x2 |
|
||||
|
f2=2x1x2+2x2=0 |
|
|
df2dx1=2x2 |
df2dx2=2x1+2 |
|
|||
|
Шаг |
|
x |
f |
W-якобиан |
W-1-обратный |
dx |
||
|
df1 |
df2 |
|||||||
|
0 |
x1 |
0,1 |
1,1 |
11,2 |
0,4 |
0,089869 |
-0,01634 |
0,091667 |
|
x2 |
0,2 |
0,44 |
0,4 |
2,2 |
-0,01634 |
0,457516 |
0,183333 |
|
|
1 |
x1 |
0,008333 |
0,084028 |
10,1 |
0,033333 |
0,099015 |
-0,00164 |
0,008265 |
|
x2 |
0,016667 |
0,033611 |
0,033333 |
2,016667 |
-0,00164 |
0,495895 |
0,01653 |
|
|
2 |
x1 |
6,83E-05 |
0,000683 |
10,00082 |
0,000273 |
0,099992 |
-1,4E-05 |
6,83E-05 |
|
x2 |
0,000137 |
0,000273 |
0,000273 |
2,000137 |
-1,4E-05 |
0,499966 |
0,000137 |
|
|
3 |
x1 |
4,67E-09 |
4,67E-08 |
10 |
1,87E-08 |
0,1 |
-9,3E-10 |
4,67E-09 |
|
x2 |
9,33E-09 |
1,87E-08 |
1,87E-08 |
2 |
-9,3E-10 |
0,5 |
9,33E-09 |
|
Рис. 4а. Рабочий лист Excel для решения системы уравнений методом Ньютона.
Задание 7. Построить блок-схему алгоритма и разработать VBA-программу решения систем нелинейных уравнений методом Ньютона. С заданной точностью ε=0,001.
Задание 8. Преобразовать нелинейные уравнения системы из Таблицы 3а к виду f 1(x) = y и f 2 (y)= x. Построить их графики и определить начальное приближение решения. Затем решить с помощью метода Ньютона.
Таблица 3а. Задания к методу Ньютона
|
№ |
Задание |
№ |
Задание |
№ |
Задание |
|
1 |
|
11 |
|
21 |
|
|
2 |
|
12 |
|
22 |
|
|
3 |
|
13 |
|
23 |
|
|
4 |
|
14 |
|
24 |
|
|
5 |
|
15 |
|
25 |
|
|
6 |
|
16 |
|
26 |
|
|
7 |
|
17 |
|
27 |
|
|
8 |
|
18 |
|
28 |
|
|
9 |
|
19 |
|
29 |
|
|
10 |
|
20 |
|
30 |
|
