Самостоятельная работа №3. Решение нелинейных уравнений. Уточнение корней методом половинного деления (дихотомии)

Самым простейшим из методов уточнения корней является метод половинного деления, или метод дихотомии, предназначенный для нахождения корней уравнений, представленных в виде f(x)=0.

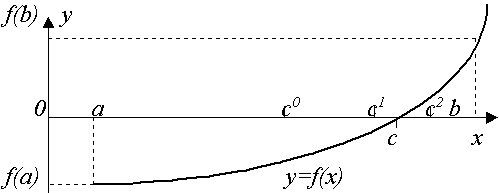
Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)f(b) 0 (рис. 1), тогда на отрезке имеется хотя бы один корень.

Рис. 1. Метод деления отрезка пополам

Возьмем середину отрезка с=(a+b)/2. Если f(a) f(c)  0, то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b.

Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (b-a)<e.

Так как каждое очередное вычисление середины отрезка c и значения функции f(c) сужает интервал поиска вдвое, то при исходном отрезке [a,b] и предельной погрешности e  количество вычислений n определяется условием (b-a)/2ⁿ<e , или n~log₂((b-a)/e ). Например, при исходном единичном интервале и точности порядка 6 знаков (e ~ 10^-6) после десятичной точки достаточно провести 20 вычислений (итераций) значений функции.

С точки зрения машинной реализации этот метод наиболее прост и используется во многих стандартных программных средствах, хотя существуют и другие более эффективные по затратам времени методы.

Метод Ньютона для решения систем нелинейных алгебраических уравнений.

Пусть известно некоторое приближение к корню . Запишем исходную систему нелинейных уравнений в виде

где . Разлагая эти уравнения в ряды и ограничиваясь первыми дифференциалами, т.е. линеаризуя функцию, получим

Это система уравнений, линейных относительно приращений ; все коэффициенты системы выражаются через последнее приближение . Решив эту систему, например, методом исключения найдем новое приближение .

Отметим, что система (6.13) в матричной форме имеет вид:

где значения производных в матрице коэффициентов и функций в векторе свободных членов вычислены при текущем приближении корня .

Матрица частных производных носит название матрицы Якоби. Для ее формирования возможны два пути: а) получить аналитические выражения для всех частных производных и вычислить их значение при – прием предпочтительный в смысле корректности подхода, но зачастую трудоемкий, особенно при большом числе аргументов; б) заменить частные производные в матрице Якоби их приближенными конечно-разностными значениями

где – малое приращение .

Алгоритм решения системы нелинейных уравнений методом Ньютона складывается из следующих этапов:

1) задают относительную погрешность вычисления аргументов , вектор начальных приближений , максимальное число итераций M для выхода из алгоритма в случае медленной сходимости или программных ошибок пользователя;

2. вычисляют матрицу Якоби по аналитическим выражениям или конечно-разностным методом, причем в последнем случае можно принять

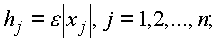
3. решают систему линейных алгебраических уравнений (6.14) относительно приращений

4) вычисляют уточненное значение аргументов – новое приближение по формуле

5) проверяют выполнение условий по всем аргументам и если хотя бы одно выполняется, то возвращаются к п.2 для новой итерации; в противном случае полученный вектор считают решением.