4. Элементы теории массового обслуживания.

Системы массового обслуживания (СМО) отождествляются с ожиданием в очереди (например, у врача) и без ожидания (телефонная сеть, если номер занят, то необходимо еще раз набрать номер). По типу поступления заявок системы могут быть открытыми и замкнутыми. Пусть интенсивность потока покупателей в магазине ~ 95 чел/час, а один продавец обслуживает ~ 20 чел/час. Сколько нужно иметь продавцов? Как минимум 5, иначе очередь будет расти. Но очередь будет и при 5, и при 6 продавцах из-за нерегулярности потока и времени обслуживания. Длина очереди и время ожидания обслуживания – случайные величины. Пусть M[*] – оператор математического ожидания. Мы хотим научиться быстро определять M[время ожидания в очереди].

Ж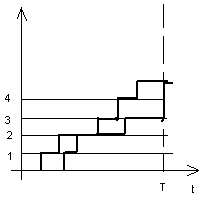изнь каждой заявки можно схематично отразить так: в момент времени она поступает в очередь, стоит до момента t, обслуживается и уходит из очереди. Пусть (t) - число поступивших к моменту t заявок, (t) - число обслу­женных заявок. Будем считать, что в любой момент времени может поступить или быть обслужена только 1 заявка и (t)  (t), т.к. не может быть обслужено заявок больше, чем поступило. Рассмотрим величины, усредненные по интервалу [0,t]:

Площадь фигуры между графиками (t) и (t) за период времени [0,t] есть - суммарное время нахождения всех заявок в системе (т.е. в очереди или на обслуживании).

T_t - среднее время нахождения одной заявки в системе за время от 0 до t;

N_t - среднее число заявок, находящихся в системе в любой момент времени.

_t - среднее число заявок, поступавших за единицу времени (интенсивность потока заявок).

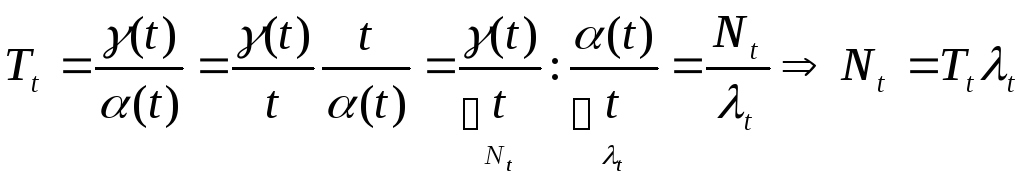
Если две из величин N_t,T_t и _t имеют предел при , то и третья имеет предел, и выполняется формула Литтла:

4.1. Пуассоновский поток событий

Событие состоит в том, что за интервал в систему поступает k заявок.

Поток событий – пуассоновский, если

1. т.е. события независимы (отсутствие последействия – вероятность поступления m заявок на интервале не зависит от того, сколько их поступило раньше).

2. - вероятность поступления заявки в интервале длины h пропорциональна длине интервала. Поток стационарный, если .

3. – вероятность того, что на очень маленьком интервале времени поступает более 1 заявки, есть o(h) (ординарность потока).

Простейший поток событий = ординарный, стационарный и без последействия.

4. 5.

Введем обозначения:

Посчитаем и :

1.

(по определению ). Последнее уравнение легко решить: т.к. , то

, причем, если t=0, то

- это вероятность того, что на интервале от 0 до 0 произойдет 0 событий, тогда с=1 (по свойству 5), т.е. .

2.

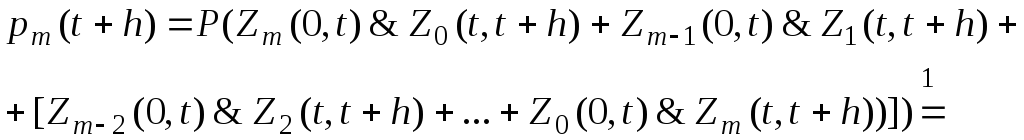
парные события несовместимы, интервалы (0,t) и (t,t+h) – не пересекаются.

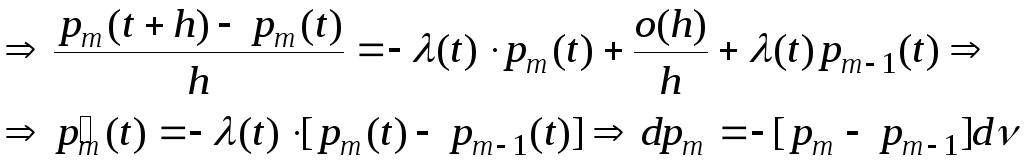
Легко проверить свойства: (для проверки: на интервале (0,h):

m=1, по свойству 2: ). Так как , то

Одно из решений: . Но других решений нет. Т.е. число заявок распределено по закону Пуассона с параметром : дискретная сл.величина распределена по закону Пуассона с параметром а, если .

Посчитаем: М[числа заявок, поступивших на интервале (0,t)] =

.

Тогда M[числа пост. заявок]=, - некоторое число.

Если - для простейшего потока.

- мат. ожидание числа заявок на (0,t+h),

- скорость (интенсивность) поступления заявок.