3.5. Потоковые задачи Задача о максимальном потоке (змп).

Пусть S – сеть, т.е. граф (V,E) с выделенными стартовой и терминальной вершинами s, t V; A ={ _ij  0} – матрица пропускных способностей ребер,  _ij = 0  ребра нет; поток X ={x _ij}– матрица, удовлетворяющая ограничениям:

0  x _ij   _ij , _j x _ij = _k x _ki ,  i  s,t – уравнение баланса.

Максимизируем величину потока, вытекающего из вершины s: F( X ) = _j x _sj .

Предположение А. r= min{x_ij, x_ji} = 0. Иначе проводим операцию ГАШЕНИЕ: x_ij= x_ij– r, x_ji = x_ji– r. Поток при этом остается допустимым. В том числе x_ii = 0. Предположение Б. x _js = x _tj = 0 (в s ничего не втекает, из t ничего не вытекает).

На диагонали матрицы X стоят нули. Суммы элементов первой строки и последнего столбца равны. Для остальных строк: сумма элементов строки i равна сумме элементов i-го столбца.

Все ограничения и целевая функция линейны  это задача ЛП.

Как и задача о кратчайшем пути, она может решаться волновым алгоритмом.

Пусть W – множество включенных вершин: WV, sW, tW. Обозначим через R(W) ={(v₁,v₂)E | v₁W, v₂W}  -разрез,R(W) ={(v₁,v₂)E | v₁W, v₂W} -антиразрез,  (R (W )) =  - пропускную способность разреза.

Теорема 1: Для любого потока X и для любого W .

Доказательство. Имеем .

Следствие 1. _j x _sj = _k x _kt . Для этого достаточно взять W = V \ {t}.

Следствие 2. Для любого потока X и для любого W имеем F (X) ≤  (R (W )) .

Доказательство: .

Неравенство верно для любых X и W  .

Теорема 2 (Форда-Фалкерсона):

Доказательство. Пусть по сети течет поток X. Поток из i в j можно увеличить на величину _ij = x_ji +(α_ij - x_ij), погасив поток по обратной дуге (j,i) и послав дополнительный поток по прямой дуге (i,j). Ориен­тированную дугу назовем аугментальной (допускающей увеличение потока), если _ij > 0. По крайней мере одна из дуг (i,j) и (j,i) будет аугментальной при любом потоке X. Построим ориентированную A‑сеть из аугментальных дуг и найдем в ней аугментальную цепь L дуг из s в t, решив задачу на достижимость. Сначала включим вершину S. Из включенной вершины i можно включить любую соседнюю вершину j. Алгоритм Форда-Фалкерсона (АФФ) включает вершины в произвольном порядке до тех пор, пока что-либо можно включить. Процесс заканчивается, когда включена вершина t. Обратным ходом находим цепь L из s в t. Пошлем по ней дополнительный поток величины  =. Суммарный поток – допус­тимый, т.к. 0  x _ij   _ij  и выполнены уравнения ба­ланса. Затем все включения отменяем и повторяем все сначала. Алгоритм оста­навливается, когда для разреза R(W) все _ij = 0, т.е. все обратные дуги нулевые, а все прямые - насыщены  пропускные способности дуг равны потокам.  По теореме 1 имеем F (X) =  (R (W ))   . ■

Замечание. Если _ij для всех дуг – целые числа, то  - целое и на каждой итерации поток увеличивается как минимум на 1  через конечное число шагов алгоритм остановится. Но он может не остановиться, если _ij иррациональны.

Пример 1. При плохом выборе аугментальных цепочек АФФ может сделать 2000 итераций, т.е. трудоемкость зависит от ПС, а не от числа вершин. Эдмондсон и Карп насыщали аугментальные цепи с минимальным числом ребер.

№23. А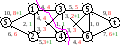 лгоритм Диница – Карзанова (АДК).

Описание алгоритма дадим на примере 2. На ребрах сети S до запятой стоят пропускные способности, после запятой – сумма потоков на этапах.

а) Основной цикл идет по этапам:

строим слоистую сеть всех кратчайших путей и насыщаем ее за O(n²) операций. Максимальный поток строится за n этапов с общей трудоемкостью O(n³).

Э тап №1: Для текущего потока x строим слоистую сеть S(x). Поиск «сначала вширь», структура – очередь вершин s / 1, 2 / 3, 4 / 5, 6 / t, разбитых на слои. На слой 1 помещаем вершину s, на следующий слой - вершины, достижимые из вершин предыдущего слоя с помощью одного ребра, пропускная способность которого _ij = (_ij - x_ij) + x_ji  0.

Только ориентированные ребра, идущие с предыдущего слоя на следующий, у которых _ij  0, включаются в сеть S(x).

Шаг1. k=2, ƒ=F=6. Для всех вершин i ≠ s, t найдем характеристики:

• входная пропускная способность (вхПСВ(i) =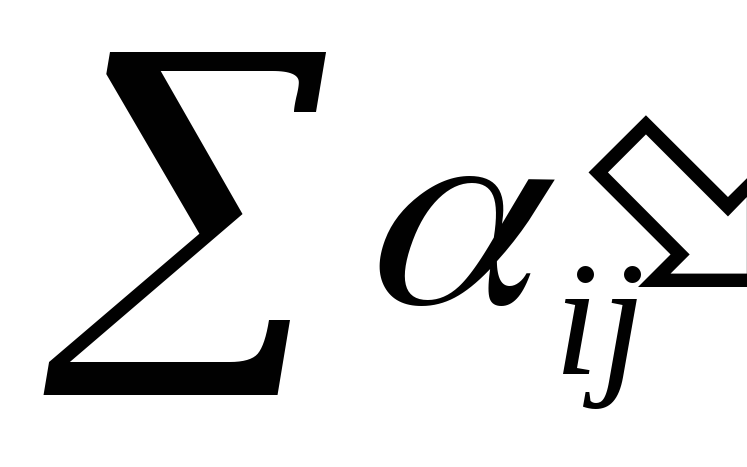по входящим дугам);

• выходная пропускная способность (выхПСВ(i) =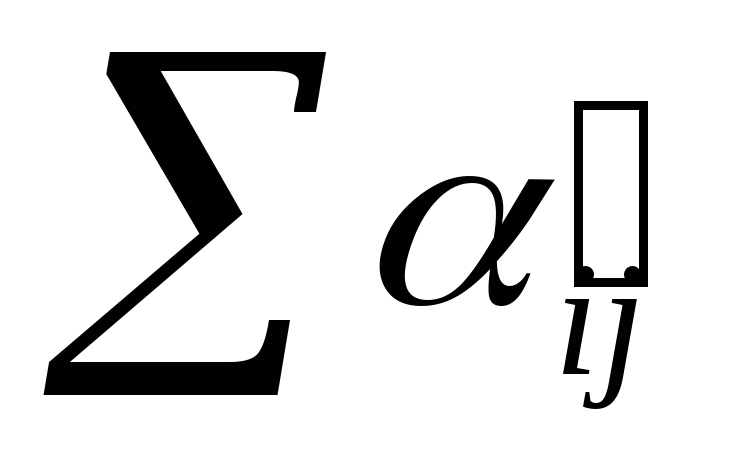по исходящим дугам)

ОЧИСТКА: Если ƒ = 0, то вершина k – зависшая, пускать нечего и можно сразу удалить вершину k.  На последнем слое останется только одна вершина - t.

Принцип ТЯНИ-ТОЛКАЯ: если из вершины k = argmin ПСВ(i) толкать в разные сторо­ны поток ƒ = ПСВ(k) со слоя на слой, то все придет слева в s (на слое 0 одна вершина s), а справа – в t (после ОЧИСТКИ там осталась одна вершина t).

Принцип НАКОПЛЕНИЯ: за счет послойной обработки дуг в процессе про­тягивания-проталкивания потока все входящие в вершину потоки сначала суммируются, а затем выталкиваются из вершины 1 раз.

b ) Цикл внутри этапа по шагам: проталкиваем из вершины k = argmin ПСВ(i) поток ƒ = ПСВ(k) в разные стороны со слоя на слой, пока слева поток не дойдет до s, а справа - до t. Проталкивание из k в s называют протягиванием из s в k. На пройденных ребрах величину потока вычитаем из вх и выхПСВ. После протягивания удаляем вершину k и проводим очистку сети S(x): удаляем провисшие ребра, суммарный поток по ним переносим в основную сеть, а их остаточные ПС вычитаем из соответствующих ПСВ слоистой сети.

Э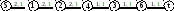 тап 2: f=1, F=15

Слоистая сеть является цепью  min ПСВ =  алгоритма Форда-Фалкерсона, вычислять ПСВ не надо. У нас цепь,  = 1  сразу переносим поток в сеть S.

Этап 3: W = {s,1,2,4}. Больше включить ничего нельзя. Величина текущего потока равна сумме пропускных способностей ребер разреза R(W): 15 = 4+3+1+3+4  поток – максимален, а разрез – минимален.

Отличия АФФ от АДК. 1) АФФ недетерминирован и АДК уточняет его.

2) Итерации АДК разделены на 2 типа: этапы и шаги. 3) АДК насыщает не цепь, а слоистую сеть  на следующей итерации отключено не ребро (одно из n·n), а вершина (одна из n на весь этап). 4) Умное проталкивание потока со слоя на слой с однократным за шаг выталкиванием потока из любой вершины.

Трудоемкость: Докажем сначала, что любой этап имеет трудоемкость N ².

1. построение слоистой сети и вычисление пропускных способностей всех ребер и вершин (ПСВ) ~ числу ребер ~ O(N²)

2. на каждом шаге основного цикла:

1). Находим вершину с min ПСВ ~ N

2). Протянуть и протолкнуть ~ О(числа ребер) ~ O(N²)

3). Удаляем вершину ~ O(N) вместе с очисткой. Результаты шага переносим в основной граф при удалении ребра из слоистой сети.

При пропускании любого потока по любой дуге слоистой сети мы вешаем на ней один флаг: если дугу насытили, то – красный, иначе – зеленый. На каждом шаге мы тянем-толкаем поток из вершины k волновым алгоритмом, т.е. со слоя на слой. При этом прийти в промежуточную вершину можно по многим дугам с разными флагами на них, а при выходе мы вешаем красные флаги до тех пор, пока нам не удастся вытолкнуть весь остаток потока, и тогда вешаем зеленый флаг. Т.к. на шаге поток из любой вершины выталкивается 1 раз, а число шагов на этапе  N (на каждом шаге удаляется вершина),  число зеленых флагов за этап = NN = N². Число красных флагов за этап  числа дуг (по красной дуге поток не пускаем). Трудоемкость этапа определяется общим числом красных и зеленых флагов ~ O(N²), а число этапов < N (т.к. номер слоя, содержащий вершину t, строго возрастает от этапа к этапу).  Общая трудоемкость алгоритма = O(N³).

Иллюстрацию работы алгоритма дает в примере 2 шаг 1 этапа 1: при выталкивании потока величины 6 из вершины 2 мы вешаем один красный флаг на ребре (2,3) и один зеленый на ребре (2,4). При обработке вершины 5 на этом же шаге поток суммируется по всем входящим в нее ребрам и выталкивается из вершины 5 с одним!!! зеленым флагом.

П ример 3. Этап 1: ОЧИСТКА. Осталась цепочка.

Зависшие вершины – удаляем сразу. = F=1.

Э тап 2:

₆₅ = x₅₆ +(α₆₅ - x₆₅) =1+1=2

= 2, F=3.

Э тап 3:

F_max = 3. Мин. разрез показан волнистой линией.

№24. Минимальный разрез в графе за O(n·|E|): алгоритм Поддерюгина.

Найти минимальный разрез в графе можно с трудоемкостью O(n⁵), выполнив алгоритм Диница-Карзанова для всех пар вершин S и T. Алгоритм Поддерюгина решает эту же задачу за O(n | E |): на i-том этапе ищется по шагам максимальный поток в вершину с номером i+1 из объединения U всех вершин с номерами j  i.

Шаг А) Пускаем поток по всем прямым ребрам из U в вершину с номером i+1.

Шаг Б) Пускаем поток по всем путям длины 2 из U в вершину с номером i+1. Для этого строим пересечение списков L_U и L_i+1 (соседи объединения и соседи вершины i+1).

Шаг В) Пускаем поток по всем путям длины  3 из U в вершину с номером i+1, удалив сначала насыщенные ребра. Строим слоистую сеть, используя обычный поиск сначала вширь (как в алгоритмах Прима и Дейкстры).

Пример.

Этап 1. А) Есть 1 прямой путь из U= {1} в 2. f_А= 1.

Б) L_U= {2,3,4}; L₂= {1,3,5}; L_U  L₂= {3}; f_Б= 1.

В) W={1 | 4 | 3,8 | 6,7 | 5 | 2}; f_В= 1.

W₁={1}. F₁= 3.

Этап 2. А) Есть 2 прямых пути из U= {1,2} в 3. f_А= 2.

Б) L_U= {3,4,5}; L₃= {1,2,4}; L_U  L₃= {4}; f_Б= 1.

В) W₂={1,2 | 5 | 6,7 | 8 | 4}; f_В= 0. F₂= 3.

Этап 3. А) Есть 2 прямых пути из U= {1,2,3} в 4. f_А= 2.

Б) L_U= {4,5}; L₄= {1,3,8}; L_U  L₄= {}; f_Б= 0.

В) W={1,2,3 | 5 | 6,7 | 8 | 4}; f_В= 1.

W₃={1,2,3}. F₃= 3.

Этап 4. А) Есть прямой путь из U= {1,2,3,4} в 5. f_А= 1.

Б) L_U= {5,8}; L₅= {2,6,7}; L_U  L₅= {}; f_Б= 0.

В) W={1,2,3,4 | 8 | 6,7 | 5}; f_В= 1.

W₄={1,2,3,4}. F₄= 2.

Этап 5. А) Есть прямой путь из U={1,2,…,5} в 6. f_А= 1.

Б) L_U= {6,7,8}; L₆= {5,7,8}; L_U  L₆= {7,8}; f_Б= 2.

В) W₅={1,2,3,4,5}; f_В= 0. F₅= 3.

Этап 6. А) Есть 2 прямых пути из U={1,…,6} в 7. f_А= 2.

Б) L_U= {7,8}; L₇= {5,6,8}; L_U  L₇= {8}; f_Б= 1.

В) W₆={1,2,3,4,5,6 | 8}; f_В= 0. F₆= 3.

Этап 7. А) Есть 3 прямых пути из U={1,…,7} в 8. f_А= 3.

Б) L_U= {8}; L₈= {4,6,7}; L_U  L₈= {}; f_Б= 0.

В) W₇={1,2,3,4,5,6,7}; f_В= 0. F₇= 3.

Минимальный разрез (F_min = 2) определяется на шаге 4 = argmin F_i множеством включенных вершин W=W₄={{1,2,3,4}}. Трудоемкость алгоритма: можно упорядочить списки соседей и найти их пересечение за линейное время; число итераций шага B за все этапы ≤ n, т.к. никакая вершина не может быть пред­последней в жирных цепочках более одного раза. На этом же этапе нельзя из-за ПСР=1, а уже на следующем этапе вершина попадет на слой 1 (т.к. соседняя с ней последняя вершина жирной цепочки включается в U). Но на шаге В номер предпоследнего слоя  2!!! Шаги А и Б оцениваются легко.

Обоснование корректности алгоритма: пусть R(W) - минимальный разрез графа, 1W и k=minW ≥2  R(W) будет найден на шаге k.

№25. Задача о потоке минимальной стоимости (ПМС).