Контрольная работа

Статистический анализ точности операций механической обработки

Цель работы – ознакомление со статистическими методами оценки случайных погрешностей механической обработки; приобретение навыков обработки результатов измерения партии деталей; определение показателей точности технологической операции по исследуемому параметру.

Общие сведения

Под точностью в технологии машиностроения понимается степень адекватности производимых изделий их заранее установленному эталону. Точность детали определяется соответствием её требованиям чертежа по размерам, геометрической форме, правильности взаимного расположения обрабатываемых поверхностей и их шероховатости. Существующие методы достижения точности сопровождаются различного рода погрешностями, возникающими при изготовлении заготовок, обработке резанием, контроле, сборке и других видах обработки.

Погрешность обработки рассматривается как мера точности и представляет собой отклонение полученного значения параметра от заданного (требуемого).

Погрешности, возникающие в процессе обработки на металлорежущих станках, могут носить систематический или случайный характер. Систематические погрешности, в свою очередь, можно разделить на постоянные и закономерно изменяющиеся (называемые функциональными).

Причинами появления систематических постоянных погрешностей могут быть такие: погрешности изготовления и компоновки станка, погрешности режущего инструмента, приспособлений, системы автоматизированного управления обработкой (например, управляющей программы с ЧПУ) и др. Постоянные погрешности не изменяются при обработке партии заготовок, выявляются пробными измерениями. Соответствующими технологическими мероприятиями или приёмами они могут быть сведены к минимуму.

Функциональные погрешности влияют на точность обработки непрерывно или периодически по определённым законам. Причинами таких погрешностей являются: размерный износ режущего инструмента, эксплуатационный износ станка, жёсткость технологической системы СПИД (станок – приспособление – инструмент – деталь), температурные явления в зоне резания, условия трения, колебаний и др.

Случайные погрешности вызываются влиянием на процесс обработки ряда независимых друг от друга случайных факторов. Такие погрешности в партии заготовок имеют разные значения, причём их появление не подчиняется видимой закономерности. Случайными факторами могут быть: неточность установки заготовки в приспособлении, колебания системы СПИД, вызванные нестабильностью сил резания (из-за колебаний твёрдости материала, припусков и т.п.), остаточные напряжения после предшествующей обработки, отклонения параметров управляющей программы для станков с ЧПУ и др.

Влияние случайных факторов выражается в рассеянии размеров конкретного параметра исследуемой партии заготовок, обрабатываемых при одних и тех же условиях. Таким образом, истинные (действительные) размеры каждой заготовки обрабатываемой партии являются случайными величинами и могут принимать любые значения в границах определённого интервала.

Совокупность значений истинных размеров заготовок n, обработанных при неизменных условиях и расположенных в возрастающем порядке с указанием частоты m_i повторения этих размеров, называют распределением размеров заготовок. Измеренные значения истинных размеров заготовок разбивают на интервалы и разряды N. Частость – это отношение количества заготовок, действительные размеры которых попали в данный интервал m_i, к общему количеству заготовок партии: .

При разных условиях обработки заготовок рассеяние (распределение) их истинных размеров подчиняется различным математическим законам: нормального распределения (закон Гаусса), равнобедренного треугольника (закон Симпсона), равной вероятности, закону эксцентриситета (закон Релея) и др.

Наиболее часто распределение действительных размеров заготовок, обработанных на настроенных станках, подчиняется закону нормального распределения, уравнение кривой которого имеет вид:

y = 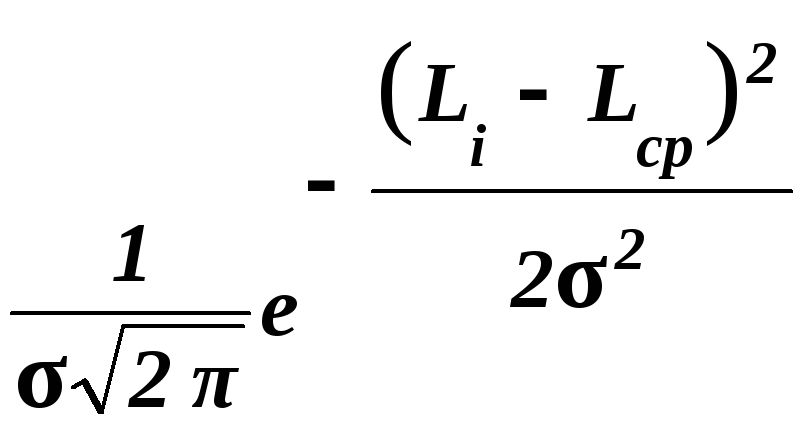, (1)

где – среднее квадратическое отклонение.

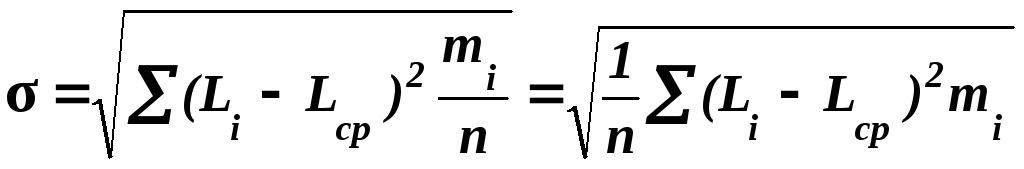, (2)

где L_i – текущий размер;

L_ср – среднее арифметическое значение действительных размеров заготовок данной партии.

L_ср = , (3)

здесь m_i – частота (количество заготовок данного интервала размеров);

n – количество заготовок в партии.

А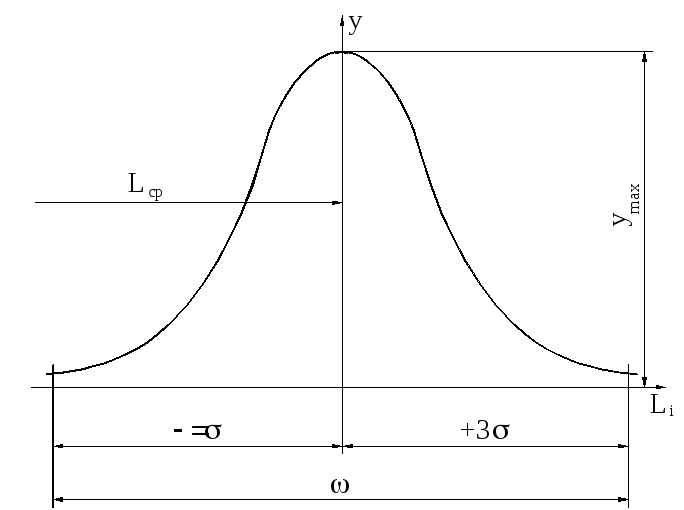 нализ уравнения (1) показывает, что кривая нормального распределения (рис. 13) симметрична относительно оси ординат и асимптотически приближается к оси абсцисс.

Рис. 13. Кривая нормального распределения (закон Гаусса)

При L_i = L_ср кривая нормального распределения имеет максимум y_max = .

На расстоянии от положения вершины кривой её ветви так близко подходят к оси абсцисс, что в этих пределах оказывается 99,73 % площади, заключённой между всей кривой и осью абсцисс. На практике обычно принимают, что на расстоянии от положения вершины кривой нормального распределения её ветви пересекаются с осью абсцисс, ограничивая 100 % площади между кривой и осью. Возникающая при этом погрешность составляет 0,27% и практического значения не имеет.

При увеличении значение наибольшей ординаты y_max уменьшается, а поле рассеяния возрастает, в результате чего кривая становится более пологой и низкой, что свидетельствует о большом рассеянии размеров и меньшей точности. Следовательно, среднее квадратическое отклонение – мера рассеяния и точности.

По данным непосредственных измерений и расчётов по формуле, погрешность определения среднего квадратического отклонения, обозначаемого в этом случае S, зависит от общего количества n измеряемых заготовок и в отдельных случаях весьма значительна. Учитывая это, для предотвращения возможного появления брака целесообразно при использовании формулы

(4)

принять следующее соотношение:

= pS, (5)

где S – среднее квадратическое отклонение, определяемое на основании данных замеров партии заготовок:

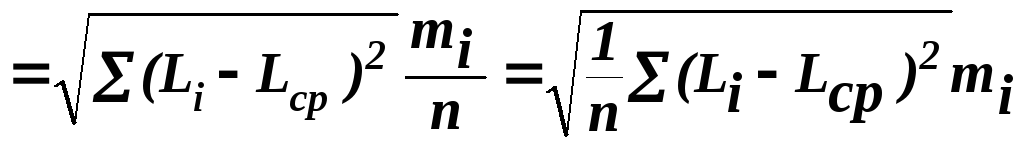; (6)

р – коэффициент, учитывающий погрешность определения среднего квадратического при малых размерах партии измеренных заготовок.

Наибольшая погрешность определения S в процентах к среднему квадратическому генеральной совокупности и значение поправочного коэффициента р при разном числе заготовок представлены в табл. 1.

Таблица 1