2. Силовой расчет механизма в 11ом положении.

1. Определение сил полезного сопротивления и (сил давления газов на поршни).

Согласно данным индикаторных диаграмм находим давление газов на поршни в текущем положении. Методика определения силы полезного сопротивления описана в п. 4.1.1.

Определяем значения сил полезного сопротивления:

,

,

1. Определение сил действующих на звенья механизма.

1. Определяем силы и моменты инерции, действующие на звенья механизма:

Момент инерции определяется по формуле:

2. Определяем веса звеньев механизма:

3. Вычисляем плечи пар сил.

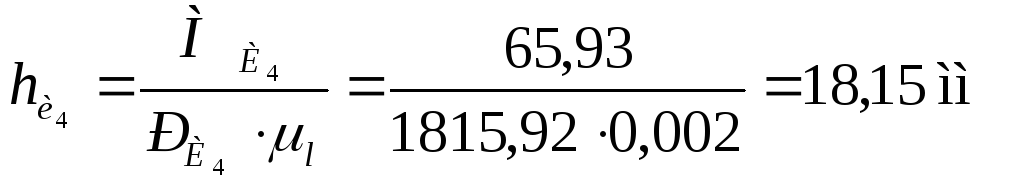
3. Рассмотрим группу Ассура 2-3.

Прикладываем активные (, , ), инерциальные (, ), реактивные (, ) силы и инерциальный момент (), находи точку качания К (см. п. 4.1.3.).

Раскладываем на составляющие (направляем по оси шатуна) и (направляем перпендикулярно оси шатуна). Направление реакции нам известно.

Составив уравнение моментов относительно точки В, определим :

Реакции и находим графически.

Построение силового многоугольника см. п. 4.1.3.

Приняв масштаб сил , определяем величины искомых реакций:

4. Рассмотрим группу Ассура 4-5.

Прикладываем внешние (, , ), инерциальные (, ), реактивные (, ) силы и инерциальный момент (). См. п. 4.1.4.

Определяем точку качания К см. п. 4.1.3.

Раскладываем реакцию , на составляющие (направляем по оси шатуна) и (направляем перпендикулярно оси шатуна). Направление реакции нам известно.

Составив уравнение моментов относительно точки С, определим :

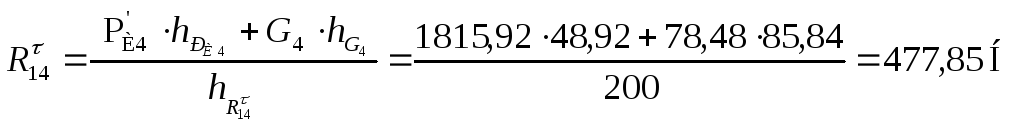
Реакции и находим графически. См. п. 4.1.3.

Приняв масштаб сил , определяем величины искомых реакций:

5. Рассмотрим ведущее звено.

К точке А ведущего звена прикладываем найденный ранее реакции и , и приведенную силу , в точке О прикладываем реакцию опоры (см п. 4.1.5.)

Для определения величины составим уравнение моментов относительно точки О:

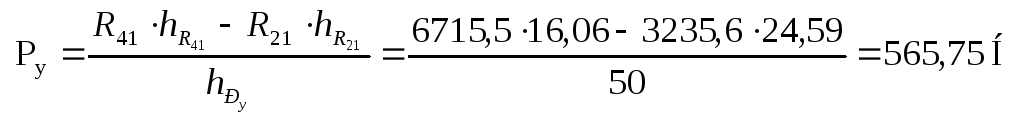
Реакцию опоры найдем графически (способ построения силового многоугольника см. п. 4.1.3).

Приняв масштаб силы , определяем:

6. Построение рычага Жуковского для пятого положения.

Метод построения рычага Жуковского см. п. 4.1.6.

Повернув план скоростей на 90, прикладываем в характерные точки все силы, исключая реактивные. Причем силы и прикладываем в точки качания, которые находятся из пропорций:

Составим уравнение моментов относительно полюса р:

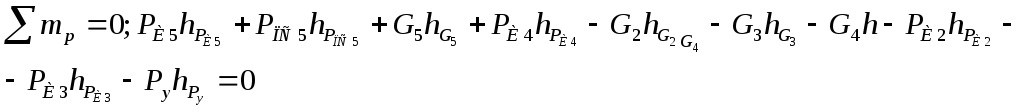
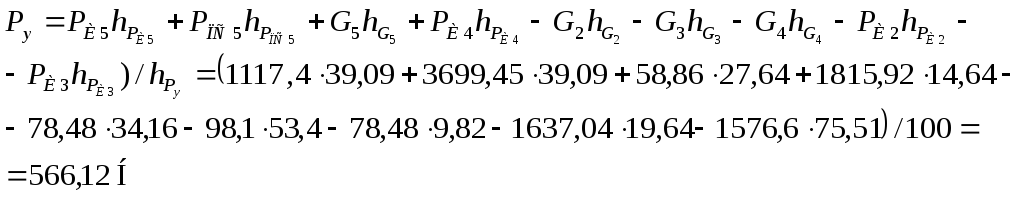
7. Погрешность определения величины приведенных сил, найденных силовым методом и методом Жуковского.

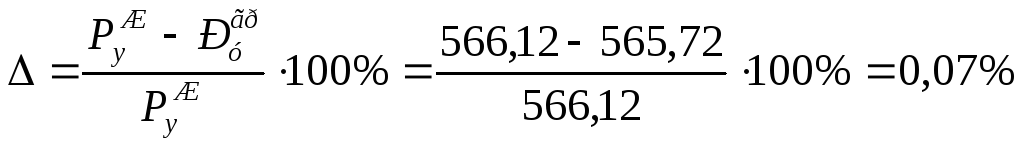
5. Расчет маховика и исследование движения механизма.

5.1. Определим моменты сил сопротивления для каждого положения и строим график M_с=М_с() и строим его в произвольном масштабе _М.

Рассчитываем для остальных положений и заносим в таблицу

Таблица 5.1 – Расчетная таблица приведенного момента сил сопротивления

№ положения	Давление в правом цилиндре р3, кПа	РПС3, Н	VB, м/с	Движение поршня B	Давление в левом цилиндре р5, кПа	РПС5, Н	VС, м/с	Движение поршня C	Мс, Нм
1	0	0	0	НМТ	477	5392,01	9,97		-755,03
2	3	103,86	3,45		657	7426,73	10,22		-1071,02
3	21	726,99	7,05		900	10173,60	6,52		-1003,61
4	63	2180,97	9,97		900	10173,60	0	ВМТ	-305,4
5	162	5608,20	10,22		495	5595,48	6,52		-292,6
6	300	10385,55	6,52		270	3052,08	10,22		-512,94
7	300	10385,55	0	ВМТ	270	3052,08	9,97		427,38
8	114	3946,51	6,52		270	3052,08	7,05		663,6
9	0	0	10,22		270	3052,08	3,45		147,89
10	0	0	9,97		270	3052,08	0	НМТ	0
11	0	0	7,05		288	3255,55	3,45		-157,75
12	0	0	3,45		360	4069,44	7,05		-402,94

По значениям М_С строим график. Принимаем

1. Интегрируя графически график М_с=М_с() получаем график А_с=А_с().

Метод графического интегрирования описан в п. 2.11.

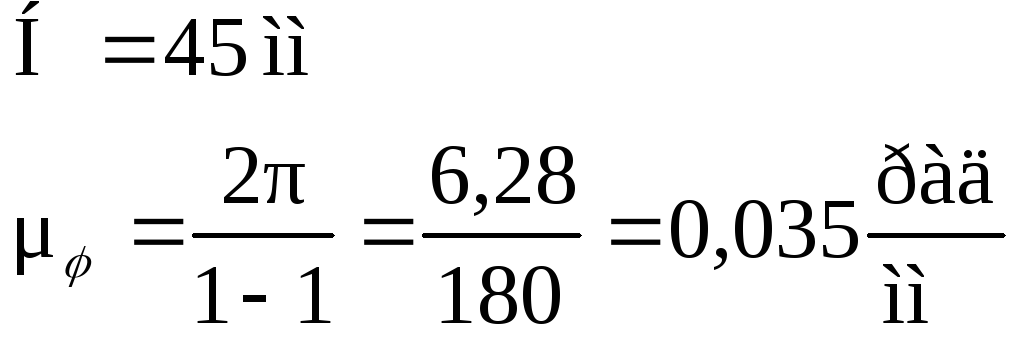
2. Считая момент движущих сил постоянной величиной строим график работ движущих сил за цикл А_Д=А_С.

3. Строим график приращения кинетической энергии, вычитая из ординат графика 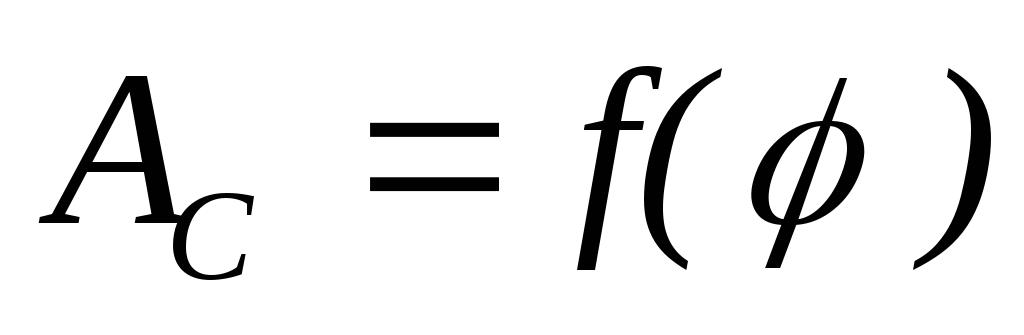соответствующие ординаты графика 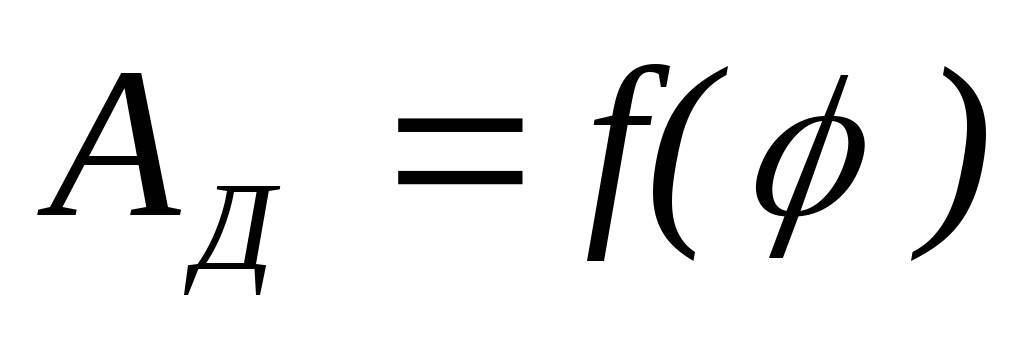и откладываем разность на соответствующей точке оси абсцисс. Получаем график приращения кинетической энергии .

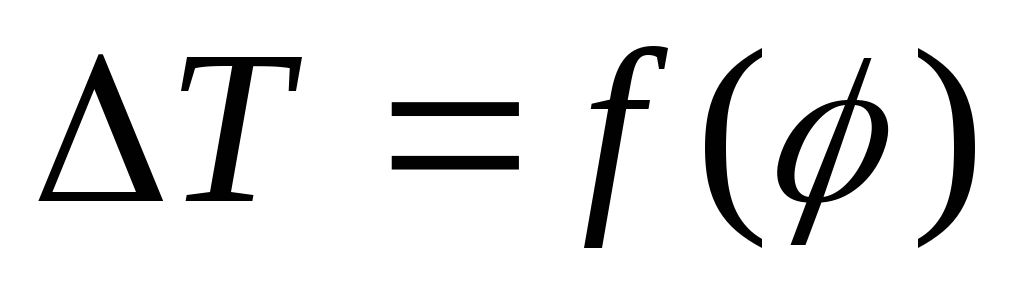4. Строим график приведенных моментов инерции.

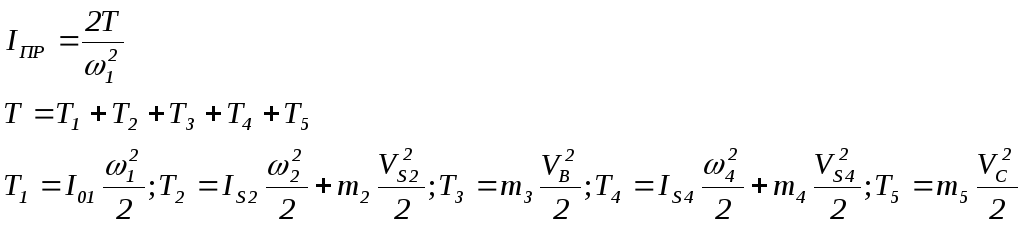
Заносим значения угловых и линейных скоростей в таблицу и рассчитываем I_ПР для каждого положения

Таблица 5.2. – Приведенный момент инерции

№	1	2	3	4	5	6	7	8	9	10	11	12
T1	315,51	315,51	315,51	315,51	315,51	315,51	315,51	315,51	315,51	315,51	315,51	315,51
ω2	12,56	10,96	6,43	0	6,43	10,96	12,56	10,96	6,43	0	6,43	10,96
Vs2	3,52	3,85	4,54	5,025	4,85	4,06	3,52	4,06	4,85	5,025	4,54	3,85
T2	66,73	72,36	86,94	101	98,59	79,00	66,73	79	98,59	101	86,94	72,36
Vb	0	1,96	3,79	5,025	4,91	3,06	0	3,06	4,91	5,025	3,79	1,96
T3	0	19,21	71,82	126,25	120,54	46,82	0	46,82	120,54	126,25	71,82	19,21
ω4	0	6,43	10,96	12,56	10,96	6,43	0	6,43	10,96	12,56	10,96	6,43
Vs4	5,025	4,85	4,06	3,52	4,06	4,85	5,025	4,54	3,85	3,52	3,85	4,54
T4	101,00	98,59	79,00	66,73	79,00	98,59	101,00	86,94	72,36	66,73	72,36	86,94
Vc	5,025	4,91	3,06	0	3,06	4,91	5,025	3,79	1,96	0	1,96	3,79
T5	75,75	72,32	28,09	0	28,09	72,32	75,75	43,09	11,52	0	11,52	43,09
T	558,99	577,99	581,37	609,49	641,73	612,24	558,99	571,37	618,52	609,49	558,16	537,11
Iпр	0,44	0,46	0,46	0,48	0,51	0,49	0,44	0,45	0,49	0,48	0,44	0,43

Строим график в масштабе

5. Строим диаграмму энергомасс.

Сносим соответствующие точки графика приращения кинетической энергии до пересечения с графиком приведенного момента инерции. Соединив последовательно точки пересечения получим диаграмму энергомасс в масштабе и .

6. Определяем момент инерции маховика по методу Виттенбауэра.

Определим углы и

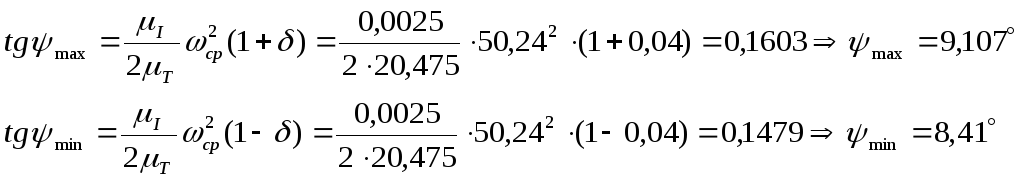
Проводим касательные к верхней и нижней точкам диагрммы энергомасс под углами и соответственно до пересечения с осью . Получаем отрезок (ml)

7. Определяем размеры маховика.

– объемный вес материала маховика (сталь)

8. Определяем истинную угловую скорость.

,

где – абсцисса i-ой точки

– ордината i-ой точки

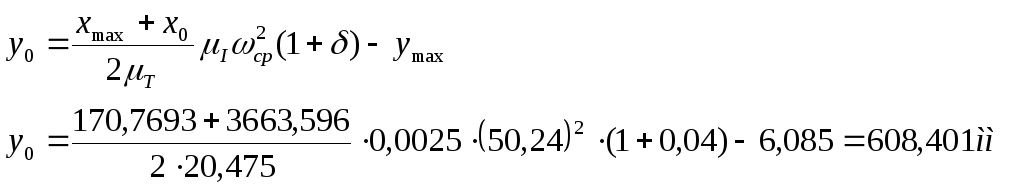
где х_max и у_max абсцисса и ордината точки касания касательной к верхней точке графика, наклоненной под углом к горизонтали.

Определяем координаты точек и заносим в таблицу.

Таблица 5.3.

Определение истиной угловой скорости

	1	2	3	4	5	6	7	8	9	10	11	12
yi	608,40	595,43	580,98	575,11	574,02	570,78	573,54	585,74	601,88	609,61	614,11	614,29
xi	3840,77	3846,79	3847,86	3856,77	3866,99	3857,65	3840,77	3844,69	3859,64	3856,77	3840,50	3833,83
ωi	50,94	50,35	49,73	49,42	49,31	49,23	49,46	49,96	50,54	50,88	51,18	51,23

9. Строим график отклонения угловых скоростей ведущего звена.

9. Графическим дифференцированием строим график аналога угловых ускорений ведущего звена в масштабе

.

Список используемой литературы

1. Артоболевский И.И. Теория механизмов. – М.: Наука, 1988.-640 с.

2. Теория механизмов и механика машин /А.Н. Мамаев, Т.А. Балабина. – М.: Издательство «Экзамен», 2008. – 254с.

3. Курсовое проектирование по теории механизмов и машин /Под ред. В. Н. Екшибаров, И.В. Левищев. – Барнаул: Изд-во АГАУ, 2008. – 94с.

29