47.Пропускная способность mimo канала связи
,
бит/(с×Гц) - пропускная способность
гауссовского канала
,
бит/с - пропускная способность гауссовского
канала
- частота передачи сообщений
,
бит/(с×Гц) – пропускная способность
независимых каналов
- известна точно
-
разложение по сингулярным числам
-
унитарные матрицы размером
соответственно
-
свойство унитарных матриц
-
диагональная матрица сингулярных чисел
размером
,
- ранг матрицы
,
число ненулевых сингулярных чисел
- для независимых и одинаково распределенных
Умножим
обе части на матрицу
:
-
вектор некоррелированных случайных
величин, статистически идентичных
вектору
- вектор гауссовских шумов, статистически
идентичных вектору шумов
→ число
независимых каналов передачи = рангу
матрицы
,
бит/(с×Гц) - пропускная способность для
фиксированной матрицы
-
отношение сигнал-шум
-
полная мощность сигнала, излученного
всеми передатчиками.
Пропускная способность MIMO канала связи
-
ковариационная матрица сообщения
-
след матрицы
,
- мощность шума,
- единичная
матрица
Определение:
- пропускная способность MIMO
канала связи
-
энтропия принимаемого сигнала
-
условная энтропия
-
плотность распределения вероятностей
-
условная плотность
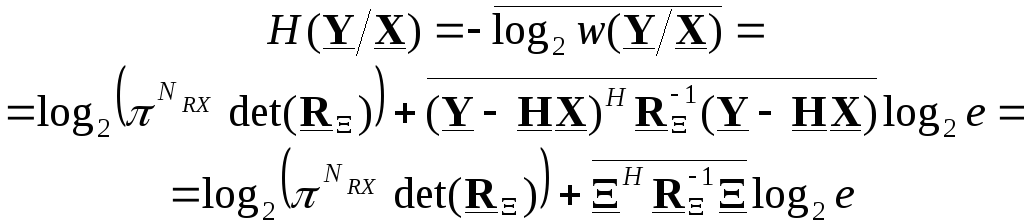
Пропускная способность MIMO канала равна:
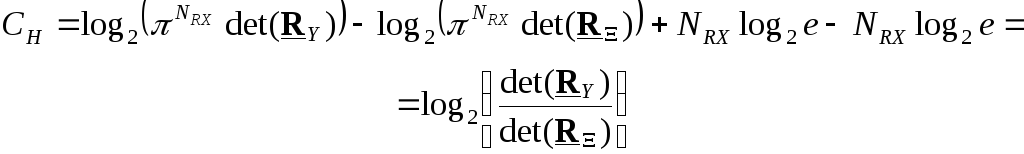Корреляционная
матрица:
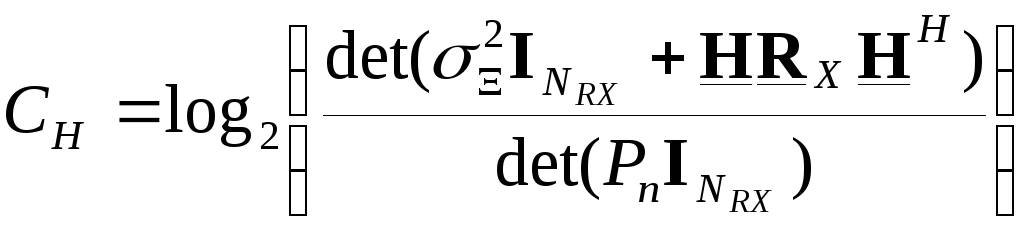
48. Согласование канала и передаваемого сообщения
-
матрица собственных векторов
-
диагональная матрица собственных
значений.
Режим OLTD:
→
Режим CLTD:
-
матрица собственных векторов
-
диагональная матрица собственных
значений.
Условие
максимума пропускной способности
!
-
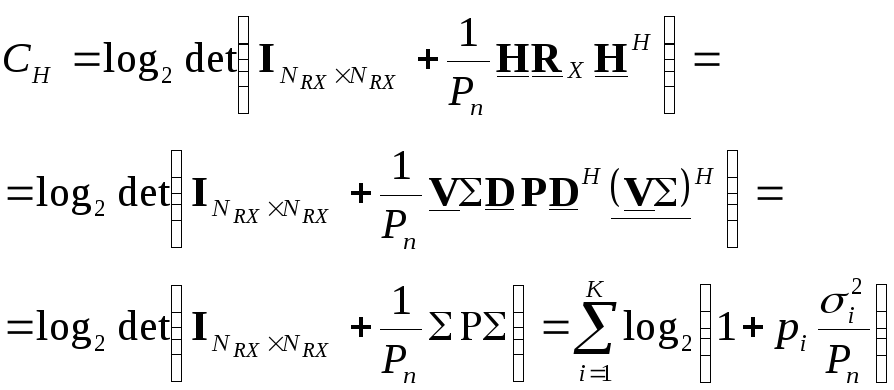
? Метод
«водозаполнения»
(water
filling)
, 
:
-
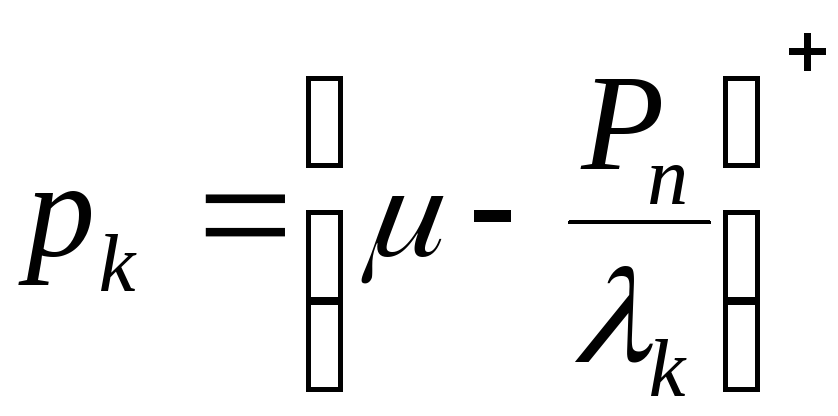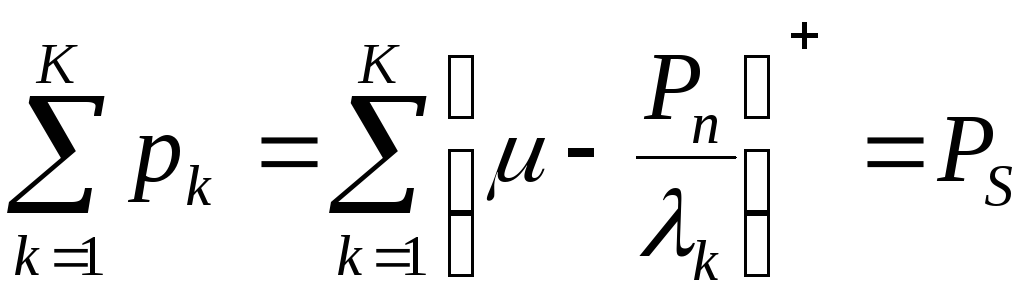
собственные значения матрицы
при
,
или матрицы
при
-
максимальная пропускная способность
Эквивалентное
выражение:
,
.
49.Пространственное кодирование и декодирование методом BLASTДля реализации высокой пропускной способности MIMO-системы связи предложена (Fuschini, 1996) архитектура под названием BLAST (Bell Laboratory Layered Space Time Architecture). Исходная D-BLAST версия использует связь цикла потока данных, называемых уровнями, с передающими антеннами, формируя таким образом единый усредненный канал для всех уровней. Трудности реализации D-BLAST привели к появлению модификации, известной под названием V-BLAST, в которой каждый уровень связан с определенной передающей антенной.
Для выделения информационного сигнала на фоне других сигналов, являющихся для первого мешающими, используются следующие методы:
- обнуления (ZF – zero forcing);
- минимума среднего квадрата ошибки (MMSE – minimum mean-square error).
Метод
BLAST
позволяет увеличить пропускную
способность, а также значительно
упростить обработку принимаемых
сигналов. В этом случае на каждом такте
каждой антенной передается свой
собственный информационный символ (
).
Таким образом, за 1 такт передается
символов. На приемной стороне необходимо
определить, какой из символов передан
каждой из передающих антенн. Если каждая
антенна может передавать
различных символов, то число возможных
комбинаций составляет
,
что существенно увеличивает время
декодирования.
Например,
при
.
В зависимости от способа пространственного кодирования различают:
-
D-BLAST,
в котором используется блочное кодирование
;
-
X-BLAST,
в котором используется демультиплексирование
потока входных данных на
передающих антенн; пространственное
кодирование осуществляется путем
воздействия случайной канальной матрицей
на излучаемый сигнал;
-
V-BLAST
(вертикальный), при котором осуществляется
обработка принимаемого сигнала поочередно
для каждой из передающих антенн с
последующим вычитанием принятого
сигнала. Принят определенный порядок
демодуляции
,
в соответствии с которым производится
демодуляция символов, передаваемых
каждой из
антенн. При этом последовательно
вычисляются статистики
,
которые затем квантуются в КАМ-демодуляторе.
Рассмотрим
случай одного пользователя, хотя метод
BLAST
может быть применен и для случая
нескольких пользователей. Исходный
поток данных мультиплексируется на
потоков, называемых уровнями (layer),
для каждой из передающих антенн.
Формально
алгоритм BLAST
записывается следующим образом. На
первом шаге декодирования
полагаем
.
На
каждом последующем
-м
шаге рассчитывается матрица «обнуления»
в виде псевдоинверсии матрицы
:
где
обозначает комплексное сопряжение и
транспонирование матрицы
.
Выбор
уровня для обнуления производится,
начиная с уровня, имеющего наибольшее
значение отношения сигнал-шум, что
соответствует выбору одной из
-й
строк
матрицы
с минимальной нормой и определению
соответствующей строки как вектора
«обнуления» на данном шаге:
В
соответствии с методом обнуления вектор
весовых коэффициентов должен удовлетворять
условию
,
что соответствует значению
,
где
-
-я
строка матрицы
.
Путем
умножения
на вектор принятого сигнала
происходит подавление всех уровней,
кроме одного, передаваемого антенной
.
В результате получаем статистику для
принятия решения:
Полученный
-й
уровень может быть обнаружен на множестве
сигнального созвездия
:
Аналогично первому уровню обнаруженного уровня можно улучшить процесс обнаружения на последующих уровнях. Вычитая часть обнаруженного сигнала из вектора принятых сигналов, уменьшаем на 1 число уровней, которые необходимо обнулить на последующих шагах. Принимаемый сигнал преобразуется следующим образом:
Внутри
канальной матрицы
-й
столбец
в дальнейшем не нужен и удаляется:
Таким
образом, матрица
получена обнулением
столбцов матрицы
.
Далее
процесс обнаружения повторяется для
,
пока не обнаружатся все уровни, т.е.
.
Теоретически на каждом шаге обнаружения число обнаруживаемых сигналов уменьшается, в то время как число приемных антенн остается прежним. Однако степень разнесения результирующей системы должен увеличиваться от уровня к уровню.