
- •Лекция № 12 « Предел функции» п.1. Предел функции на бесконечности
- •Предел функции в точке
- •Бесконечно малые функции и их основные свойства.
- •Основные свойства бесконечно малых функций
- •Свойства бесконечно больших величин
- •Соотношение между бесконечно малыми и бесконечно большими функциями
- •Основные теоремы о пределах. Признаки существования предела.
- •Замечательные пределы
- •Сравнение бесконечно малых величин.
Соотношение между бесконечно малыми и бесконечно большими функциями
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Примеры.
-
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
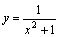 –
бесконечно малая при x→+∞,
т.е.
–
бесконечно малая при x→+∞,
т.е.
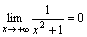 .
.
-
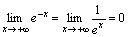 .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Примеры.
-
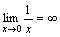 .
.
-
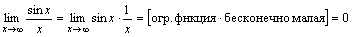 .
.
-
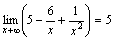 ,
так как функции
,
так как функции
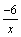 и
и
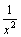 -
бесконечно малые при x→+∞,
то
-
бесконечно малые при x→+∞,
то
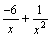 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
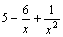 является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]() .
.
Основные теоремы о пределах. Признаки существования предела.
-
Функция не может иметь более одного предела.
-
Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
![]()
Пример.
![]() .
.
3. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
![]() .
.
Следствие 2. Предел степени равен степени предела:
![]() .
.
Пример:
![]() .
.
-
Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
Примеры.
1.)
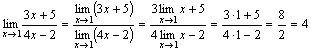 .
.
2.)
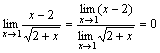 .
.
3.)Рассмотрим
![]() .
При x→1
числитель дроби стремится к 1, а знаменатель
стремится к 0. Но так как
.
При x→1
числитель дроби стремится к 1, а знаменатель
стремится к 0. Но так как
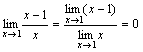 ,
т.е.
,
т.е.
![]() есть
бесконечно малая функция при x→1,
то
есть
бесконечно малая функция при x→1,
то
![]() .
.
5. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
![]() ,
то
,
то
![]() .
.
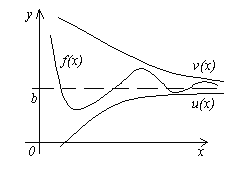
Смысл этой теоремы понятен из рисунка.
6.
Если
две функции f(x)
и
g(x)
при всех значениях аргумента x
удовлетворяют неравенству f(x)≥
g(x)
и имеют пределы
![]() ,
то имеет место неравенство b≥c.
,
то имеет место неравенство b≥c.
Замечательные пределы
Первым
замечательным пределом называется
![]()
Вторым замечательным
пределом:
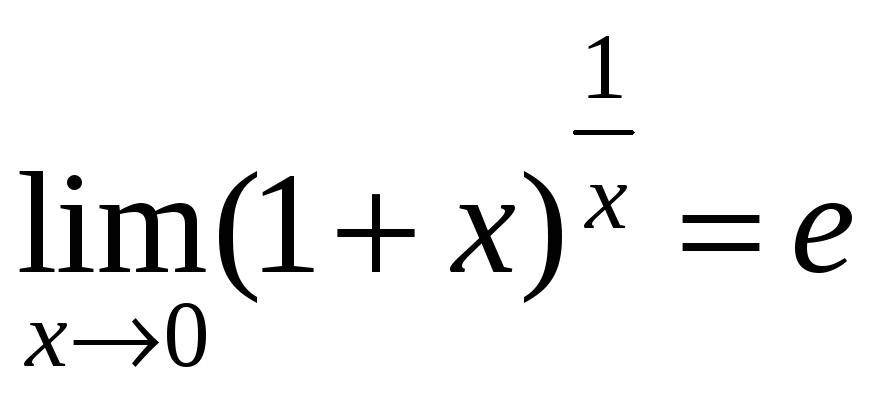 или
или
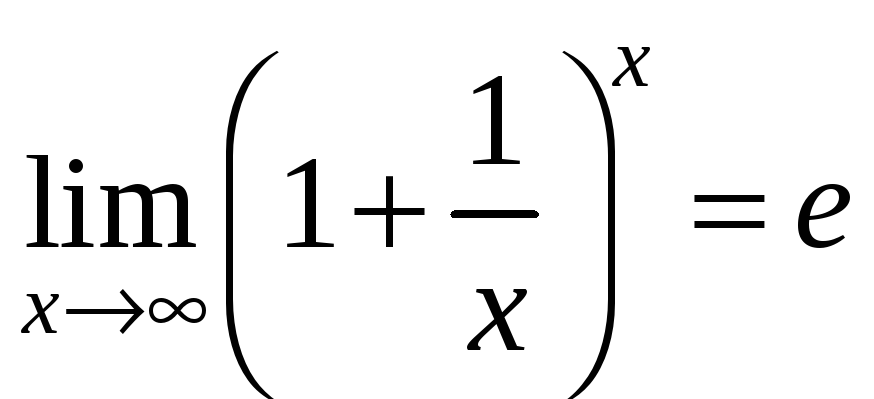
Число
![]() .
Точнее
.
Точнее
![]() …,
т.е является числом иррациональным.
Играет весьма важную роль в математическом
анализе. Широко используются логарифмы
по основанию
…,
т.е является числом иррациональным.
Играет весьма важную роль в математическом
анализе. Широко используются логарифмы
по основанию
![]() ,
называемые натуральными.
,
называемые натуральными.
Сравнение бесконечно малых величин.
Как известно сумма, разность и произведение двух бесконечно малых функций есть функция бесконечно малая. Отношение же двух б\м ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, б\м ф. или вообще не стремиться ни к какому пределу.
Две б\м ф. сравниваются между собой с помощью их отношения.
Пусть
![]() и
и
![]() есть б\м
ф. при
есть б\м
ф. при
![]() .
.
Рассмотрим их отношение. 1
Выделим 4 случая:
1)
если
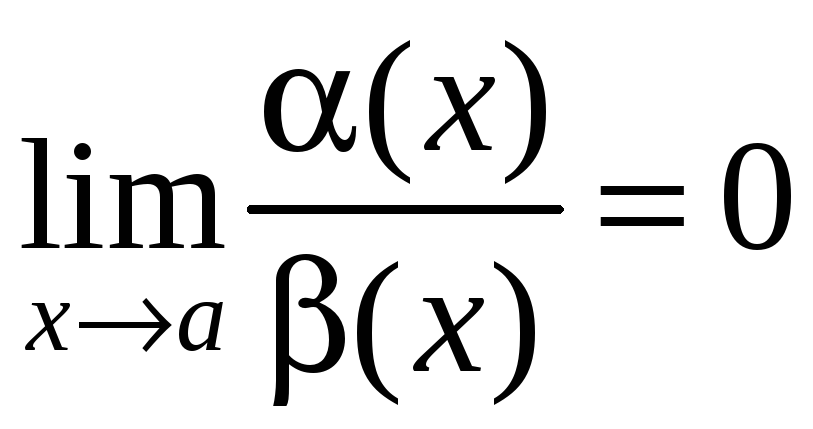 .
В этом случае говорят, что
.
В этом случае говорят, что
![]() - бесконечно малая более высокого
порядка, чем
- бесконечно малая более высокого
порядка, чем
![]() .
.
Пример:
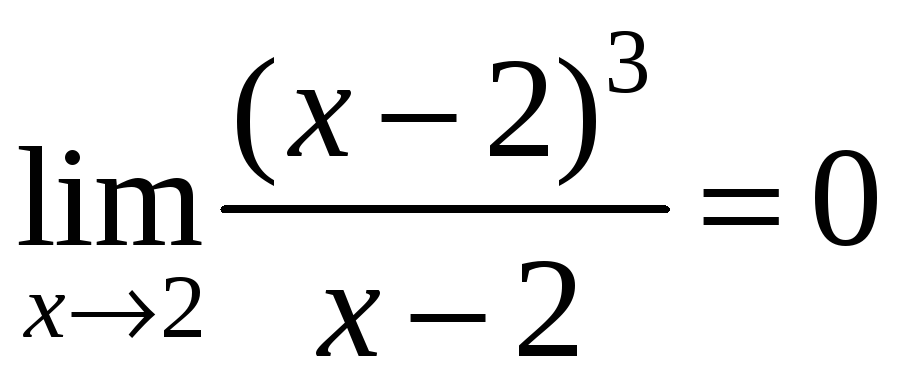 ,
т.е.
,
т.е.
![]() бесконечно малая более высокого порядка
чем
бесконечно малая более высокого порядка
чем
![]() .
.
2)
если
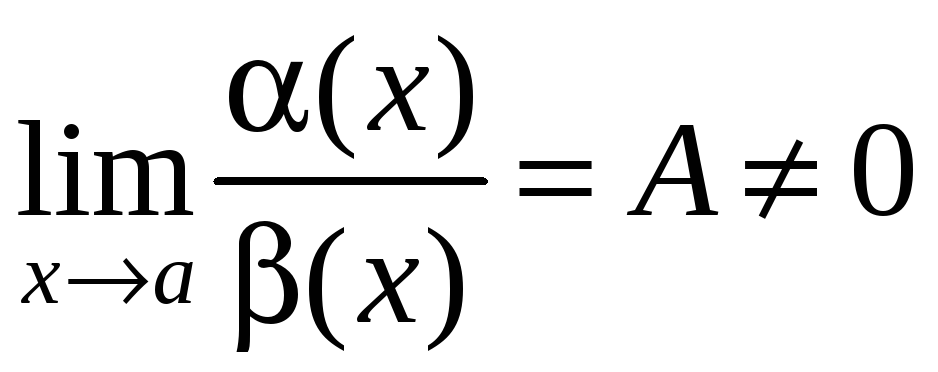 (где
(где
![]() -
число). В этом случае функции называются
б\м одного и того же порядка.
-
число). В этом случае функции называются
б\м одного и того же порядка.
Пример:
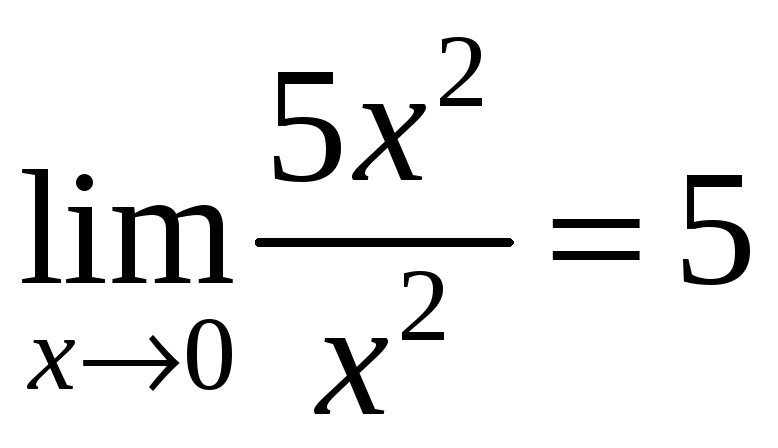 ,
т.е
,
т.е
![]() и
и
![]() являются б\м одного порядка малости.
являются б\м одного порядка малости.
3)
если
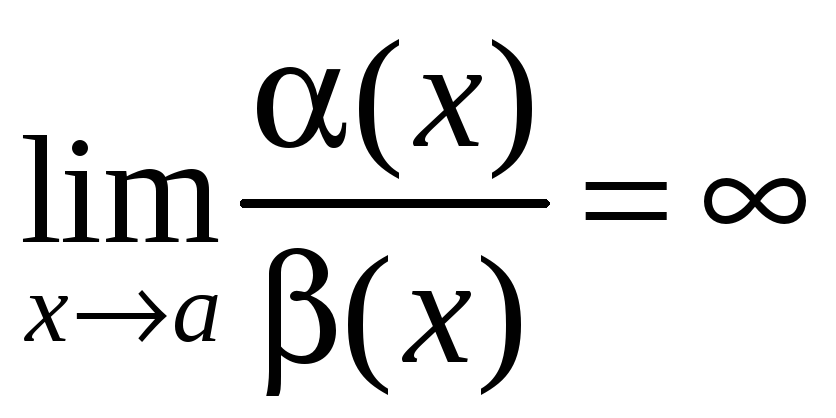 в этом случае говорят, что
в этом случае говорят, что
![]() -
бесконечно малая более низкого порядка,
чем
-
бесконечно малая более низкого порядка,
чем
![]() .
.
Пример:
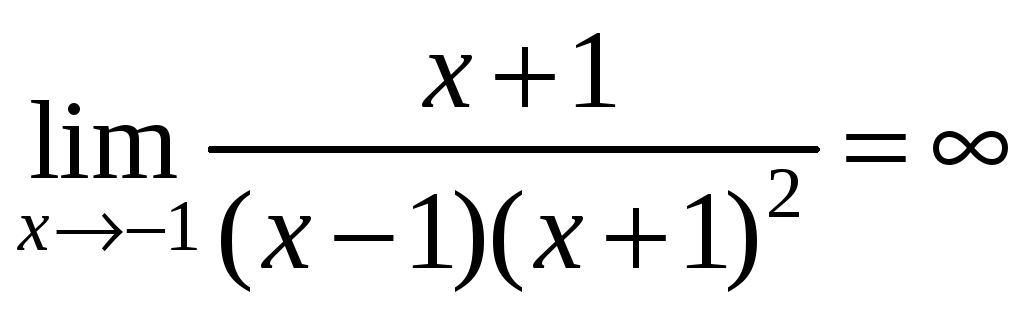 ; при
; при
![]()
![]() б\м более низкого порядка чем
б\м более низкого порядка чем
![]()
4)
если
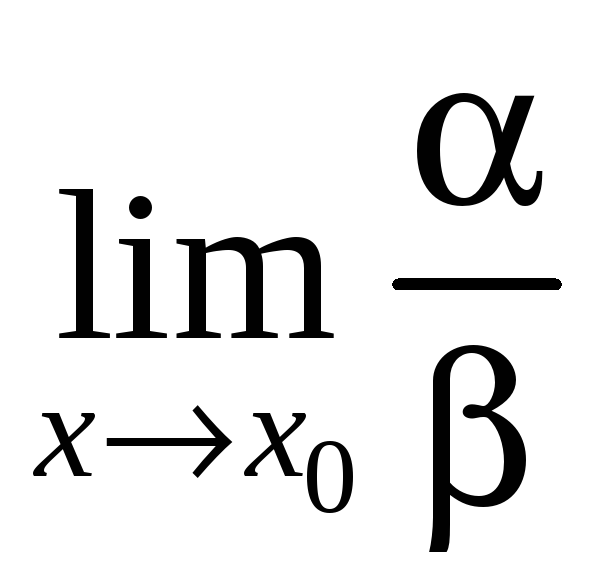 не существует, то
не существует, то
![]() и
и
![]() называются несравнимыми бесконечно
малыми функциями.
называются несравнимыми бесконечно
малыми функциями.
Пример:
Можно ли сравнить функции
![]() и
и
![]() при
при
![]() ?
?
Нет, т.к. предел
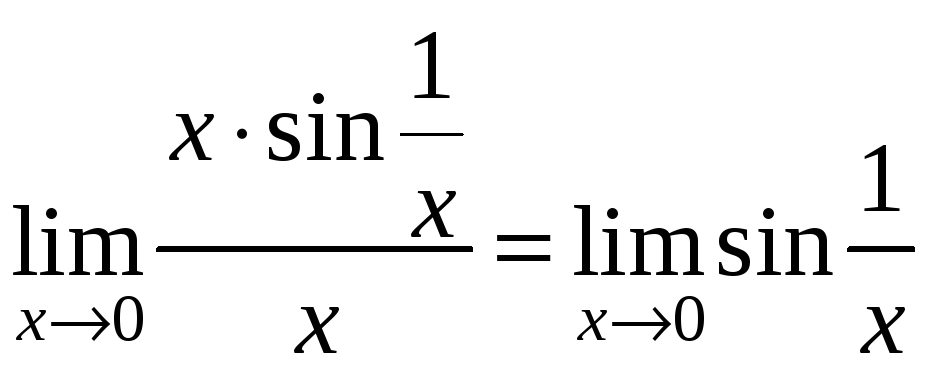 не существует.
не существует.
А теперь про самое главное:
Определение:
Если функции
![]() и
и![]() б\м одного и того же порядка, причем
б\м одного и того же порядка, причем
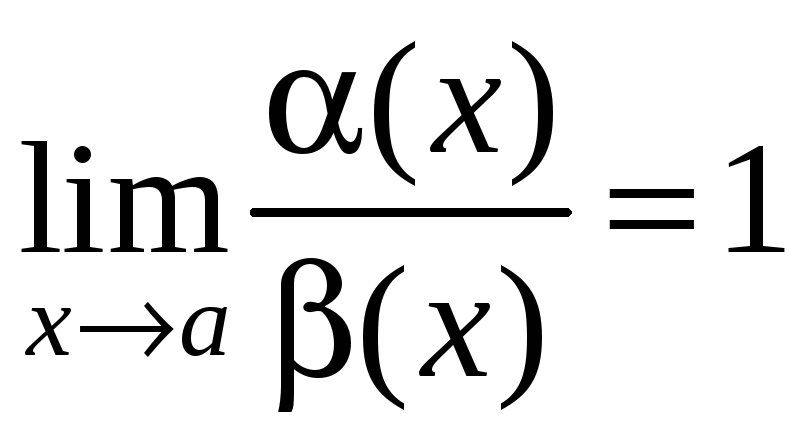 ,
то они называются эквивалентными б\м.
,
то они называются эквивалентными б\м.
Символически это
записывают так:
![]() .
.
![]() или
или
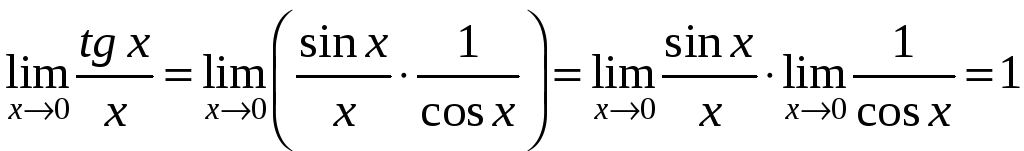 таким образом
таким образом
![]() и
и
![]() ,
,
![]() и
и
![]() являются эквивалентными б\м.
являются эквивалентными б\м.
Теорема:
Если существует предел отношения двух
бесконечно малых функций
![]() и
и![]() ,
то он равен пределу отношения
соответствующих им эквивалентных
бесконечно малых.
,
то он равен пределу отношения
соответствующих им эквивалентных
бесконечно малых.
Теорема: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.
Т.е
![]() или
или
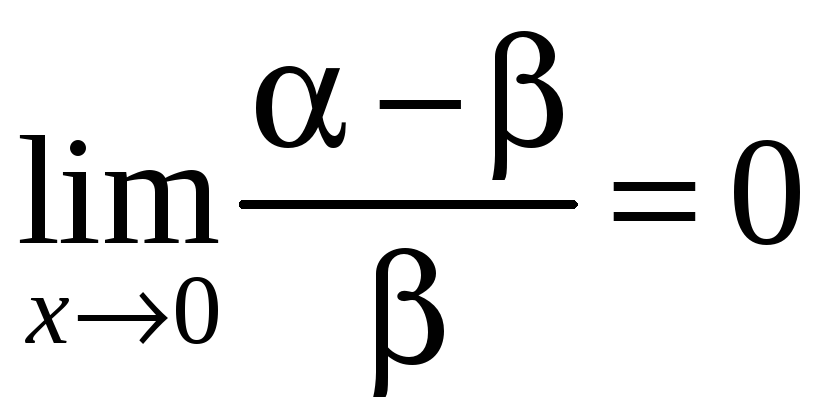
Справедливо и
обратное утверждение: если разность
б.м.ф.
![]() и
и![]() есть бесконечно малая высшего порядка,
чем
есть бесконечно малая высшего порядка,
чем
![]() и
и![]() ,
то
,
то
![]() и
и![]() эквивалентные б.м.ф.
эквивалентные б.м.ф.
Теорема: Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.
Пример:
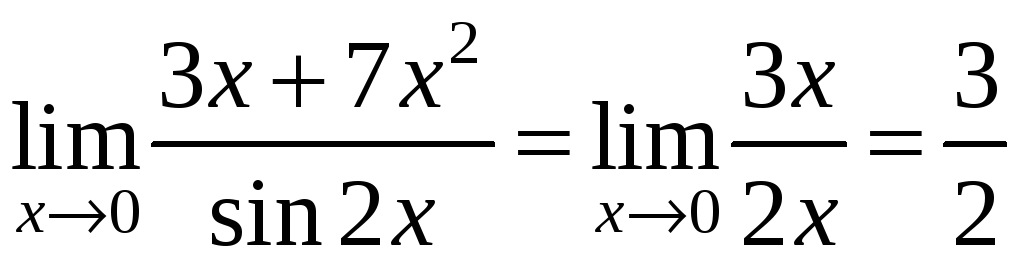
Примеры на практике!
Таблицы эквивалентных бесконечно малых в любом справочнике.
