Бесконечно малые функции и их основные свойства.

ОПРЕДЕЛЕНИЕ: Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

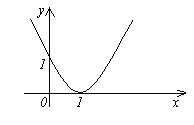
1. Функция является бесконечно малой при x→1, так как (см. рис.).

2. 

2. Функция f(x) = tgx – бесконечно малая при x→0.

3. f(x) = ln (1+x)– бесконечно малая при x→0.

4. f(x) = 1/x– бесконечно малая при x→∞.

Связь бесконечно малых величин с пределами функций.

Теорема: Если функция имеет при x→a или при x→∞, предел равный ., то ее можно представить в виде суммы этого числа и бесконечно малой при x→a или при x→∞.

Доказательство:

Докажем теорему для случая x→a. По условию функция имеет предел и . Это означает: что если для любого, даже сколь угодно малого положительного числа, найдется такое положительное число ( зависящее от ,), что для всех и удовлетворяющих неравенству:

Выполняется

Или обозначив , имеем . А это собственно и значит, что - бесконечно малая величина. А из

.

Верна и обратная теорема:

Теорема: Если функцию можно представить как сумму числа и бесконечно малой при x→a или при x→∞, то число есть предел этой функции при x→a или при x→∞, т.е. .

Основные свойства бесконечно малых функций

1. Теорема 1: Алгебраическая сумма (разность) двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

2. Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Из доказанной теоремы вытекают:

Следствие 1. Если и

То .

Следствие 2. Если и c=const, то

3. Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть . Тогда 1/f(x) есть ограниченная функция. Поэтому дробь есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

ОПРЕДЕЛЕНИЕ: Функция называется бесконечно большой величиной при , если для любого, даже сколь угодно большого положительного числа , найдется такое положительное число ( зависящее от , ) , что для всех и удовлетворяющих условию , будет верно неравенство .

Обозначение:

Например: при бесконечно большая функция. при бесконечно большая функция, причем , и

Определение бесконечно большой величины при запишем в краткой форме, его записать самим подробно!

или , обе функции являются бесконечно большими.

Не следует путать бесконечно большую переменную величину с очень большим , но постоянным числом , т.к. по мере приближения значений к или по мере увеличения по модулю (при ) в соответствии с , функция превзойдет это число ( по абсолютной величине).

Свойства бесконечно больших величин

1. Произведение б\б величины на функцию, предел которой отличен от нуля, есть величина б\б .

2. Сумма б\б величины и ограниченной функции есть величина б\б .

3. Частное от деления б\б величины на функцию, имеющую предел, есть величина б\б .

Например:

1. если есть б\б величина при , функция при имеет предел , то функция - б\б. (1 свойство)

2. Если есть б\б величина при и - ограниченная функция, то - б\б функция ( 2 свойство)

3. является б\б функцией при . ( свойство 3)