Лекция № 12 « Предел функции» п.1. Предел функции на бесконечности

С понятием предела числовой последовательности тесно связано понятие предела функции в бесконечности. Если в случае последовательностей переменная , возрастая принимает лишь целые значения, то во втором случае переменная , изменяясь, принимает любые значения.

ОПРЕДЕЛЕНИЕ: Число называется пределом функции при , стремящимся к бесконечности, если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число

( зависящее от ,), что для всех таких, что , выполняется неравенство:

Этот предел функции обозначается .

Смысл определения: при достаточно больших по модулю значениях , значения функции как угодно мало отличаются от числа ( по абсолютной величине).

Геометрический смысл предела функции в бесконечности:

Неравенство равносильно двойному неравенству , соответствующему расположению части графика в полосе шириной (см. рис.)

Рис.2.5.Предел при

ИТАК: число есть предел функции при , если для любого найдется такое число , что для всех , соответствующие ординаты графика функции будут заключены в полосе , какой бы узкой эта полоса не была.

Пример: Доказать, что

Решение: Выясним, для каких будет выполняться неравенство .

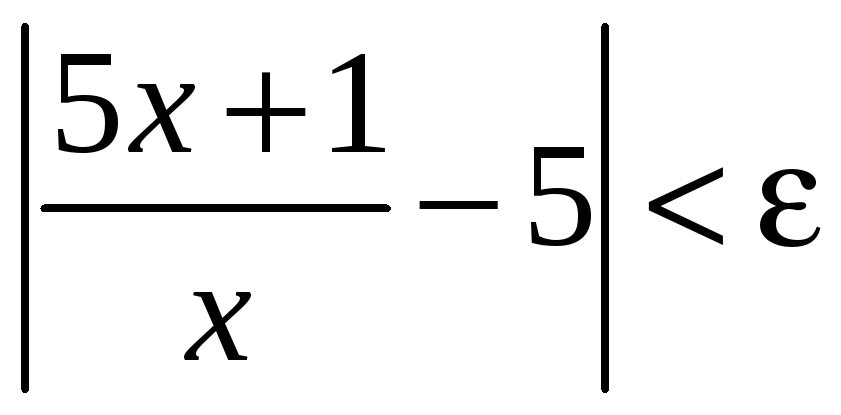После проведенных преобразований получаем : и .

Таким образом, нашли каким должно быть число ,, и для всех , будет верно неравенство . Чем меньше , тем больше значение , после которого все значения функции лежат в выбранной полосе, шириной .

Данное определение предела предполагает неограниченное возрастание независимой переменной по абсолютной величине. В то же время можно сформулировать определение предела при стремлении к бесконечности определенного знака, т.е. при и при . В первом случае основное неравенство должно выполняться для всех таких, что , а во втором- для всех таких, что .

Предел функции в точке

Пусть функция задана в некоторой окрестности точки , кроме, быть может, самой точки (иначе: функция определена в проколотой окрестности точки ).

ОПРЕДЕЛЕНИЕ(по Коши): Число называется пределом функции при ( или в точке ), если для любого, даже сколь угодно малого положительного числа, найдется такое положительное число ( зависящее от ,), что для всех и удовлетворяющих неравенству:

Выполняется

Обозначается:

Смысл определения предела функции в точке : для всех значений , достаточно близких к , значение функции как угодно мало отличается от числа (по абсолютно величине).

Геометрический смысл предела функции в точке:

Уже говорилось, что неравенство равносильно двойному неравенству , которое соответствует расположению части графика в полосе шириной. Аналогично неравенство равносильно двойному неравенству, соответствующему попаданию точек в - окрестность точки .

ИТАК: число есть предел функции при , если для любого найдется такая - окрестность точки , что для всех , из этой окрестности соответствующие ординаты графика функции будут заключены в полосе , какой бы узкой она ни была.

Пример: Доказать, что

Замечание: Определение предела не требует существования функции в самой точке , т.к. рассматривает значения в некоторой окрестности точки .

Другими словами, рассматривая предел функции в точке , мы предполагаем, что стремится к , но не достигает значения . Поэтому наличие, или отсутствие предела при определяется поведением функции в окрестности точки , но не связано со значением функции (или его отсутствием) в самой точке.

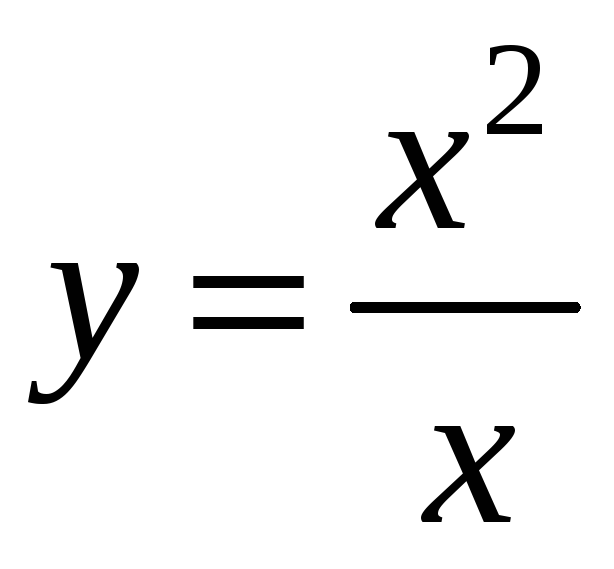Пример: Предел функции в точке a = 0 равен 0: Предел функции в точке a = 0 также равен 0, хотя эта функция не существует в этой точке (ее знаменатель обращается в нуль).

Предел функции 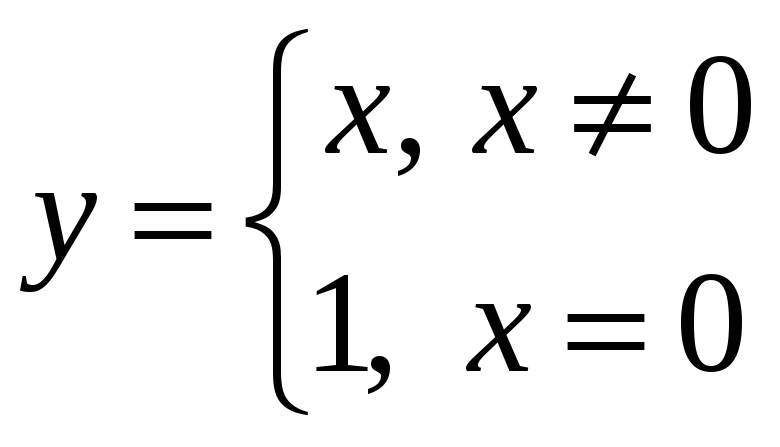в точке a = 0 равен 0, хотя значение функции в этой точке f (0) = 1.

Замечание 2: Если при стремлении к , переменная принимает лишь значения, меньшие , и при этом функция стремится к некоторому числу , то говорят об односторонних пределах функции.

ОПРЕДЕЛЕНИЕ: Число A₁ называется пределом функции f (x) слева в точке a, если для каждого существует δ > 0 такое, что для всех выполняется неравенство  

Число A₂ называется пределом функции f (x) справа в точке a, если для каждого существует δ > 0 такое, что для всех выполняется неравенство .

Предел слева обозначается предел справа – . Эти пределы характеризуют поведение функции слева и справа от точки a.

В обозначении односторонних пределов при x → 0 обычно опускают первый нуль: и .

Так, для функции

; 

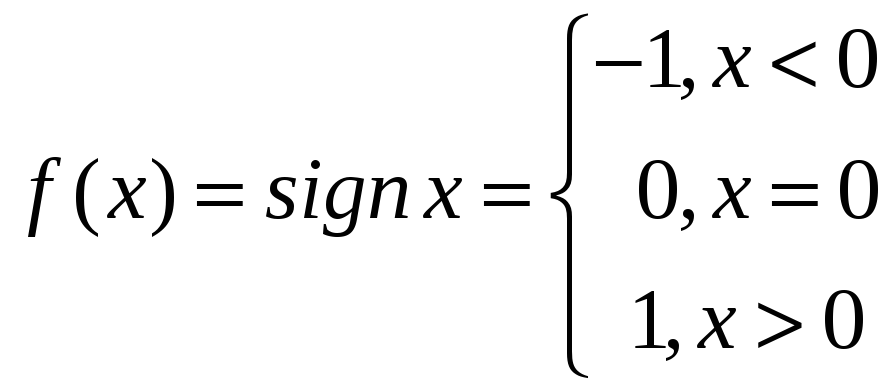
Запишем определение предела функции в терминах последовательностей:

ОПРЕДЕЛЕНИЕ( по Гейне): Число называется пределом функции в точке , если эта функция определена в некоторой окрестности точки за исключением, быть может, самой точки , и для любой последовательности такой, что сходящейся к числу , соответствующая последовательность значений функции сходится к числу .

Практика на семинаре!