7.8. Деякі застосування в економіці.

7.8.1. Витрати, доход та прибуток.

Нехай буде функцією загальних витрат на виробництво одиниць продукції, - функція маргінальних витрат яку називають гранично можливі витрати в умовах хоча би постійного відтворення виробництва відповідної продукції. Тоді визначений інтеграл дорівнює зміні загальних витрат при зростанні кількості виробленої продукції від до одиниць. Звідси випливає важливий наслідок:

Зміна виробничих витрат при зростанні виробленої продукції від до одиниць дорівнює площі криволінійної трапеції, обмеженої графіком функцій маргінальних витрат , відрізком та прямими та .

Аналогічно, якщо та - функції маргінального доходу та прибутку відповідно, то зміни доходу та прибутку при зростанні реалізації виробленої продукції від до одиниць обчислюються за формулами .

Приклад: Функція маргінальних витрат фірми має вигляд . Знайти зростання загальних витрат, коли виробництво зростає з 1000 до 1500 одиниць.

Розв’язування: За формулою зростання загальних витрат буде

. Отже, витрати зростуть на 5500 гривень.

7.8.2. Коефіцієнт нерівномірного розподілу прибуткового податку.

Нехай є частина загального прибуткового податку пропорційна частині усього населення держави.

Наприклад, якщо , а , то це означає, що 50% населення сплачує 25% загального прибуткового податку.

Якщо , коли , то це означає, що 90% населення сплачує 70% прибуткового податку. У загальному випадку та - дробові частини цілого і є функцією , тобто .

Будемо вважати, що немає осіб, які не сплачують прибуткового податку, тобто і весь прибутковий податок сплачує 100% населення, тобто .

Г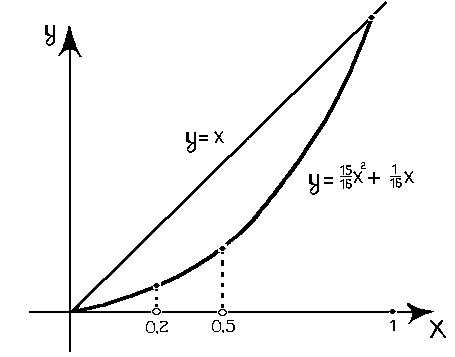рафік функції , яка описує дійсний розподіл прибуткового податку, називають кривою Лоренца. Припустимо, що крива Лоренца задана рівнянням (див.рис.).

Коли , маємо . Це означає, що 20% населення сплачує 5% загального податку. Коли , маємо . Це означає, що 50% населення сплачує тільки 25,56% податку.

Коефіцієнтом нерівності розподілу податку кривої Лоренца називають відношення площі фігури, обмеженої кривою Лоренца та прямою (на рис. вона заштрихована) до площі фігури, що лежить нижче прямої (на рис. – це прямокутний трикутник: ). Коефіцієнт нерівного розподілу податку, що здійснюється за законом Лоренца, позначають .

Площа трикутника . Площу заштрихованої фігури одержимо з використанням визначеного інтеграла за формулою . Тому, згідно з означенням, коефіцієнт Лоренца обчислюють за формулою .

У випадку кривої Лоренца вигляду коефіцієнт нерівності розподілу податку буде

. Відмітимо, що коефіцієнт нерівності розподілу податку завжди задовольняє співвідношення . Коли , прибутковий податок розподілено рівномірно, коли , нерівномірність розподілу податків найбільша.

7.8.3. Максимізація прибутку за часом.

Нехай та - загальні витрати, доход та прибуток, що змінюються з часом, тобто залежать від часу . Тоді або . Максимум загального прибутку буде тоді, коли або . Іншими словами, існує такий час , коли , тобто швидкості зміни доходу та витрат рівні (див.рис.). Загальний прибуток за час можна знайти за формулою . З рис. бачимо, що максимум прибутку дорівнює площі між кривими та на проміжку (заштрихована частина).

Приклад: Швидкості зміни витрат та доходу підприємства після початку його діяльності визначилися формулами та , де і вимірювались роками. Визначити, як довго підприємство було прибутковим та знайти загальний прибуток, який було одержано за цей час.

Розв’язування. Оптимальний час для прибутку підприємства одержимо з умови : . Отже, підприємство було прибутковим 8 років. За цей час було одержано прибутку

(млн.грн.).