
- •Вступ Невизначений і визначений інтеграли.
- •Розділ 6. Невизначений інтеграл.
- •6.1. Первісна та її властивості.
- •6.2. Невизначений інтеграл і його властивості.
- •6.6. Основні методи інтегрування.
- •6.6.1. Метод безпосереднього інтегрування.
- •6.6.2. Метод підстановки (заміни змінної).
- •6.6.3. Метод інтегрування частинами.
- •Рекомендації до застосування методу інтегрування частинами.
- •6.6.4. Інтегрування раціональних дробів.
- •6.6.5. Інтегрування виразів, що містять ірраціональності.
- •6.6.6. Інтегрування деяких тригонометричних виразів.
- •6.6.8. Раціональна функція від .
- •Розділ 7. Визначений інтеграл.
- •7.1. Умови існування визначеного інтеграла.
- •7.1.1. Означення визначеного інтеграла.
- •7.1.2. Класи інтегрованих функцій.
- •7.2. Основні властивості визначеного інтеграла.
- •7.3. Основна формула інтегрального числення.
- •7.4. Основні правила інтегрування.
- •7.4.1. Заміна змінної у визначеному інтегралі.
- •7.4.2. Інтегрування частинами у визначеному інтегралі.
- •7.5. Методи наближеного обчислення.
- •7.6. Геометричне застосування визначеного інтеграла.
- •7.6.1. Площа плоскої фігури.
- •7.6.2. Об’єм тіла обертання та площі поверхні тіла обертання.
- •7.8. Деякі застосування в економіці.
- •7.8.1. Витрати, доход та прибуток.
- •7.8.2. Коефіцієнт нерівномірного розподілу прибуткового податку.
- •7.8.3. Максимізація прибутку за часом.
- •7.8.4. Стратегія розвитку.
- •Питання для самоконтролю.
- •Вправи до розділу “Невизначений інтеграл”.
- •Використовуючи правила інтегрування та таблицю основних інтегралів, знайти інтеграли:
- •Обчислити інтеграли методом підстановки.
- •Обчислити інтеграли методом інтегрування частинами.
- •Використовуючи піднесення під диференціал обчислити наступні інтеграли.
- •Використовуючи невизначений інтеграл, розв’язати задачі економічного змісту.
- •Правила виконання і оформлення контрольних завдань.
- •Індивідуальне контрольне завдання по темі “Невизначений інтеграл”.
- •Вправи до розділу “Визначені та невласні інтеграли”.
- •Обчислити інтеграли:
- •Знайти площу фігури, обмеженої заданими лініями:
- •Знайти об’єм тіла, утвореного обертанням навколо осі фігури, обмеженої слідуючими лініями:
- •Дослідити невласні інтеграли:
- •Індивідуальне контрольне завдання по темі “Визначені та невласні інтеграли”.
- •Рекомендована література.
7.6. Геометричне застосування визначеного інтеграла.
7.6.1. Площа плоскої фігури.
Якщо
на відрізку
![]() функція
функція
![]() ,
то згідно з формулою
,
то згідно з формулою
![]() ,
обчислення площі криволінійної трапеції,
зображеної на рис.1, можна знайти за
формулою
,
обчислення площі криволінійної трапеції,
зображеної на рис.1, можна знайти за
формулою
![]() .
.
Якщо
на відрізку
![]() функція
функція
![]() ,
то криволінійна трапеція, обмежена
кривою
,
то криволінійна трапеція, обмежена
кривою
![]() ,
відрізка
,
відрізка
![]() та прямими
та прямими
![]() і
і
![]() ,
буде розташована нижче осі
,
буде розташована нижче осі
![]() .
Визначений інтеграл
.
Визначений інтеграл
![]() у цьому випадку буде
у цьому випадку буде
![]() .
Але площа є невід’ємною величиною, тому
площу криволінійної трапеції, розташованої
нижче осі
.
Але площа є невід’ємною величиною, тому
площу криволінійної трапеції, розташованої
нижче осі
![]() ,
треба знаходити за формулою
,
треба знаходити за формулою
![]() або
або
![]() .
.
Я кщо
кщо
![]() на відрізку
на відрізку
![]() ,
декілька разів змінює знак, то інтеграл
по відрізку
,
декілька разів змінює знак, то інтеграл
по відрізку
![]() треба розбити на суму інтегралів по
часткових відрізках. Інтеграл буде
додатним на тих відрізках, де
треба розбити на суму інтегралів по
часткових відрізках. Інтеграл буде
додатним на тих відрізках, де
![]() та від’ємним
там, де
та від’ємним
там, де
![]() .
Інтеграл по відрізку
.
Інтеграл по відрізку
![]() дає різницю площ, що лежать вище та нижче
осі
дає різницю площ, що лежать вище та нижче
осі
![]() .
.
Щоб
одержати суму площ (без врахування
розташування відносно осі
![]() )
треба знайти суму абсолютних величин
інтегралів по часткових відрізках або
обчислити інтеграл від абсолютного
значення функції, тобто
)
треба знайти суму абсолютних величин
інтегралів по часткових відрізках або
обчислити інтеграл від абсолютного
значення функції, тобто
![]() .
.
Приклад:
Обчислити площу фігури обмеженої лініями
![]() та
та
![]() .
.
Розв’язування. Спочатку зобразимо фігуру, площу якої треба знайти.
З найдемо
точку перетину цих парабол. Координати
точок перетину задовольняють обом
рівнянням, тому
найдемо
точку перетину цих парабол. Координати
точок перетину задовольняють обом
рівнянням, тому
![]() .
Отже, площа заштрихованої фігури буде:
.
Отже, площа заштрихованої фігури буде:
![]() .
.
рис. 3.
7.6.2. Об’єм тіла обертання та площі поверхні тіла обертання.
Н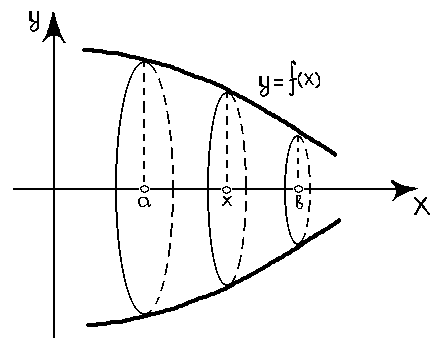 ехай
криволінійна трапеція, обмежена кривою
ехай
криволінійна трапеція, обмежена кривою
![]() ,
відрізком
,
відрізком
![]() осі
осі
![]() та прямими
та прямими
![]() та
та
![]() обертається навколо осі
обертається навколо осі
![]() (рис 3.). Тоді об’єм
тіла обертання можна знайти за формулою
(рис 3.). Тоді об’єм
тіла обертання можна знайти за формулою
![]() ,
а площу поверхні обертання за формулою
,
а площу поверхні обертання за формулою
![]() .
.
Приклад:
Обчислити об’єм
кулі радіуса
![]() .
.
Розв’язування.
Кулю можна розглядати як результат
обертання полукруга, обмеженого частиною
кола
![]() ,
навколо осі
,
навколо осі
![]() .
Використовуючи рівність
.
Використовуючи рівність
![]() ,
симетричність кола відносно осі
,
симетричність кола відносно осі
![]() та формулу
та формулу
![]() ,
одержимо
,
одержимо
![]() кулі:
кулі:
![]() .
.
7.7. Невласні інтеграли.
Згідно з теоремою існування визначеного інтеграла цей інтеграл існує, якщо виконані умови:
-
відрізок інтегрування
 скінчений;
скінчений; -
підінтегральна функція
 неперервна або обмежена і має скінчену
кількість точок розриву.
неперервна або обмежена і має скінчену
кількість точок розриву.
Якщо хоч одна з умов не виконується, то визначений інтеграл називають невласним.
Якщо
не виконується перша умова, то
![]() або
або
![]() або
або
![]() та
та
![]() ,
то інтеграли називають невласними
інтегралами з нескінченими межами.
,
то інтеграли називають невласними
інтегралами з нескінченими межами.
Якщо
не виконується лише друга умова, то
підінтегральна функція
![]() має точки розриву другого роду на
відрізку інтегрування
має точки розриву другого роду на
відрізку інтегрування
![]() .
В цьому випадку
.
В цьому випадку
![]() називають невласним інтегралом від
розривної функції або від функції,
необмеженої в точках відрізку інтегрування.
називають невласним інтегралом від
розривної функції або від функції,
необмеженої в точках відрізку інтегрування.
Дослідження невласних інтегралів.
Дослідження невласних інтегралів проводять шляхом використання граничного переходу до визначеного інтеграла.
Інтеграли з необмеженими межами розглядають так:
![]() .
.
![]() .
.
Якщо вказані границі існують (будуть скінченими числами), то відповідний інтеграл називають збіжним і він дорівнює своїй границі. Якщо якась границя не існує або дорівнює нескінченості, то інтеграл називають розбіжним.
Приклад:
Обчислити інтеграл
![]() або встановити його розбіжність.
або встановити його розбіжність.
Розв’язування: Згідно з означенням невласного інтеграла, маємо:
![]() .
Отже, цей інтеграл, збіжний і дорівнює
1.
.
Отже, цей інтеграл, збіжний і дорівнює
1.
У
випадку необмеженої на
![]() функції
функції
![]() її точки розриву можуть бути на лівому
кінці або на правому кінці або всередині
проміжку інтегрування
її точки розриву можуть бути на лівому
кінці або на правому кінці або всередині
проміжку інтегрування
![]() .
У цих випадках невласні інтеграли
визначають так:
.
У цих випадках невласні інтеграли
визначають так:
![]()
 Якщо
вказані границі існують, то відповідний
інтеграл називають збіжним. У протилежному
випадку розбіжним.
Якщо
вказані границі існують, то відповідний
інтеграл називають збіжним. У протилежному
випадку розбіжним.
Приклад:
Обчислити інтеграл
![]() або встановити розбіжність.
або встановити розбіжність.
Розв’язування:
В точці
![]() підінтегральна функція необмежена,
тобто вона має розрив всередині проміжка
інтегрування. За означенням такого
невласного інтеграла маємо:
підінтегральна функція необмежена,
тобто вона має розрив всередині проміжка
інтегрування. За означенням такого
невласного інтеграла маємо:

![]() .
Отже, інтеграл розбіжний.
.
Отже, інтеграл розбіжний.
