6.6.5. Інтегрування виразів, що містять ірраціональності.

Інтеграли від ірраціональних функцій можуть бути зведені за допомогою підстановок до інтегралів від раціональних функцій.

Розглянемо декілька прикладів.

1. Підінтегральна функція є раціональним дробом відносно , де - дробове число. У цьому випадку вводять нову змінну , де - спільний знаменник дробових показників степеня змінної .

Приклад: Знайти

Розв’язування: Маємо: . Спільний знаменник дробових показників змінної дорівнює . Тому зробимо підстановку , і одержимо:

2. Підінтегральний вираз містить дробові степені лінійного двочлена . У цьому випадку доцільно зробити підстановку , де - спільний знаменник дробових показників степенів двочлена.

Приклад: Знайти

Нехай ; тоді

Одержимо:

3. Інтеграли типу - зводяться до табличного, шляхом виділення повного квадрата з квадратного тричлена.

Приклад 1:

Приклад 2:

4. Інтеграли виду , зводяться до табличного шляхом виділення повного квадрата, або за допомогою формули .

Приклад 1:

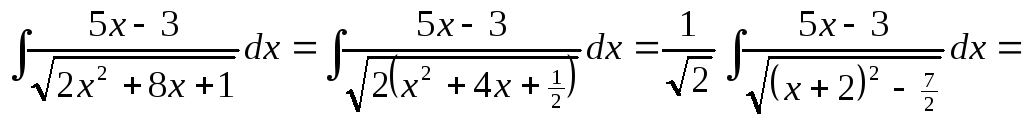
Другий спосіб:

5. Інтеграл виду , знаходяться за допомогою підстановки

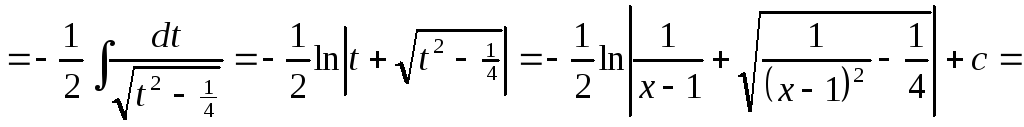
6. Інтеграл типу де , знаходяться за допомогою підстановок:

1. де - найменший спільний знаменник дробів і .

2. - ціле, - - знаменник дробу .

3. - ціле, - - знаменник дробу .

Приклад:

6.6.6. Інтегрування деяких тригонометричних виразів.

1. Невизначені інтеграли виду:

за допомогою тригонометричних формул ,

зводяться до інтегралів

Приклад:

2. Невизначені інтеграли виду: де і - натуральні числа, знаходяться за допомогою тригонометричних формул

якщо і -парні. Якщо хоча б одне з них і - непарне, то від непарного степеня відділяється множник і вводиться нова змінна. Якщо , то

тобто заміна , якщо , то . Останній інтеграл знаходиться безпосередньо (як інтеграл від алгебраїчного многочлена).

Приклад:

3. Невизначений інтеграл , де - раціональна функція від і , шляхом введення нової змінної за формулою зводиться до інтегралу , де - раціональна функція змінної .

Приклад: Знайти Використаємо підстановку , де

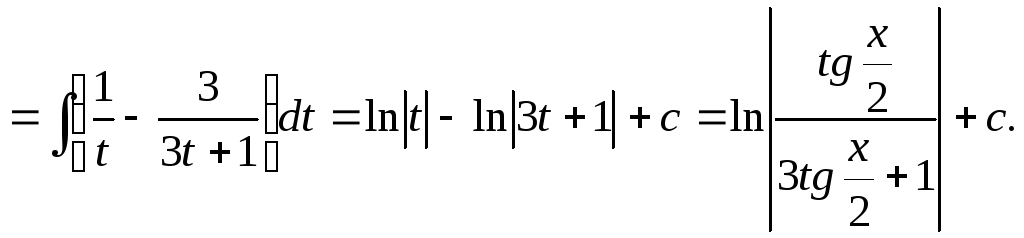
6.6.8. Раціональна функція від .

Інтеграл виду раціоналізується підстановкою , звідки .

Приклад: Знайти

Розділ 7. Визначений інтеграл.

7.1. Умови існування визначеного інтеграла.

7.1.1. Означення визначеного інтеграла.

7.1.2. Класи інтегрованих функцій.

7.2. Основні властивості визначеного інтеграла.

7.3. Основна формула інтегрального числення.

7.4. Основні правила інтегрування.

7.4.1. Заміна змінної у визначеному інтегралі.

7.4.2. Інтегрування частинами у визначеному інтегралі.

7.5. Методи наближеного обчислення.

7.6. Геометричне застосування визначеного інтеграла.

7.6.1. Площа плоскої фігури.

7.6.2. Об’єм тіла обертання.

7.7. Деякі застосування в економіці.

7.8. Невласні інтеграли.

7.1. Умови існування визначеного інтеграла.

7.1.1. Означення визначеного інтеграла.

Нехай функція задана на відрізку . Розіб’ємо відрізок на довільних частин точками: . Виберемо в кожному з частинних відрізків довільну точку : ; ; ;

Тепер утворимо суму добутків: , яку будемо називати інтегральною сумою для функцій на відрізку .

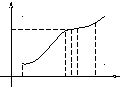
рис. 1.

Геометричний зміст велечини показаний на рис.1. це сума площ прямокутників з основою і висотою . Введемо ще одну велечину. Позначимо через довжину максимального частинного відрізка даного розбиття: .

Означення: Скінченна границя інтегральної суми при , якщо вона існує, незалежна від способу ділення відрізка на частини та добору точок , то ця границя називається визначеним інтегралом від функції на відрізку і позначається .

Математично це означення можна записати так: .

Якщо визначений інтеграл існує, то функція називається інтегрованою на відрізку , числа і - відповідно нижньою і верхньою межами, - підінтегральна функція, - змінна інтегрування.

Величина визначеного інтеграла, відповідно даному вище означенню, однозначно визначається видом функції і числами і . Визначений інтеграл не залежить від позначення змінної інтегрування, тобто: .