
- •Вступ Невизначений і визначений інтеграли.
- •Розділ 6. Невизначений інтеграл.
- •6.1. Первісна та її властивості.
- •6.2. Невизначений інтеграл і його властивості.
- •6.6. Основні методи інтегрування.
- •6.6.1. Метод безпосереднього інтегрування.
- •6.6.2. Метод підстановки (заміни змінної).
- •6.6.3. Метод інтегрування частинами.
- •Рекомендації до застосування методу інтегрування частинами.
- •6.6.4. Інтегрування раціональних дробів.
- •6.6.5. Інтегрування виразів, що містять ірраціональності.
- •6.6.6. Інтегрування деяких тригонометричних виразів.
- •6.6.8. Раціональна функція від .
- •Розділ 7. Визначений інтеграл.
- •7.1. Умови існування визначеного інтеграла.
- •7.1.1. Означення визначеного інтеграла.
- •7.1.2. Класи інтегрованих функцій.
- •7.2. Основні властивості визначеного інтеграла.
- •7.3. Основна формула інтегрального числення.
- •7.4. Основні правила інтегрування.
- •7.4.1. Заміна змінної у визначеному інтегралі.
- •7.4.2. Інтегрування частинами у визначеному інтегралі.
- •7.5. Методи наближеного обчислення.
- •7.6. Геометричне застосування визначеного інтеграла.
- •7.6.1. Площа плоскої фігури.
- •7.6.2. Об’єм тіла обертання та площі поверхні тіла обертання.
- •7.8. Деякі застосування в економіці.
- •7.8.1. Витрати, доход та прибуток.
- •7.8.2. Коефіцієнт нерівномірного розподілу прибуткового податку.
- •7.8.3. Максимізація прибутку за часом.
- •7.8.4. Стратегія розвитку.
- •Питання для самоконтролю.
- •Вправи до розділу “Невизначений інтеграл”.
- •Використовуючи правила інтегрування та таблицю основних інтегралів, знайти інтеграли:
- •Обчислити інтеграли методом підстановки.
- •Обчислити інтеграли методом інтегрування частинами.
- •Використовуючи піднесення під диференціал обчислити наступні інтеграли.
- •Використовуючи невизначений інтеграл, розв’язати задачі економічного змісту.
- •Правила виконання і оформлення контрольних завдань.
- •Індивідуальне контрольне завдання по темі “Невизначений інтеграл”.
- •Вправи до розділу “Визначені та невласні інтеграли”.
- •Обчислити інтеграли:
- •Знайти площу фігури, обмеженої заданими лініями:
- •Знайти об’єм тіла, утвореного обертанням навколо осі фігури, обмеженої слідуючими лініями:
- •Дослідити невласні інтеграли:
- •Індивідуальне контрольне завдання по темі “Визначені та невласні інтеграли”.
- •Рекомендована література.
6.6.2. Метод підстановки (заміни змінної).
Заміна змінної інтегрування являється одним з самих ефективних методів зведення невизначеного інтеграла до табличного. Він ґрунтується на слідуючій теоремі:
Теорема:
Нехай
функція
![]() визначена і диференційована на деякому
проміжку
визначена і диференційована на деякому
проміжку
![]() ,
а
,
а
![]() -
множина значень цієї функції, на якій
визначена функція
-
множина значень цієї функції, на якій
визначена функція
![]() .
Тоді якщо функція
.
Тоді якщо функція
![]() має первісну на множині
має первісну на множині
![]() ,
то на множині
,
то на множині
![]() справедлива формула
справедлива формула
![]() .
.
Цю формулу називають формулою заміни змінної в невизначеному інтегралі.
Розглянемо використання цього методу на прикладах обчислення інтегралів.
Приклад:
1)

Після
знаходження інтеграла потрібно
повернутись до змінної
![]() .
.
Зауваження:
-
Якщо підстановка обрана вдало, то одержаний інтеграл буде простішим і мета підстановки буде досягнута.
-
Якщо підінтегральний вираз містить корінь вигляду
 ,
то доцільно застосовувати тригонометричну
підстановку
,
то доцільно застосовувати тригонометричну
підстановку
 або
або
 .
.
Приклад:
Знайти інтеграл
![]()
Розв’язування:
Зробимо підстановку
![]() ,
тоді
,
тоді
![]() .
.
Одержимо:

Із
рівності
![]() ,
одержимо
,
одержимо
![]() .
.
Отже,
![]() .
.
6.6.3. Метод інтегрування частинами.
Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча б одна з них є трансцендентною (не степеневою).
Нехай
![]() та
та
![]() деякі функції
деякі функції
![]() ,
тобто
,
тобто
![]() ,
,
![]() .
Розглянемо диференціал добутку цих
функцій
.
Розглянемо диференціал добутку цих
функцій
![]() .
Інтегруючи обидві частини рівності,
одержимо
.
Інтегруючи обидві частини рівності,
одержимо
![]() .
Звідси, враховуючи властивість
невизначеного інтеграла, маємо
.
Звідси, враховуючи властивість
невизначеного інтеграла, маємо
![]() .
Отже, одержимо формулу
.
Отже, одержимо формулу
![]() ,
яку називають формулою інтегрування
частинами. Ця формула дозволяє знаходження
інтегралу виду
,
яку називають формулою інтегрування
частинами. Ця формула дозволяє знаходження
інтегралу виду
![]() .
При вдалому обранні
.
При вдалому обранні
![]() та
та
![]() інтеграл може бути табличним або
простішим ніж заданий інтеграл
інтеграл може бути табличним або
простішим ніж заданий інтеграл
![]() .
.
Приклад:
Знайти
![]() .
.
 .
.
Рекомендації до застосування методу інтегрування частинами.
При
обранні
![]() та
та
![]() слід пам’ятати,
що спрощення заданого інтеграла можливе
за рахунок диференціювання функції
слід пам’ятати,
що спрощення заданого інтеграла можливе
за рахунок диференціювання функції
![]() .
.
В інтегралах виду:
![]() доцільно
обирати
доцільно
обирати
![]() ,
а залишену частину підінтегрального
виразу позначити
,
а залишену частину підінтегрального
виразу позначити
![]() .
.
В
інтегралах виду:
![]() доцільно
доцільно
обирати
![]() ,
а залишок підінтегрального виразу за
,
а залишок підінтегрального виразу за
![]() .
.
В інтегралах:
![]() ,
можна приймати за
,
можна приймати за
 або
або
 .
.
Приклади: Знайти інтеграли:
-
 .
. -

 Одержимо
з утвореної рівності:
Одержимо
з утвореної рівності:

6.6.4. Інтегрування раціональних дробів.
Означення:
Дріб
називається раціональним, якщо його
чисельник і знаменник є многочлени,
тобто дріб має вигляд
 ,
де
,
де
![]() і
і
![]() -
коефіцієнти многочленів,
-
коефіцієнти многочленів,
![]() .
.
Раціональний
дріб називається правильним, якщо
![]() ,
і неправильним, якщо
,
і неправильним, якщо
![]() .
Якщо дріб
.
Якщо дріб
![]() неправильний, тоді потрібно поділити
чисельник на знаменник (за правилом
ділення многочленів) і одержати заданий
дріб у вигляді суми многочлена та
правильного дробу, тобто
неправильний, тоді потрібно поділити
чисельник на знаменник (за правилом
ділення многочленів) і одержати заданий
дріб у вигляді суми многочлена та
правильного дробу, тобто
![]() .
.
Означення: Найпростішими раціональними дробами називають правильні дроби вигляду:
Умова
![]() означає, що квадратний тричлен
означає, що квадратний тричлен
![]() не має дійсних коренів і на множники не
розкладається. Аналогічно з
не має дійсних коренів і на множники не
розкладається. Аналогічно з
![]() ,
де
,
де
![]() .
.
Розглянемо інтегрування найпростіших раціональних дробів на прикладах.
Перші два типи інтегралів знаходять методом безпосереднього інтегрування:
-
 .
. -

При інтегруванні найпростішого дробу 3-го типу спочатку потрібно виділити повний квадрат, а потім той вираз, що під квадратом, замінити через одну змінну.


![]()
Знаючи
формулу
![]() ,
даний інтеграл можна знаходити:
,
даний інтеграл можна знаходити:

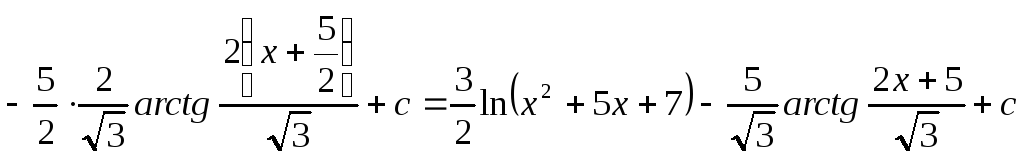 .
.
-
Інтеграл від найпростішого дробу 4-го типу шляхом повторного інтегрування частинами зводять до інтеграла від найпростішого дробу 3-го типу.
У повному курсі вищої алгебри доведена слідуючи теорема.
Теорема: Будь-який неправильний раціональний дріб розкладається на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів.
Отже,
інтегрування раціонального дробу
зводиться до інтегрування многочлена
![]() (при
(при
![]() )
та суми найпростіших дробів, що
визначаються коренями знаменника
)
та суми найпростіших дробів, що
визначаються коренями знаменника
![]() .
.
Можливі наступні випадки:
-
Корені знаменника дійсні і різні, тобто
 .
В цьому випадку дріб розкладається
.
В цьому випадку дріб розкладається
 на суму найпростіших дробів 1-го типу:
на суму найпростіших дробів 1-го типу:
![]() ,
з цієї тотожності знаходять невизначені
коефіцієнти
,
з цієї тотожності знаходять невизначені
коефіцієнти
![]() .
.
-
Корені знаменника дійсні, причому деякі з них кратні, тобто
 .
Тоді дріб
.
Тоді дріб
 розкладається на суму найпростіших
дробів 1-го і 2-го типу
розкладається на суму найпростіших
дробів 1-го і 2-го типу
 ,
з цієї тотожності визначаються
коефіцієнти
,
з цієї тотожності визначаються
коефіцієнти
 .
. -
Корені знаменника дійсні, причому деякі з них кратні, крім того знаменник містить квадратний тричлен, який не розкладається на множники, тобто
 .
В цьому випадку дріб
.
В цьому випадку дріб
 розкладається на суму найпростіших
дробів 1-го, 2-го, 3-го типів
розкладається на суму найпростіших
дробів 1-го, 2-го, 3-го типів
 ;
з цієї тотожності знаходять коефіцієнти
;
з цієї тотожності знаходять коефіцієнти
 та
та
 .
.
Приклад:
Знайти
![]()
Розв’язування:
Підінтегральна функція – це правильний
раціональний дріб, знаменник якого
містить квадратний двочлен, який не
розкладається на множники та один
дійсний корінь
![]() ,
тому цей дріб розкладається на суму
найпростіших дробів 1-го та 3-го типу:
,
тому цей дріб розкладається на суму
найпростіших дробів 1-го та 3-го типу:
![]()
Невідомі
коефіцієнти
![]() будемо шукати методом невизначених
коефіцієнтів. Для цього праву частину
рівності треба привести до спільного
знаменника, одержимо:
будемо шукати методом невизначених
коефіцієнтів. Для цього праву частину
рівності треба привести до спільного
знаменника, одержимо:
![]()
Знаменники
в обох частинах рівні, тому і чисельники
повинні бути рівні;
![]() ,
ця рівність можлива лише тоді, коли
коефіцієнти при однаковому степені
,
ця рівність можлива лише тоді, коли
коефіцієнти при однаковому степені
![]() в обох частинах рівності однакові,
тобто:
в обох частинах рівності однакові,
тобто:

Отже,
розклад прийме вигляд:

Інтегруючи цю рівність, одержимо:
![]()
![]()

