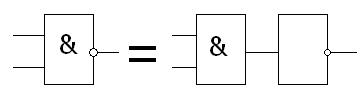Логические элементы

Логический элемент – это такая схема, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе

Название элемента	Инвертор	Конъюнктор	Дизъюнктор
Операция	Логическое отрицание	Логическое умножение	Логическое сложение
Обозначение на схеме

Используя логические элементы, можно составлять схемы:

Например: Определите:

Операция И - НЕ - инверсия функции конъюнкции (штрих Шеффера)	Операция ИЛИ - НЕ - инверсия функции дизъюнкции (стрелка Пирса)

Составить таблицу истинности для следующей схемы:

Правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

• "1" тогда и только тогда, когда хотя бы на одном входе действует «0»,

• "0" тогда и только тогда, когда на всех входах действуют «1»

Правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

• "1" тогда и только тогда, когда на всех входах действуют «0»,

• "0" тогда и только тогда, когда хотя бы на одном входе действует «1»

Законы логики

Самые важные из них:

ЗАКОН ПРОТИВОРЕЧИЯ	X 
ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО	X 
ЗАКОН ДВОЙНОГО ОТРИЦАНИЯ	= X
ЗАКОН ИДЕМПОТЕНТНОСТИ	X X = X		X X = X
ЗАКОН КОММУТАТИВНОСТИ (переместительности)	X Y = Y 		X Y = Y 
ЗАКОН АССОЦИАТИВНОСТИ (сочетательности)	             		              
ЗАКОН ДИСТРИБУТИВНОСТИ (распределительности)	                                    
ЗАКОНЫ ДЕ МОРГАНА	= 	= 
ЗАКОН ПОГЛОЩЕНИЯ	                 
ЗАКОН СКЛЕИВАНИЯ	                      
ЗАКОН ИСКЛЮЧЕНИЯ КОНСТАНТ	X 1 	    
	    	    

Используя законы логики упростить следующие выражения:

1. Преобразовать формулу A^ 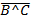так, чтобы в ней не использовались знаки логического умножения

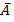
2. Преобразовать формулу ( Стак, чтобы в ней не использовались знаки логического сложения.

3. Упростить формулу (АВ)(АС)

4. Упростить формулу 

11