Сложение и умножение двоичных чисел Правила сложения двоичных чисел

Сложение производится как обычно, столбиком, поразрядно.

Рассмотрите следующие примеры:

Правила умножения двоичных чисел

Умножение производится как обычно, столбиком, поразрядно.

Рассмотрите следующие примеры:

Во множителе (2 число) значимая единица располагается на 5 позиции. В ответе к множимому (1 число) дописано 5 нулей, т.е. число сместили на 5 единиц влево, т.к.

В данном примере при записи промежуточных сумм записано только 3, пропущено умножение на 0, но следующие суммы все равно смещены влево. Иначе, ответ будет неверен.

При пропуске в записи промежуточных сумм не забывайте, соответствующая сумма записывается строго под разрядом, на который умножается множимое число.

Основы логики

Любое условие может иметь 2 значения:

ИСТИНА (TRUE) – обозначается 1 (или Т)

ЛОЖЬ (FALSE) – обозначается 0 (или F)

Для любой логической операции можно составить таблицу истинности, в которой записываются (как в таблице умножения) все возможные значения операндов и результаты операции.

Существуют 3 основные логические операции:

1. Логическое умножение (конъюнкция)

Обозначается разными способами: ^ AND & (на схемах)

Операция работает с 2 операндами (значениями).

Обратите внимание! Результат равен ИСТИНА, если оба операнда (высказывания) равны ИСТИНЕ.

Таблица истинности: По-другому это можно записать так:

или или

Примеры:

(5 > 4) ^ (4 < 8) = T ^ T = T

(1 ^ 0) ^ 1 = 1

(T ^ T) ^ F = F

2. Логическое сложение (дизъюнкция)

Обозначается разными способами: OR  1(на схемах)

Операция работает с 2 операндами (значениями).

Обратите внимание! Результат равен ИСТИНА, если хотя бы один из операндов равен ИСТИНЕ.

Таблица истинности: По-другому это можно записать так:

или

Примеры:

(5 > 4)  (4 < 3) = T  F = T

(0 0)  1 = 1

(F  T)  (T  T) = T

3. Логическое отрицание (инверсия)

Обозначается разными способами: NOT НЕ 

Операция работает с 1 операндом (значением).

Т

Обратите внимание! Значение операнда изменяется на противоположное (инвертируется).

аблица истинности: По-другому это можно записать так:

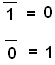
или

Примеры:

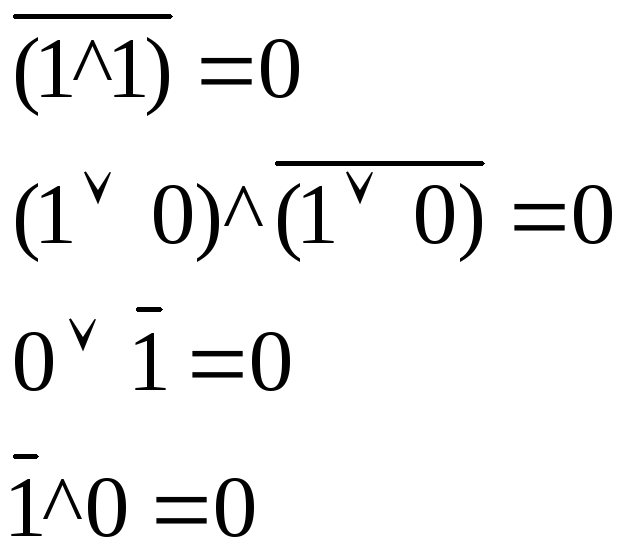
Существуют и другие логические операции, но они работают на основе этих трех. Например: И-НЕ, исключающее ИЛИ и т.д.

Элементы электроники и микросхемотехники

ЭЛЕКТРОНИКА – это наука о взаимодействии заряженных частиц (электронов, ионов) с электромагнитными полями и о методах создания электронных приборов и устройств (вакуумных, газоразрядных, полупроводниковых), используемых в основном для передачи, обработки и хранения информации.

Цифровая технология работает, в отличие от аналоговой, с дискретными, а не непрерывными сигналами. Кроме того, сигналы имеют небольшой набор значений, как правило, два. Обычно это 0 и 1, которые в булевской алгебре имеют значение: ИСТИНА и ЛОЖЬ.

Цифровые технологии главным образом используются в вычислительной цифровой электронике, прежде всего компьютерах, в различных областях электротехники, таких как игровые автоматы, робототехника, автоматизация, измерительные приборы, радио- и телекоммуникационные устройства и т. д.

Цифровые схемы состоят в основном из логических элементов, таких как AND, OR, NOT и др., а также могут быть связаны между собой счетчиками и триггерами. Современная цифровая интегральная микросхема - это миниатюрный электронный блок, содержащий в своем корпусе транзисторы, диоды, резисторы и другие активные и пассивные элементы, общее число которых может достигать нескольких десятков и даже сотен тысяч!

Булева алгебра - раздел математической логики, изучающий высказывания и операции над ними. Наиболее известными операциями булевой алгебры являются: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание.