Перевод числа из двоичной, восьмеричной, шестнадцатеричной систем в десятичную систему счисления

Для этого сначала необходимо для каждой цифры числа определить значение позиции: над цифрами проставляется номер позиции справа налево, начиная с нуля.

 Задание 4: Перевести число из двоичной системы счисления в десятичную: 11001₂ → X₁₀

Выполнение задания:

1. Для разрядов указать их позицию:

2. Результат вычисляется по формуле:

где n – количество разрядов в числе; i - номер позиции; 2 – заданное основание системы; цифра - цифра из исходного числа.

То есть для нашего примера получим:

При умножении на нуль результат равен нулю, поэтому разряды равные нулю можно не учитывать, т.е:

3. При переводе важно помнить значения степеней цифры 2.

20 =	1
21 =	2
22 =	4
23 =	8
24 =	16
25 =	32
26 =	64
27 =	128
28 =	256
29 =	512
210 =	1024

Для нашего примера получим:

Можете проверить результат задания 1: 11001₂ → 25₁₀

При переводе чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную, следует знать значения степеней с основанием 8 и 16.

80 = 1	160 = 1
81 = 8	161 = 16
82 = 64	162 = 256
83 = 512	163 = 4096
84 = 4096	164 = 65536
85 = 32768	165 = 1048576
86 = 262144	166 = 16777216
87 = 2097152	167 = 268435456
88 = 16777216	168 = 4294967296

 Задание 5: Перевести число из восьмеричной системы счисления в десятичную: 10000₈ → X₁₀

Выполнение задания:

Выполняется такое задание аналогично предыдущему, только следует не забывать, что заданная система счисления восьмеричная, следовательно, умножение разряда производится не на 2, а на 8.

, т.е. 10000₈ → 4096₁₀

Не забывайте, что в шестнадцатеричной системе счисления для кодирования используются 16 цифр: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F, где A=10, B=11, C=12, D=13, E=14, F=15

 Задание 6: Перевести число из шестнадцатеричной системы счисления в десятичную: 10001₁₆ → X₁₀

Выполнение задания:

Не забывайте, что заданная система счисления шестнадцатеричная, следовательно, умножение разряда производится не на 2, не на 8, а на 16.

,

т.е. 10001₁₆ → 65537₁₀

 Задание 7: Перевести число из восьмеричной системы счисления в шестнадцатеричную: 1101₈ → X₁₆

Выполнение задания:

т.е. результат: 1101₈ → 249₁₆

 Задание 8: Перевести число из двоичную системы счисления в шестнадцатеричную: 101100011₂ → X₁₆

Выполнение задания:

1. Исходное число нужно разбить на тетрады – 4 разряда, начиная справа, т.е.

2. Если число не разбивается ровно на тетрады (как в нашем примере), к оставшимся цифрам слева (в нашем примере, это 1) дописывается столько нулей, сколько не хватает до тетрады, т.е. «создается» искусственная тетрада.

3. Каждую тетраду необходимо заменить на соответствующее число в двоичной системе счисления, т.е. 0001 = 1, 0110 = 6, 0011 = 3. В переводе поможет таблица переводов со стр.8.

4. В результате записываются полученные значения в том же порядке:

т.е. результат: 101100011₂ → 163_16.

Можно проверить перевод, используя дополнительно десятичную систему счисления.

 Задание 9: Перевести число из шестнадцатеричной системы счисления в двоичную: 1B01₁₆ → X₂

Выполнение задания:

1. Каждый разряд исходного числа необходимо записать в виде тетрады – 4 разряда, т.е. 1 = 0001, B = 1011, 0 = 0000, 1 = 0001. В переводе поможет таблица переводов со стр.8.

2. В результате записать полученные тетрады в том же порядке:

1B01₁₆ → 0001 1011 0000 0001₂

Нули, стоящие на первых разрядах при записи можно опустить, так как они никак не повлияют на значение числа.

Результат: 1B01₁₆ → 1101100000001₂

 Задание 10: Перевести число из восьмеричной системы счисления в двоичную: 321₈ → X₂

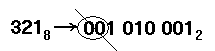
При переводах Х8 → X2 и Х2 → X8 используются триады (3 разряда).

 Задание 10: Перевести число из двоичной системы счисления в восьмеричную: 11011001₂ → X₈