3.5 Розгортні та нерозгортні поверхні

3.5.1 Лінійчасті розгортні поверхні

Криві поверхні утворюються за тими ж закономірно-стями, що і многогранні поверхні за умови, що нерухомою напрямною є крива лінія, а твірною може бути пряма або крива лінія, яка і характеризує дану поверхню. Розглянемо найпростіші з них.

Відкрита конічна поверхня утворюється прямою (твірною) лінією l, яка ковзає по відкритій кривій напрямній m і проходить через вершину S (рис. 3.9), проходячи послідовно через точки кривої А, В та С з положеннями l₁, l_{2 ,} l₃,... Сукупність цих положень твірної l утворює конічну поверхню. В перетині з площиною конічна поверхня утворює свій слід.

Відкрита циліндрична поверхня утворюється твірною l, яка переміщується по відкритій кривій m, зберігаючи паралельність твірної у кожному наступному положенні до попереднього (рис.3.10)

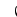
Рисунок 3.9 Рисунок 3.10

Відкрита циліндрична поверхня утворюється рухом твірної лінії l по відкритій твірній напрямній m паралельно до заданого напрямку n, послідовно проходячи через точки А, В, С (рис. 3.10).

Сукупність послідовних положень l, l₁, l₂ утворюють циліндричну поверхню. Аналогічні міркування справедливі для закритих конічних та циліндричних поверхонь. На рис 3.11 зображено проекції прямого кругового (а) та похилого (б) еліптичного конусів, прямого (в) та похилого еліптичного (г) циліндрів.

Рисунок 3.11

Для класифікації поверхонь використовують геометричну та алгоритмічну частину визначника. Геометричною частиною визначника є форма твірної, алгоритмічною – закон руху твірної. Отже, для лінійчастих поверхонь геометричною частиною визначника є пряма твірна лінія, алгоритмічною є крива напрямна. Через обмеженість об’єму лекцій інших розгортних поверхонь розглядати не будемо.

3.5.2 Лінійчасті нерозгортні поверхні

Лінійчасті нерозгортні поверхні на комплексному кресленні визначаються заданням трьох напрямних. При цьому можливі такі випадки:

а) усі напрямні – прямі лінії: утворюється лінійчастий однопорожнинний гіперболоїд;

б) одна з напрямних розміщена у нескінченості: утворюється гіперболічний параболоїд;

в) дві напрямні – мимобіжні прямі та площина паралелізму: утворюється поверхня у вигляді скісної площини (рис 3.12). Твірна l здійснює переміщення по мимобіжних напрямних а та b паралельно до горизонтально-проектуючої площини паралелізму Ф зі слідом Ф₁;

Рисунок 3.12

г ) дві напрямні – мимобіжні прямі та фронтальна площина паралелізму: утворюється поверхня гіперболічного параболоїда.

д) дві напрямні – прямі лінії, третя – крива лінія: утворюється поверхня – коноїд.

е) дві напрямні – криві лінії, одна пряма лінія: утворена поверхня – циліндроїд.

Поверхні за пунктами а, б, г, д, е на рисунку не показані (для ознайомлення з характером їх утворення див. додаткову рекомендовану літературу).

На рис.3.13 представлено поверхню коноїда, утвореного прямою напрямною а, кривою напрямною b, а третю напрямну замінено фронтальною площиною паралелізму Г₁, паралельно до якої проведені твірні l. Якщо прямолонійна напрямна а перпендикулярна до площини паралелізму, то коноїд називається прямим.

Якщо обидві напрямні – криві лінії , а одна (площина паралелізму) прямолінійна, то утворена крива поверхня називається циліндроїдом.

Якщо одна з криволінійних напрямних належить площині, перпендикулярній до площини паралелізму, то такий циліндроїд називається прямим.

Рисунок 3.13