2.7. Методы теплообмена излучением Закон Ламберта

Закон Стефана-Больцмана даёт значение количества энергии, излучаемой телом по всем направлениям полупространства. Энергию излучений, испускаемую по отдельным направлениям, можно вычислить по закону Ламберта.

Согласно закону Ламберта, поток излучения АЧТ в данном направлении пропорционален потоку излучения по нормали к поверхности и косинусу угла между ними.

, (18.1)

где – угловая плотность потока излучения.

Известно, что – яркость, интенсивность излучения.

. (18.2)

Из (18.2) следует, что яркость излучения одинакова по всем направлениям.

(здесь ср – стерадиан).

Рис. 18.1. Излучение элементарной площадки

Элементарная плотность потока излучения в направлении φ:

; (18.3)

; (18.4)

; (18.5)

. (18.6)

Можно доказать, что:

. (18.7)

Подставив (18.7) в (18.6), получаем:

. (18.8)

Подставим (8.11) в (18.8):

. (18.9)

Уравнение (18.9) служит основой для расчета лучистого теплообмена между поверхностями конечных размеров. Закон Ламберта строго справедлив для АЧТ. Для шероховатых тел опытом установлена его справедливость для φ в диапазоне от 0 до 60°, но при этом (по нормали). Для полированных металлов .

Теплообмен излучением между телами, произвольно расположенными в пространстве. Угловые коэффициенты

Получена расчётная зависимость для простейшего случая лучистого теплообмена – это приближенное значение для технических задач.

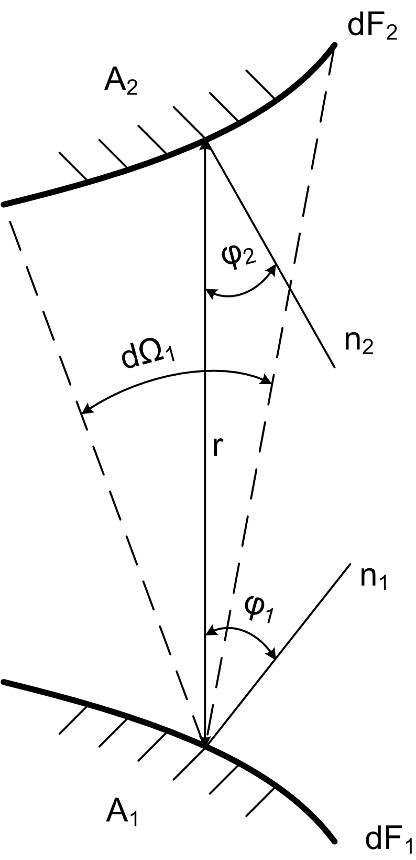
Рис. 18.2. Теплообмен излучением между двумя телами

Рассмотрим два произвольно расположенных тела с площадями dF₁ и dF₂. Температуры тел – Т₁, Т₂ (Т₁>Т₂); поглотительные способности – А₁, А₂; плотности потоков излучения – е₁, е₂.

; (18.10)

; (18.11)

. (18.12)

Величина – это телесный угол из точки А, под которым видна поверхность dF₂, а , – соответственно, наоборот.

; (18.13)

. (18.14)

Поскольку большинство технических материалов имеют достаточно высокий коэффициент поглощения , то можно ограничиться учётом лишь первого поглощения.

Количество энергии, полученное первым телом от второго:

; (18.15)

; (18.16)

; (18.17)

; (18.18)

; (18.19)

; (18.20)

; (18.21)

; (18.22)

, (18.23)

где Н_1,2 – взаимная поверхность лучистого теплообмена, она является чисто геометрическим параметром, который определяется размерами и формой поверхности тел, их взаимным расположением и расстоянием между ними.

, (18.24)

где – локальный и средний угловые коэффициенты облучённости.

Величина численно показывает, какая доля энергии, излучаемая dF₁ по всему полупространству, попадает на dF₂, а – усреднённое значение по F₂. Для некоторых технически важных случаев значения и есть в [2].

Лекция 19

Экраны

Для интенсификации лучистого теплообмена необходимо увеличить степень черноты поверхности, температуру Т₁ или обе эти величины вместе.

Рис. 19.1. Экран

Ранее получено:

. (19.1)

Процесс стационарный, между телами установлен экран. Тогда:

; (19.2)

. (19.3)

Из условия равенства плотностей потоков излучения получаем:

; (19.4)

. (19.5)

Подставим (19.5) в (19.2):

; (19.6)

; (19.7)

. (19.8)

В общем случае при для нескольких экранов имеем:

; (19.9)

. (19.10)

Если , то:

. (19.11)

Так, например, при , , получаем .