Метод размерностей. Π-теорема

Методами теории подобия можно получить безразмерные соотношения при наличии дифференциальных уравнений, описывающих процесс. Если их нет, но есть полный список размерных величин, существенных для рассматриваемого физического явления, безразмерные соотношения можно получить методом анализа размерностей.

Список размерных величин составляется интуитивно из физики процесса. Различают физические величины основные (первичные) и производные (вторичные).

В системе СИ (Système International) – основные единицы: длина, масса, время, абсолютная температура, сила тока, сила света, количества вещества и т.д.

Размерность – символическое выражение производной величины через основные (первичные).

В основе метода размерностей лежит теорема Фурье, согласно которой производную величину можно представить в виде:

, (17.1)

где С – коэффициент пропорциональности;

k – число основных единиц измерения в системе;

A_n – основная единица измерения;

i_n – характеристика производной единицы относительно основной.

«Выход» можно записать как произведение:

. (17.2)

Рассмотрим как пример турбулентный режим нестационарного процесса теплообмена при вынужденном движении. В этом случае:

. (17.3)

Представим (17.3) в виде (17.2):

, (17.4)

. (17.5)

Далее запишем единицы измерения для каждой величины, входящей в (17.5):

• ;

• ;

• ;

• ;

• ;

• ;

• ;

• .

Анализ показывает, что используются 4 основные единицы – кг, с, м, К. С учётом этого по (17.5) составляем систему уравнений:

(17.6)

Поскольку неизвестных 7, а уравнений 4, задаем значения 3 неизвестных: , , . Выразим остальные неизвестные через эти значения:

Для К:

. (17.7)

Для кг:

. (17.8)

Для с:

; (17.9)

; (17.10)

. (17.11)

Для м:

; (17.12)

; (17.13)

. (17.14)

Подставим (17.7), (17.8), (17.11), (17.14) в (17.4):

. (17.15)

Далее сгруппируем множители с одинаковым показателем степени:

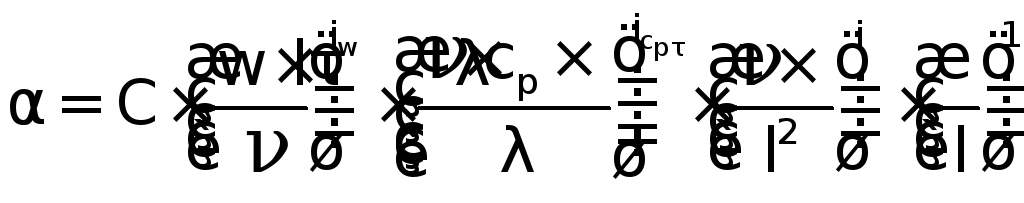; (17.16)

. (17.17)

Отдельно рассмотрим и :

; (17.18)

. (17.19)

Окончательно получаем:

. (17.20)

Таким образом, при нестационарной теплоотдаче .

Метод анализа размерностей как и теория подобия позволяет привести зависимость α от размерных величин к зависимости от чисел подобия. В примере число независимых величин уменьшилось с 7 до 3.

Результаты использования теории размерностей для получения обобщённых переменных подчиняются объему правилу – π-теореме:

Всякое соотношение между n размерными величинами, для измерения которых использовано k основных единиц измерения, можно представить в виде соотношения безразмерных комбинаций:

, ,…,.

В рассмотренном примере (включая α), , в итоге получено числа подобия – Nu, Re, Fo, Pr.

Эта теорема предназначена для контроля правильности приведения математической формулировки задачи к безразмерному виду.

2.6. Теплогидравлический расчёт теплообменных аппаратов

При заданной теплопроизводительности с увеличением скорости движения теплоносителей возрастает коэффициент теплоотдачи k и аппарат – более компактный:

. (17.21)

С другой стороны увеличиваются потери на трение:

. (17.22)

При проектировании ТОА необходимо решать совместно задачи теплообмена и гидравлического сопротивления и найти оптимальные характеристики.

Задача гидравлического расчёта – определение потерь давления при прохождении теплоносителей через аппарат.

Потери давления в общем случае:

. (17.23)

В теории теплообмена принято обозначать .

. (17.24)

Формула (17.24) справедлива для безотрывного течения.

Даже в самых простых аппаратах структура потока сложна, поэтому гидравлическое сопротивление рассчитывается приближенно:

. (17.25)

где – суммарные потери от трения на всех участках;

– местные потери;

– потери от ускорения потока вследствие неизотермичности течения (изменение объёма теплоносителя при постоянном сечении канала);

– сопротивление самотяги – вынужденному движению нагреваемой жидкости на нисходящем участке противодействует подъёмная сила, направленная вверх.

На практике Δp_у имеет значение при движении газов.

При вязком неизотермическом течении:

; (17.26)

. (17.27)

Для турбулентного и переходного режимов считаем по формуле (17.27).

, (17.28)

где – коэффициент местного сопротивления, зависит от характера препятствий, [1, 11].

При поперечном омывании пучков труб сопротивление трения мало по сравнению с сопротивлением формы (местные сопротивления).

Лекция 18