Теория подобия

Подобие может быть распространено на любые физические явления.

Физическое подобие наряду с постоянством соотношения длин, включает такое же постоянство соотношений между другими параметрами процесса, существенными для этого процесса.

Теория подобия позволяет:

• объединять размерные величины в безразмерные комплексы – это обобщённые переменные;

• сокращать число переменных под знаком функции;

• устанавливать условия переноса результатов лабораторных экспериментов на другие объекты.

Таким образом, теория подобия позволяет из анализа дифференциальных уравнений и условий однозначности сделать ряд выводов, не прибегая к интегрированию. Она дает теоретическую базу для постановки опытов и обработки экспериментальных данных, лежит в основе моделирования и широко используется в технике.

Лекция 6

Методы приведения к безразмерному виду Простейший метод – метод «губки»

, (6.1)

, (6.2)

. (6.3)

Число подобия Нуссельта Nu связывает интенсивность теплоотдачи с температурным полем в пограничном слое.

Числа теплового подобия при стационарном процессе – Nu, Gr, Pr.

, (6.4)

где g – ускорение свободного падения;

l – определяющий размер;

– кинематическая вязкость;

β – коэффициент объёмного расширения, ;

Δt – разность между температурой поверхности и омывающей жидкости.

Число подобия Грасгофа Gr характеризует подъёмную силу.

, (6.5)

где a – коэффициент температуропроводности.

Число подобия Прандтля Рr – мера подобия скоростных и температурных полей.

Числа гидродинамического подобия при стационарном процессе – Eu, Re.

, (6.6)

где Δp – разность давлений.

Число подобия Эйлера Еu – мера отношения сил давления к силам инерции в потоке.

. (6.7)

Число подобия Рейнольдса Re – мера отношения сил инерции к силам молекулярного трения.

Числа подобия бывают определяемые и определяющие.

Nu – это определяемое число (там есть α – искомая величина).

; (6.8)

. (6.9)

Уравнение (6.8) применяют при свободной конвекции, а (6.9) – при вынужденной.

Eu – это также определяемое число (в гидродинамике рассчитывают разность давлений ).

. (6.10)

Определяющие числа подобия составлены из величин, входящих в условия однозначности.

Получение эмпирических уравнений подобия

Когда дифференциальное уравнение и условия однозначности приведены к безразмерному виду и установлена функциональная связь между ними, количественную связь получают путём обработки экспериментальных данных.

Для примера рассмотрим стационарный процесс теплоотдачи от движущейся при турбулентном режиме жидкости в трубе:

. (6.11)

По данным измерений подсчитывают значения Re, Pr и соответствующие им значения Nu. Часто зависимость между числами подобия представляют в виде степенных функций, например:

, (6.12)

где постоянная C и показатели m и n являются постоянными безразмерными числами.

Для обработки опытных данных используются ЭВМ. Основываясь на математической статистике, постоянные C, m и n можно найти расчётным путём. Существуют специальные стандартные программы расчёта на ЭВМ, облегчающие работу.

Для наглядности рассмотрим получение расчётной зависимости путём её графического изображения в логарифмических координатах.

Прологарифмировав (6.12), получаем:

. (6.13)

Приняв Pr в качестве параметра, на график в координатах ― наносят подсчитанные значения Nu, Re, Pr. Если принятая степенная зависимость (6.12) верная, то получают семейство прямых¹.

Рис. 6.1. К определению показателя m

По одной из прямых находят показатель при числе Рейнольдса:

φ₁. (6.14)

Затем опытные данные наносят на график в координатах ―.

Рис. 6.2. К определению показателя n

Определяют показатель при числе Прандтля:

φ₂. (6.15)

Постоянную С находят из уравнения:

. (6.16)

При обобщении результатов опыта в числа подобия подставляют характерный размер – определяющий размер. Он входит в условия однозначности. Если течение в трубе, то определяющим будет внутренний диаметр. Если поток обтекает трубу с внешней стороны, определяющий – наружный диаметр.

Физические свойства, используемые в числах подобия, вычисляют при определяющей температуре. Как правило, это средняя температура жидкости.

Поэтому, при выборе уравнения подобия для теплового расчёта необходимо учитывать условия, при которых проведены эксперименты.

Основные используемые в инженерной практике выражения для Nu сведены в табл. 2.

Таблица 2

Уравнения подобия для расчёта среднего безразмерного коэффициента теплоотдачи

Вид поверхности нагрева и характеристика обтекания	Режим	Расчётные зависимости	Примечание
1	2	3	4
1. Теплоотдача при свободном движении (свободной конвекции)
1.1. В неограниченном пространстве			c n 1,18 0,54 0,135 , , – средняя температура потока и стенки; lo – наружный диаметр горизонтального трубопровода, шара, высота вертикального трубопровода, пластины.
1.2. В ограниченном пространстве		; ;	Рассчитывают теплообмен, эквивалентный теплопроводности: ; – коэффициент конвекции; . В узких длинных конструкциях возникает несколько циркуляционных контуров.
2. Теплоотдача при вынужденном движении (вынужденной конвекции)
2.1. Поток в трубе нагревание охлаждение	2.1.1. Вязкостный (ламинарный)		; ; , [2].
	2.1.2. Вязкостно-гравитационный (ламинарный)		– поправка на переменность физических свойств капельной жидкости. При вводят поправку ; для изогнутых труб , где R – радиус гиба.
1	2	3	4
	2.1.3. Турбулентный		1 10 20 30 50 1,90 1,28 1,13 1,05 1,00 – поправка на нестабильность на начальном участке. Определяющий размер для трубки – внутренний диаметр, а для каналов произвольного сечения: , f – площадь проходного сечения; u – смоченный периметр.
	2.1.4. Переходный
		2,2 2,3 2,5 3,0 3,5 4 5 6 7 8 9 10 2,2 3,6 4,9 7,5 10 12,2 16,5 20 24 27 30 33
Поток в кольцевом пространстве труб	2.1.5. Турбулентный		– внешний и внутренний диаметр кольца.
2.2. Поперечное омывание трубы	2.2.1. Капельной жидкостью		Re c m n 0,5 0,5 0,38 0,25 0,6 0,38 0,023 0,8 0,37
	2.2.2. Воздухом (*) (**)	(*) (**)	Определяющий размер – dн. Критерий Re – по скорости невозмущённого потока.
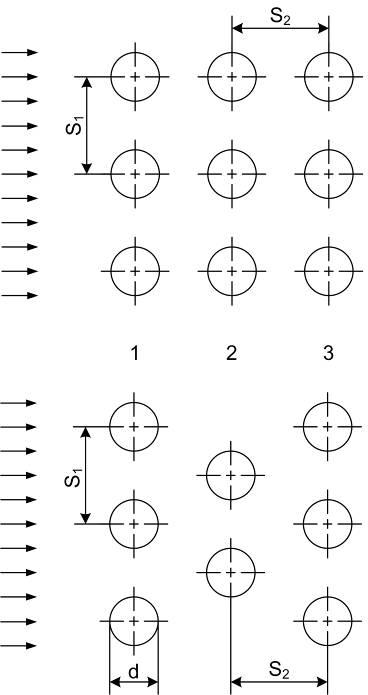
2.3. Поперечное омывание пучков (коридорных и шахматных)	2.3.1. Смешанный (*)	Для 3-го и всех последующих рядов: (*) (**) Для 1-го ряда , для 2-го ряда в коридорных пучках , в шахматных – .	εs – поправочный коэффициент, учитывающий влияние относительных шагов. Пучки с m n εs коридор- ные 0,26 0,65 0,33 шахмат- ные 0,41 0,6 0,33 при ; 1,12 при
	2.3.2. Турбулентный (**)
1	2	3	4
	(***) (коридорное) (****) (шахматное)	(***) (****)	При , ψ – угол атаки. Определяющий размер – наружный диаметр трубок dн, критерий Re – по скорости в самом узком поперечном сечении ряда. Определяющая температура – средняя температура жидкости . S1 – расстояние между осями труб поперек потока; S2 – расстояние между осями труб вдоль потока; α3 – коэффициент теплоотдачи для третьего и последующих рядов; αi – коэффициент теплоотдачи i-того ряда; n – число рядов в пучке; Fi – суммарная поверхность теплообмена трубок i-того ряда.

Лекция 7