11.3. Уравнение плоской волны, распространяющейся

в произвольном направлении

Найдем уравнение плоской волны, распространяющейся в произвольном направлении. Пусть данное направление составляет с осями координат x, y, z углы α, β и γ. Пусть колебания в плоскости, проходящей через начало координат, имеют вид

.

Рассмотрим волновую поверхность, удаленную на расстояние l от начала координат (рис. 11.3). Колебания в этой плоскости отстают на время :

.

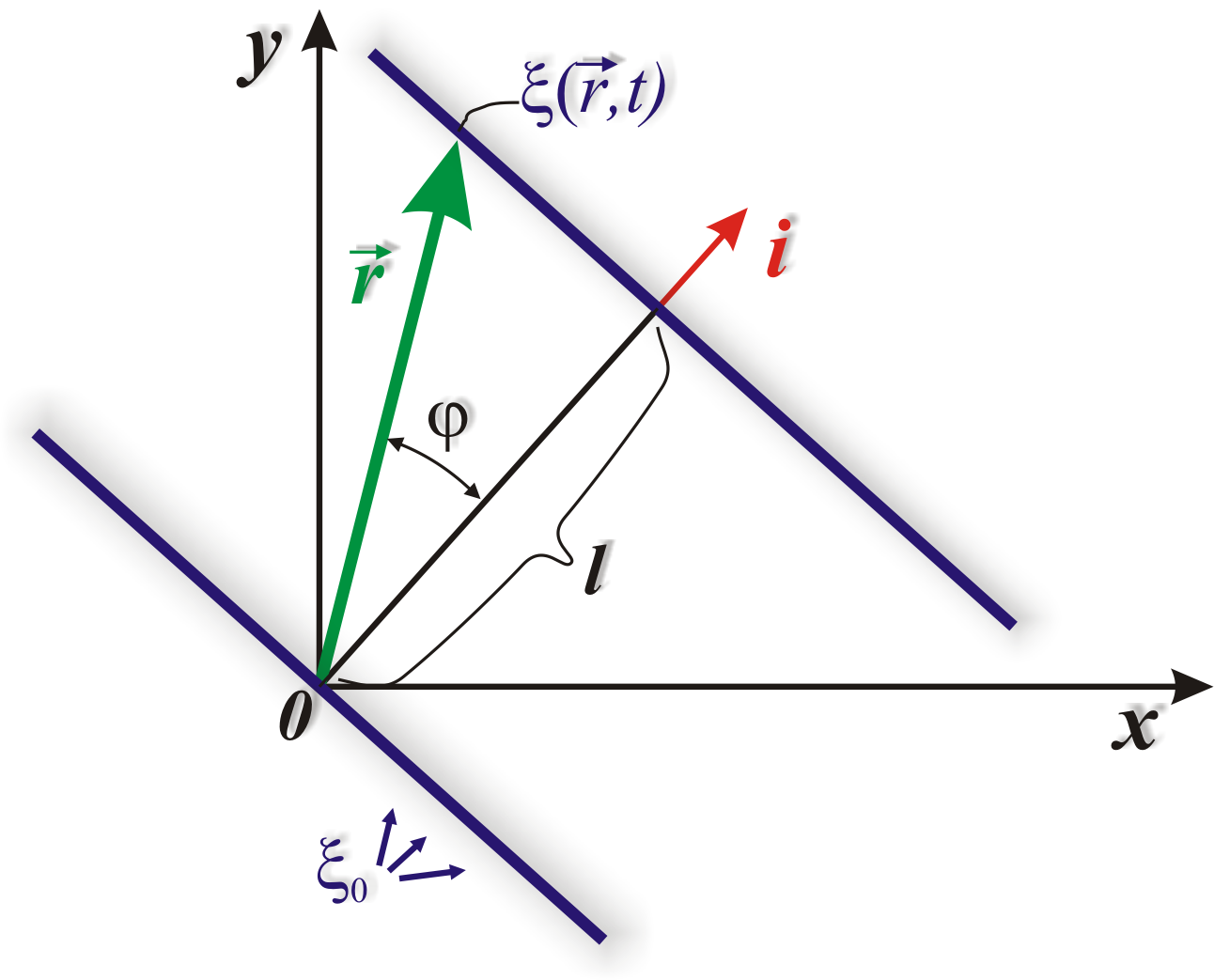
Рис. 11.3. Волновые поверхности плоской волны

Выразим l через радиус-вектор точек рассматриваемой поверхности. Пусть единичный вектор нормали к волновой поверхности. Скалярное произведение на радиус-вектор любой из точек поверхности имеет одно и то же значение, равное l:

.

Отсюда:

.

Вектор , равный по модулю волновому числу и направленный по нормали к поверхности называется волновым вектором. Учитывая это, получаем:

.

От радиуса-вектора точки можно перейти к ее координатам x, y, z:

; ,

где , , .

11.4. Волновое уравнение

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Найдем его вид. Запишем вторые производные по времени и координатам от функции, описывающей плоскую волну:

(11.3)

(11.4)

(11.5)

. (11.6)

Сложим правые и левые части уравнений (11.4) – (11.6):

.

Сопоставим полученное выражение с уравнением (11.3):

.

Учитывая, что , получаем:

. (11.7)

Полученное выражение и является искомым волновым урав-нением.

11.5. Скорость распространения упругих волн

Найдем скорость волны в тонком стержне. Тонким назовем стержень, толщина которого мала по сравнению с длиной волны. При малых продольных деформациях стержня справедлив закон Гука:

,

где σ – напряжение (Н/м²),

Е – модуль Юнга (Па),

.

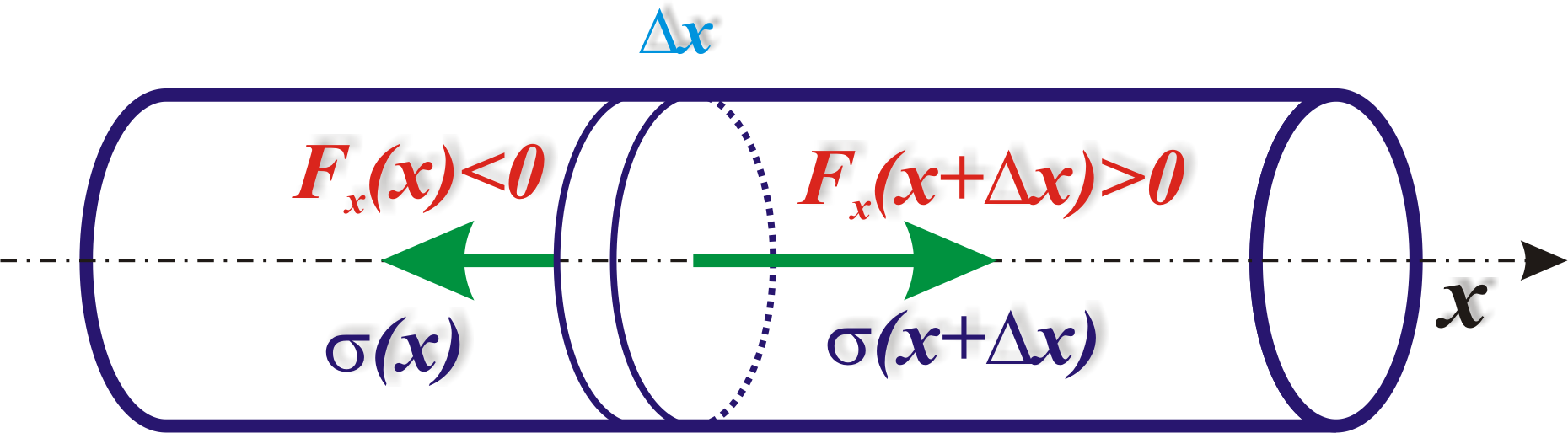
Рис. 11.4. Скорость волны в тонком стержне

Рассмотрим малый элемент стержня в момент, когда при прохождении волны он оказался в растянутом состоянии. Применим к этому элементу второй закон Ньютона:

,

где ρ – плотность материала стержня,

S – площадь его поперечного сечения. Правую часть уравнения можно переписать так:

,

где учтено, что слева F_x и σ имеют разные знаки. Тогда уравнение движения после сокращения на примет вид . Учтем закон Гука:

.

Получили волновое уравнение. В стержне будет распространяться продольная волна, скорость которой определим, сопоставив полученное выражение с (11.7):

.

Можно показать, что скорость поперечных упругих волн в неограниченной изотропной твердой среде

,

где G – модуль сдвига среды.