10.2. Решение дифференциального уравнения вынужденных

колебаний с помощью векторной диаграммы

Получим частное решение уравнения (10.1) с помощью векторной диаграммы. Предположим, что частное решение (10.1) имеет вид

х=аСоs(ωt-). (10.10)

Тогда

, (10.11)

. (10.12)

Подстановка выражений (10.10) – (10.12) в уравнение (10.1) приводит к соотношению

. (10.13)

а) б)

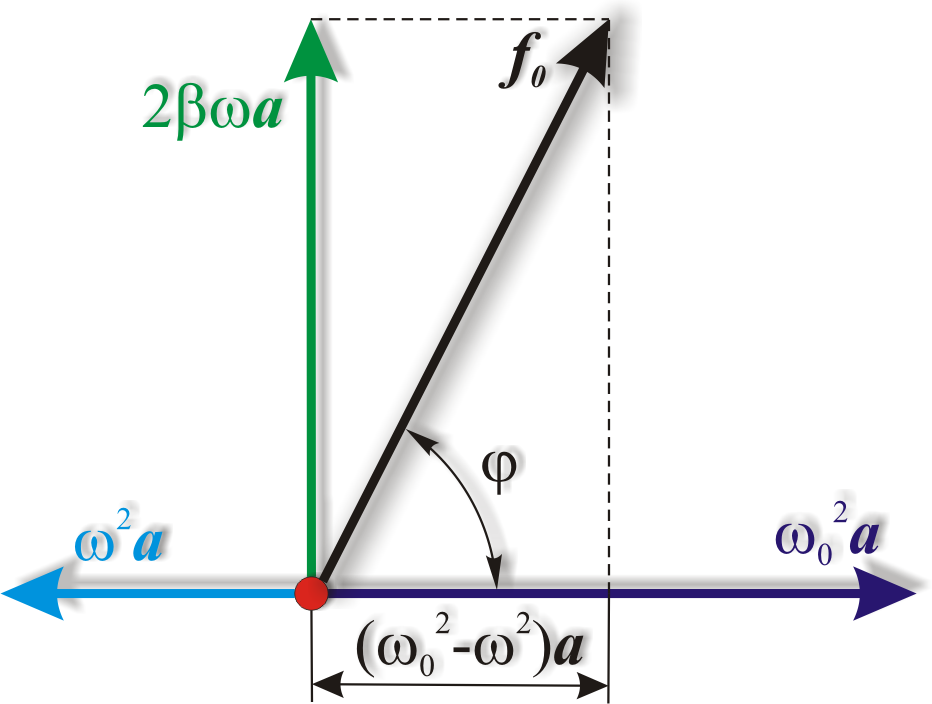
Рис. 10.1. Сложение амплитуд колебаний с помощью векторной диаграммы:

а- для случая   ω_0, б- для случая ω  ₀

Из (10.13) следует, что постоянные а и  должны иметь такие значения, чтобы гармоническая функция f₀Cosωt, была равна сумме трех гармонических функций, стоящих в левой части уравнения. Если изобразить функцию вектором длины , направленным вправо, то функция 2β аСos изобразится вектором длины 2β а (рис. 10.1), повернутым относительно вектора против часовой стрелки на угол , а функция - вектором длины , повернутым относительно вектора на угол . Чтобы уравнение (10.13) было удовлетворено, сумма трех перечисленных векторов должна совпадать с вектором, изображающим функцию f₀Cos t. Из рис. 10.1а видно, что такое совпадение возможно лишь при значении амплитуды а, которое определяется условием:

,

откуда

(10.14)

(заменили f₀ отношением F₀/m). Рис. 10.1а отвечает случаю   ω₀. Из рис. 10.1б, отвечающего случаю ω  ₀, получается такое же зна-чение а.

Рис. 10.1 позволяет получить также и значение , которое представляет собой величину отставания по фазе вынужденного колебания (10.10) от обусловившей его вынуждающей силы. Из рисунка 10.1а следует, что

. (10.15)

Подставив в (10.10) значения а и , определяемые формулами (10.14) и (10.15), получим функцию (10.9).

Функция (10.9) в сумме с (10.2) дает общее решение уравнения (10.1), описывающее поведение системы при вынужденных колебаниях. Слагаемое (10.2) играет заметную роль только в начальной стадии процесса, при так называемом установлении колебаний (рис. 10.2.) С течением времени из-за экспоненциального множителя е^{–β t} роль слагаемого (10.2) все больше уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (10.9).

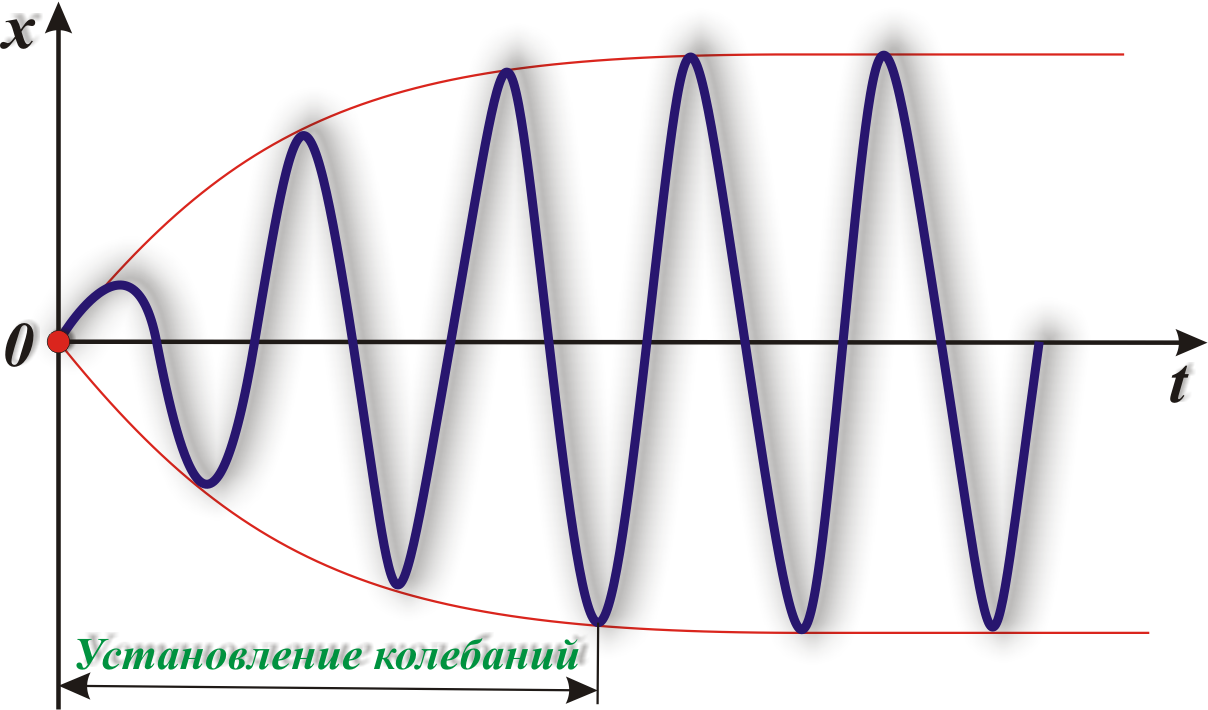
Рис. 10.2. Вынужденные колебания

Таким образом, функция (10.9) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (10.14) вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных ₀ и β) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания  также зависит от частоты вынуждающей силы (10.15).

10.3. Резонанс. Примеры резонансных явлений

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом, а соответствующая частота – резонансной частотой. При β²  ₀² значение _рез практически совпадает с собственной частотой ₀ колебательной системы.

Чтобы определить резонансную частоту _рез, нужно найти максимум функции (10.14) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по  и приравняв к нулю, мы получим условие, определяющее _рез:

. (10.16)

Уравнение (10.16) имеет три решения: ω=0 и . Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение:

. (10.17)

Подставив это значение частоты в (10.14), получим выражение для амплитуды при резонансе:

. (10.18)

Из (10.18) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность. Согласно (10.17) резонансная частота при тех же условиях (при β=0) совпадала с собственной частотой колебаний системы ₀.

Из формулы (10.18) вытекает, что при малом затухании (т.е. при β₀) амплитуда при резонансе приближенно равна

а_рез.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 10.3. Отдельные кривые на графике соответствуют различным значениям параметра β. В соответствии с (10.17) и (10.18), чем меньше β, тем выше и правее лежит максимум данной кривой. При очень большом затухании (таком, что ) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (рис.10.3 см. нижнюю кривую). Изображенная на рис. 10.3 совокупность графиков функции (10.14), соответствующих различным значениям параметра β, называется резонансными кривыми.

Анализируя резонансные кривые можно сделать следующие замечания. При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F₀. При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше β, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем "острее" получается максимум.

Рис. 10.3. Резонансные кривые

Резонанс играет очень большую роль в самых разнообразных явлениях, причем в одних – полезную, в других – вредную. Идя по доске, перекинутой через ров, можно попасть шагами в резонанс с собственным периодом системы (доски с человеком на ней), и доска начинает тогда сильно колебаться. То же самое может случиться и с мостом, по которому проходит войсковая часть или проезжает поезд (периодическая сила обусловливается ударами ног или ударами колес на стыках рельсов). Так, например, в 1906 г. в Петербурге обрушился так называемый Египетский мост через реку Фонтанку. Это произошло при переходе через мост кавалерийского эскадрона, причем четкий шаг лошадей, отлично обученных церемониальному маршу, попал в резонанс с частотой моста. Для предотвращения таких случаев войсковым частям при переходе через мосты приказывают обычно идти вольным шагом. Поезда же большей частью переезжают мосты на медленном ходу, чтобы период ударов колес о стыки рельсов был значительно больше периода собственных колебаний моста. Иногда применяют обратный способ, поезда проносятся через мосты на максимальной скорости.

Пароход также имеет собственный период качаний на воде. Если морские волны попадают в резонанс с периодом парохода, то качка становится особенно сильной. Капитан меняет тогда скорость парохода или его курс, и уходит от резонанса.

Неуравновешенность машин и двигателей является причиной того, что при работе этих машин возникает периодическая сила, действующая на опору машины – фундамент, корпус корабля и т.д. Период силы может совпасть при этом с собственным периодом опоры или, например, с периодом колебаний изгиба самого вращающегося вала или с периодом крутильных колебаний этого вала. Получается резонанс, колебания могут быть настолько сильны, что разрушают фундамент, ломают валы и т.д. Во всех таких случаях принимаются специальные меры, чтобы избежать резонанса (расстройка периодов, увеличение затухания и др.).

Очевидно, для того чтобы с помощью наименьшей периодической силы получить определенный размах вынужденных колебаний, нужно действовать в резонанс. Тяжелый язык колокола может раскачать даже не сильный человек, если он будет натягивать веревку с собственным периодом языка. Но самый сильный человек не раскачает колокол, дергая веревку не в резонанс.

Вместе с тем явление резонанса оказывается весьма полезным, особенно в акустике и радиотехнике. Резонанс позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора.