1.3. Скорость

Для характеристики движения материальной точки вводится векторная величина – скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени ей соответствует радиус-вектор (рис. 1.11). В течение малого промежутка времени ∆ точка пройдет путь ∆s и получит элементарное (бесконечно малое) перемещение .

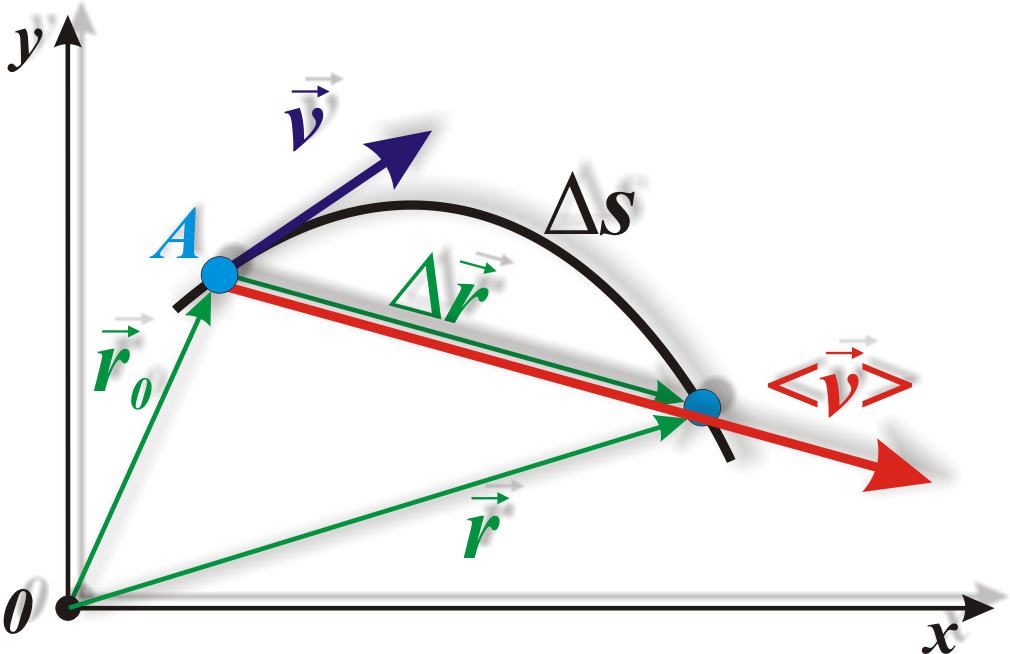
Рис. 1.11. Вектор скорости направлен по касательной

к траектории, вектор средней скорости <> направлен

по вектору перемещения

Вектором средней скорости <> называют отношение приращения радиус-вектора точки к промежутку времени ∆:

<>=. (1.3)

Направление вектора средней скорости совпадает с направлением . При неограниченном уменьшении ∆ средняя скорость стремится к предельному значению, которое называется мгновенной скоростью:

=. (1.4)

Мгновенная скорость, таким образом, есть векторная величина, равная первой производной радиуса вектора движущейся точки по времени. Вектор скорости направлен по касательной к траектории в сторону движения (рис. 1.11). По мере уменьшения ∆ путь ∆s все больше будет приближаться к ||, поэтому модуль мгновенной скорости равен

= || = , (1.5)

т.е. модуль мгновенной скорости равен первой производной пути по времени.

Используя единичные вектора , вектор можно разложить на три составляющие по осям прямоугольной декартовой системы координат:

=, (1.6)

причем, согласно (1.4) =, = , =

=. (1.7)

При описании плоского движения, когда траектория является плоской кривой, т.е. такой кривой, все точки которой лежат в одной плоскости, вектор скорости представляют в виде суммы двух составляющих (рис. 1.12):

= (1.8)

Рис. 1.12. Вектор представлен в виде

суммы двух составляющих: и

Первая составляющая равна:

. (1.9)

Она направлена вдоль радиус-вектора и характеризует быстроту изменения модуля

Вторая составляющая равна:

= r . (1.10)

Эта составляющая характеризует быстроту изменения радиусавектора по направлению, она связана с изменением угла

Векторы – единичные векторы.

Векторы и взаимно перпендикулярны. Следовательно,

= (1.11)

Если направление вектора скорости точки не изменяется, то траектория точки прямая линия, т.е. прямолинейное движение. В случае криволинейного движения точки направление ее скорости непрерывно изменяется.

При равномерном движении точки остается постоянной ее скорость , а путь, пройденный точкой за промежуток времени от до +∆, ∆s = ·∆. В этом случае, точка проходит за равные промежутки времени пути равной длины. Кинематическое уравнение можно записать и так s=s₀+v(t-t₀), где s₀ – путь в момент времени t_0.. Если точка движется равномерно и прямолинейно со скоростью вдоль оси , то зависимость ее координаты от времени имеет вид: , где  значение в начальный момент времени(=0), а − проекция скорости точки на ось .

Если модуль вектора скорости точки изменяется с течением времени, т. е =f() или просто (), то такое движение точки называется неравномерным. Неравномерное движение точки называется ускоренным, если в процессе движения модуль скорости точки увеличивается, т.е. () >0. Если () <0, то движение точки называется замедленным. Путь, пройденный материальной точкой за промежуток времени от до равен:

ds = (). (1.12)

Проинтегрировав по времени, найдем длину пути, пройденного точкой за промежуток времени от до :

S=. (1.13)

График зависимости от показан на рис. 1.13. Пройденный путь можно представить как площадь фигуры, ограниченной кривой (), осью и прямыми = и =.

Рис. 1.13. Путь, пройденный за время с момента

до момента , численно равен площади фигуры АВ

При стремлении всех к нулю ширина полосок убывает (одновременно число их растет), и ломаная линия в пределе сольется с кривой = (). Таким образом, путь, пройденный за время с момента до момента , численно равен площади, ограниченной графиком функции = (), осью времени и прямыми = и =.

Заметим, что среднее значение модуля скорости за время до равно

(1.14)

аналогично

< > =. (1.15)