8.2. Механические гармонические колебания

Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты Х от времени t задается уравнением, аналогичным уравнению (8.1):

. (8.7)

Согласно выражениям (8.4) и (8.5), скорость и ускорение колеблющейся точки соответственно равны

(8.8)

.

Сила , действующая на колеблющуюся материальную точку массой m, с учетом (8.7) и (8.8) равна

.

Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна

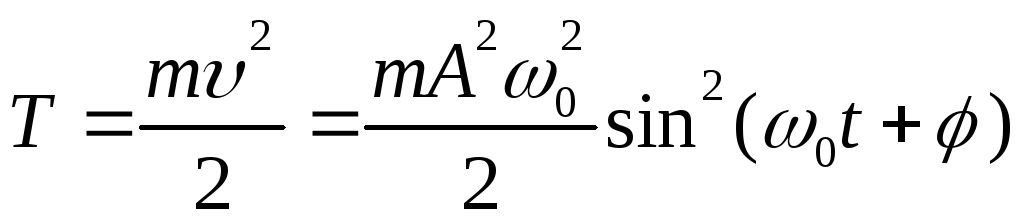(8.9)

или

. (8.10)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна

(8.11)

или

. (8.12)

Сложив (8.9) и (8.11), получим формулу для полной энергии:

. (8.13)

Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.

Из формул (8.10) и (8.12) следует, что Т и П изменяются с частотой 2, т.е. с частотой, которая в два раза превышает частоту гармонического колебания. На рис. 8.2 представлены графики зависимости Х, Т и П от времени. Поскольку , то из формул (8.9), (8.11) и (8.13) следует, что .

8.3. Гармонический осциллятор. Пружинный, математический

и физический маятники

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида:

.

Колебания гармонического осциллятора являются важным примером периодического движения и служат точкой или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, математический и физический маятники.

1. Пружинный маятник – это груз, массой m, подвешенной на абсолютно упругой пружине и совершающей гармонические колебания под действием упругой силы.

Рассмотрим систему, состоящую из шарика массы m, подвешенного на упругой пружине (рис. 8.3). В состоянии равновесия сила mg уравновешивается упругой силой :

. (8.14)

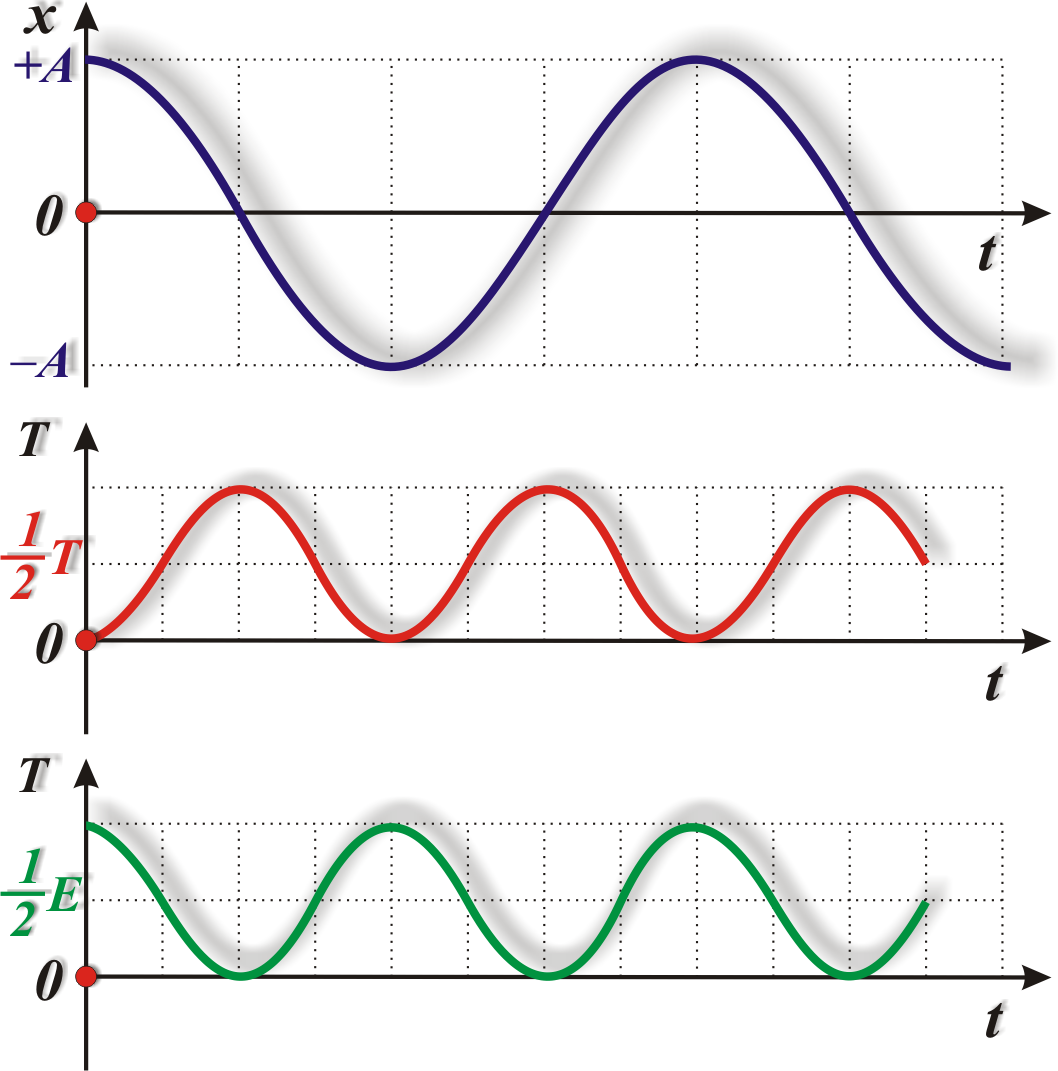
Рис. 8.2. Графики зависимости смещения, кинетической

и потенциальной энергии от времени при гармонических колебаниях

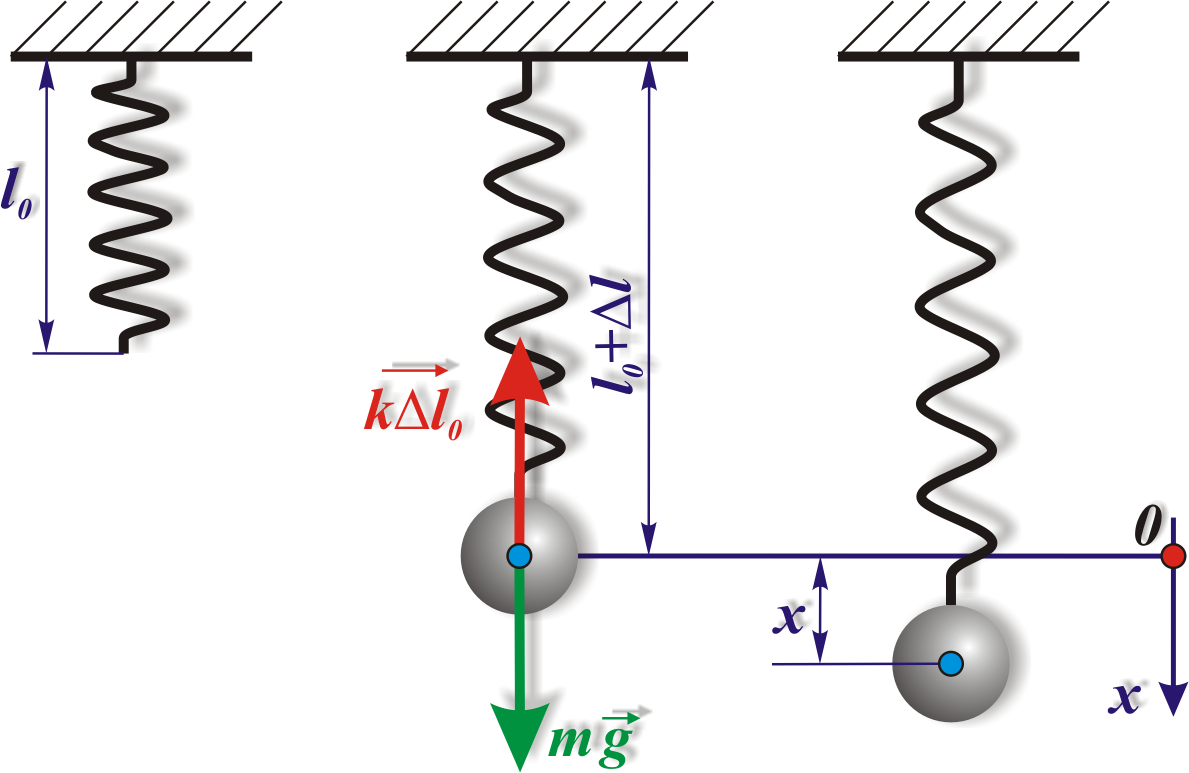
  Рис. 8.3. Пружинный маятник

Будем характеризовать смещение шарика из наложения равновесия координатой х, причем ось х направим по вертикали вниз, а нуль оси совместим с положением равновесия шарика.

Если сместить шарик от положения равновесия на расстояние, равное х, то удлинение пружины станет равным и проекция, результирующей силы на ось х (обозначим эту проекцию буквой f) примет значение

.

Учитывая условие равновесия (8.14), получим, что

. (8.15)

Знак «–» в формуле (8.15) отражает то обстоятельство, что смещение и сила имеют противоположные направления: если шарик смещен из положения равновесия вниз (х > 0), сила направлена вверх (f < 0), при смещении шарика вверх (х < 0), то сила направлена вниз (f > 0). Таким образом, сила f обладает следующими свойствами: 1) она пропорциональна смещению шарика из положения равновесия, 2) она всегда направлена к положению равновесия.

В рассмотренном примере сила (8.15) по своей природе упругая. Если сила не является по своей природе упругой, но подчиняется закону , то она называется квазиупругой силой.

Уравнение второго закона Ньютона для пружинного маятника имеет вид

или

. (8.16)

Уравнение (8.16) является дифференциальным уравнением колебаний пружинного маятника. Решение уравнения (8.16) можно записать в виде:

Обозначим в уравнении (8.16)

.

Учитывая формулу (8.2), период колебаний пружинного маятника:

. (8.17)

2. Математический маятник – это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

Отклоним маятник от положения равновесия угол a (рис. 8.4).

 

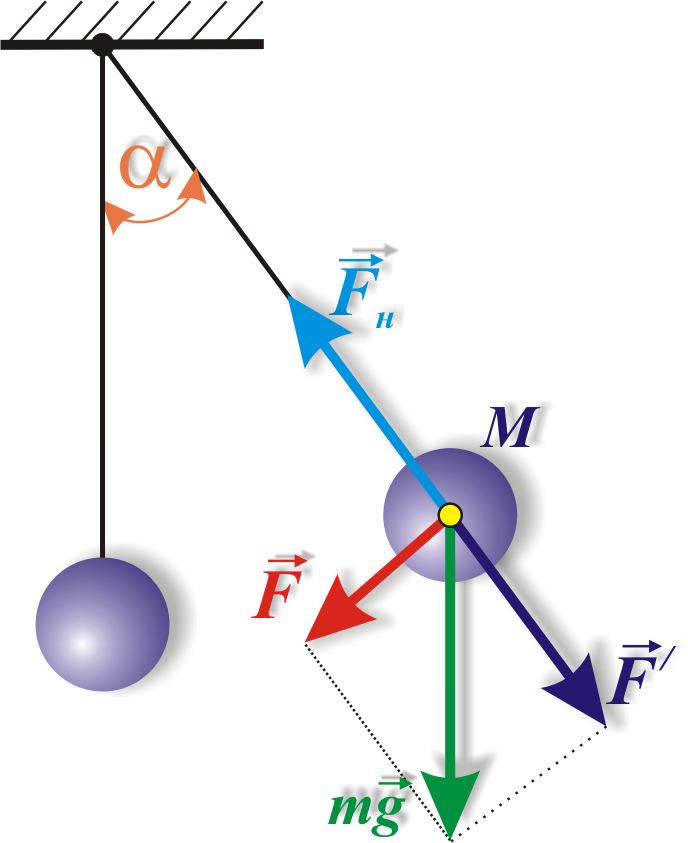
  Рис. 8.4. Математический маятник

 

Разложим мысленно силу тяжести mg, действующую на точку М, на две составляющие F^/ и F, направленные соответственно вдоль нити и перпендикулярно к ней. Сила F^/ = mgcosa будет растягивать нить и уравновесится натяжением нити F_н. Неуравновешенной останется составляющая силы F = mg sin a. Таким образом, на точку М всегда будет действовать две силы mg и F_н, направленные под углом (p – a) друг к другу. Равнодействующей этих сил по правилу параллелограмма будет сила F = mg sin a, направленная по касательной к дуге ОМ в сторону точки О. Когда груз придет в наинизшее положение, т.е. в т. О, силы mg и F_н полностью уравновесятся. Таким образом, точка О есть положение равновесия груза m. Обозначим отрезок дуги ОМ, характеризующий путь, пройденный точкой М из положения равновесия, через х и будем считать угол a и величину х положительными при отклонении нити с грузом вправо от вертикали и отрицательными – при отклонении влево. Угол a, измеряемый в радианах, численно равен отношению длины дуги х, на которую он опирается, к радиусу окружности l. Тогда (с учетом направления) сила F, действующая на точку М, может быть выражена в виде

. (8.18)

Для малых углов отклонения от вертикали, не превышающих 5-6° с достаточной степенью точности можно заменить sina углом a (в радианах). Тогда сила, действующая на точку М, будет равна

. (8.19)

Обозначим , тогда получим . Видим, что результирующая сила F, действующая на математический маятник, находящийся в поле земного тяготения меняется подобно упругой силе, по своей природе она не является упругой и называется квазиупругой.

По второму закону Ньютона:

. (8.20)

Из (8.19) и (8.20) получаем:

или

. (8.21)

Уравнение (8.21) является дифференциальным уравнением колебаний математического маятника.

Решение (8.21) можно записать в виде:

Обозначим в уравнении (8.21)

. (8.22)

Учитывая, что

. (8.23)

Период колебаний математического маятника равен:

. (8.24)

Из формулы (8.24) видно, что период колебаний математического маятника не зависит от амплитуды (при малых углах) и не зависит от массы маятника.

3. Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, проходящей через точку О, несовпадающей с центром масс тела (рис. 8.5).

Если маятник отклонен из положения равновесия на некоторый угол a, то в соответствии с уравнением динамики вращательного движения твердого тела, момент М возвращающей силы можно записать в виде

, (8.25)

где I₀ – момент инерции маятника относительно оси, проходящей через точку подвеса О.

С другой стороны момент силы M определяется

, (8.26)

т.к. (соответствует малым колебаниям маятника), получим:

. (8.27)

  Рис. 8.5. Физический маятник

 

Вращательный момент имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому моменту М и угловому смещению j нужно приписывать противоположные знаки

. (8.28)

Угловое ускорение равно:

. (8.29)

Подставив (8.29) в (8.25) и учитывая (8.28) получим:

. (8.30)

После преобразований получим:

. (8.31)

Уравнение (8.31) является дифференциальным уравнением колебаний физического маятника.

Решение уравнения (8.31) можно записать в виде:

Обозначим в уравнении (8.31)

. (8.32)

Учитывая, что , найдем период колебаний физического маятника, как:

. (8.33)

В уравнении (8.33) обозначим

, (8.34)

которая называется приведенной длиной физического маятника.

Точка О^/ на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качания физического маятника (рис. 8.5). Применяя теорему Штейнера, получим

,

т.е. ОО^/ всегда больше ОС. Точка подвеса О маятника и центр качаний О^/ обладают свойством взаимозаменяемости. Если точку подвеса перенести в центр качаний, то прежняя точка О подвеса станет новым центром качаний, и период колебаний физического маятника не изменится.