7.7.3. Связь между энергией и импульсом частицы

Энергия Е и импульс р частицы имеют различные значения в разных системах отсчета. Однако существует величина – некоторая комбинация Е и р, которая является инвариантной, т.е. имеет одно и то же значение в разных системах отсчета. Эта величина есть . Покажем это.

Воспользовавшись формулами и запишем

.

Величина не зависит от скорости частицы, а следовательно, и от системы отсчета. Другими словами, величина действительно является инвариантом и имеет одно и то же значение во всех инерциальных системах отсчета.

Этот вывод во многих случаях позволяет упростить анализ и решение различных вопросов.

Приведем еще два полезных соотношения, с которыми приходится часто встречаться. Первое:

(7.31)

и второе – связь между импульсом и кинетической энергией Т час-тицы

. (7.32)

Последнее соотношение при переходит в ньютоновское: , а при приобретает вид .

Рассмотрим вопрос о существовании частиц с нулевой массой покоя (m₀=0). Из формул

,

следует, что частица с массой покоя m₀=0 может иметь энергию и импульс только в том случае, если она движется со скоростью света с. При этом обе последние формулы принимают вид 0/0. Однако это не означает неопределенности энергии и импульса такой частицы. Обе эти величины, оказывается, не зависят от скорости, причем связь между импульсом р и энергией Е дается формулой (7.31), где , т.е.

.

Таким образом, согласно теории относительности, существование частиц с нулевой массой покоя возможно, причем эти частицы могут двигаться только со скоростью с. Это движение – единственное состояние, в котором такие частицы могут существовать. Остановка подобной частицы равносильна ее поглощению (исчезновению). Такими частицами являются фотон и нейтрино.

Глава 8. Свободные гармонические колебания

 

8.1. Гармонические колебания и их характеристика

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы хорошо распространены в природе и технике, например, качение маятника часов и т.д.

В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. В данной главе рассматриваются механические колебания.

В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания. В данной главе рассматриваются свободные колебания.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Гармонические колебания величины х описываются уравнением типа

(8.1)

где А – максимальное значение колеблющейся величины, называемой амплитудой колебания; - круговая (циклическая) частота; - начальная фаза колебания в момент времени t = 0; - фаза колебания в момент времени t.

Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так косинус изменяется в пределах от +1 до –1, то х может принимать значения от +А до – А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2p, т.е.

.

Откуда

. (8.2)

Величина, обратная периоду колебаний,

, (8.3)

т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (8.2) и (8.3), получим

.

Циклическая (круговая) частота равна числу полных колебаний, совершающихся за 2p секунд. Единица частоты Герц (Гц): 1 Гц – частота периодического процесса, при которой за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины х:

, (8.4)

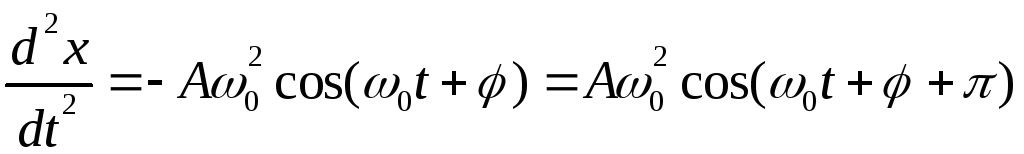, (8.5)

т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды величины (8.4) и (8.5) соответственно равны и . Фаза величины (8.4) отличается от фазы величины (8.1) на , а фаза величины (8.5) отличается от фазы величины (8.1) на . Следовательно, в момент времени, когда х = 0, приобретает наибольшие значения; когда же х достигает максимально отрицательного значения, то приобретает наибольшее положительное значение (рис. 8.1).

 

Рис. 8.1. Графики зависимости смещения, скорости

и ускорения от времени при гармонических колебаниях

 

Из выражения (8.5) следует дифференциальное уравнение гармонических колебаний

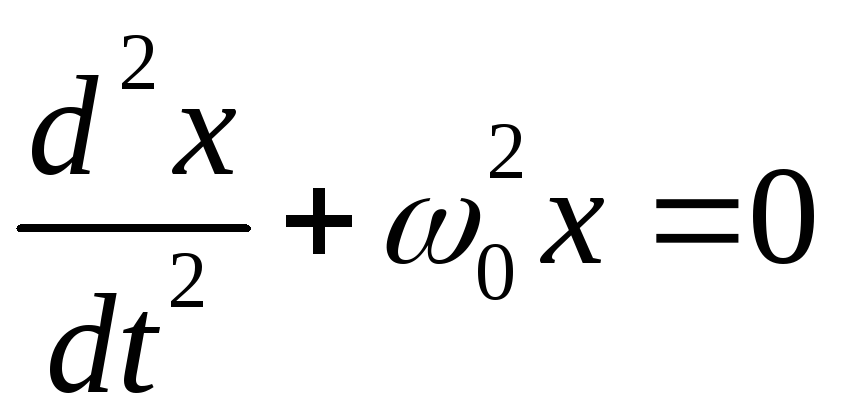, (8.6)

где .

Решением этого уравнения является выражение (8.1).