
- •Механика
- •Механика
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Кинематика
- •Механическое движение
- •1.2. Некоторые сведения о векторах
- •1.3. Скорость
- •1.4. Ускорение
- •1.5. Угловая скорость и угловое ускорение
- •Глава 2. Динамика материальной точки
- •2.1. Первый закон Ньютона. Инерциальные системы отсчета
- •2.2. Второй закон Ньютона
- •2.3. Третий закон Ньютона
- •2.4. Сила. Силы трения
- •2.5. Импульс. Закон сохранения импульса
- •2.6. Центр масс. Движение тела переменной массы
- •Глава 3. Работа и энергия
- •3.1. Понятие о работе и энергии. Мощность. Консервативные
- •Кинетическая энергия
- •Потенциальная энергия
- •Закон сохранения механической энергии
- •Графическое представление энергии.
- •3.6. Применение законов сохранения энергии и импульса
- •Используя (3.32), получаем
- •Движение в центральном поле сил
- •Глава 4. Механика твердого тела
- •4.1. Движение твердого тела
- •4.2. Момент силы
- •4.3. Центр масс твердого тела и его движение
- •4.4. Момент импульса и закон его сохранения
- •4.5. Основное уравнение динамики вращательного движения
- •4.6. Момент инерции
- •4.7. Кинетическая энергия твердого тела
- •4.7.1. Вращение тела вокруг неподвижной оси
- •4.7.2. Работа внешних сил при вращении твердого тела
- •4.7.3. Кинетическая энергия тела при плоском движении
- •Глава 5. Тяготение. Неинерциальные системы
- •5.1. Развитие представлений о природе тяготения
- •5.2. Законы Кеплера. Закон всемирного тяготения
- •5.3. Гравитационное поле и его характеристики
- •5.4. Сила тяжести и вес. Невесомость
- •5.5. Космические скорости
- •5.6. Неинерциальные системы отсчета. Силы инерции
- •5.6.1. Силы инерции при ускоренном поступательном
- •5.6.2. Центробежная сила инерции
- •5.6.3. Сила Кориолиса
- •Глава 6. Элементы механики сплошных сред
- •6.1. Гидроаэростатика
- •6.1.1. Давление
- •6.1.2. Распределение давления в покоящихся жидкости и газе
- •6.1.3. Выталкивающая сила
- •6.2. Гидроаэродинамика
- •6.2.1. Линии и трубки тока. Неразрывность струи
- •6.2.2. Уравнение Бернулли
- •6.2.3. Измерение давления в текущей жидкости
- •6.2.4. Применение к движению жидкости закона сохранения
- •6.2.5. Силы внутреннего трения
- •6.2.6. Ламинарное и турбулентное течение
- •6.2.7. Движение тел в жидкостях и газах
- •6.2.8. Подъемная сила
- •Глава 7. Элементы специальной теории
- •7.1. Принцип относительности Галилея.
- •7.2. Постулаты специальной теории относительности
- •7.3. Преобразования Лоренца
- •7.4. Следствия из преобразований Лоренца
- •7.4.1. Одновременность событий в разных системах отсчета
- •7.4.2. Длительность событий в разных системах отсчета
- •7.4.3. Длина тел в разных системах отсчета
- •7.4.4. Релятивистский закон сложения скоростей
- •7.5. Интервал между событиями
- •7.6. Релятивистская динамика. Релятивистский импульс
- •7.7. Закон взаимосвязи массы и энергии
- •7.7.1. Кинетическая энергия релятивистской частицы
- •7.7.2. Закон взаимосвязи массы и энергии
- •7.7.3. Связь между энергией и импульсом частицы
- •Глава 8. Свободные гармонические колебания
- •8.1. Гармонические колебания и их характеристика
- •8.2. Механические гармонические колебания
- •8.3. Гармонический осциллятор. Пружинный, математический
- •8.4. Графическое изображение гармонических колебаний.
- •8.5. Сложение колебаний одинакового направления
- •8.6. Сложение взаимно перпендикулярных колебаний
- •Глава 9. Свободные Затухающие колебания
- •9.1. Дифференциальное уравнение свободных затухающих
- •9.2. Основные характеристики затухающих колебаний
- •Глава 10. Вынужденные колебания
- •10.1. Дифференциальное уравнение вынужденных колебаний
- •10.2. Решение дифференциального уравнения вынужденных
- •10.3. Резонанс. Примеры резонансных явлений
- •Глава 11. Волны в упругой среде
- •11.1. Упругие волны
- •11.2. Уравнение плоской и сферической волн
- •11.3. Уравнение плоской волны, распространяющейся
- •11.4. Волновое уравнение
- •11.5. Скорость распространения упругих волн
- •11.6. Энергия упругой волны
- •11.6.1. Плотность энергии упругой волны
- •11.6.2. Плотность потока энергии
- •11.7. Стоячие волны
- •11.7.1. Уравнение стоячей волны
- •11.7.2. Энергия стоячей волны
- •11.8. Эффект Доплера для звуковых волн
- •Литература
- •Механика
- •302020, Г. Орел, Наугорское шоссе, 29.
7.4. Следствия из преобразований Лоренца
7.4.1. Одновременность событий в разных системах отсчета
Пусть
в системе К
в точках с координатами x1
и x2
в моменты времени t1
и t2
происходят два события. В системе К/
им соответствуют координаты
![]() и
и
![]() и моменты времени
и моменты времени
![]() и
и
![]() .
Если эти события в системе К
происходят в одной точке (
.
Если эти события в системе К
происходят в одной точке (![]() )
и являются одновременными (
)
и являются одновременными (![]() ),
то, согласно преобразованиям Лоренца
(7.12),
),
то, согласно преобразованиям Лоренца
(7.12),
![]() ,
,
![]() ,
,
т.е. эти события являются одновременными и совпадают в пространстве для любой инерциальной системы отсчета.
Если
события в системе К
пространственно разобщены (![]() ),
но одновременны (
),
но одновременны (![]() ),
то в системе К/
им будут соответствовать координаты
),
то в системе К/
им будут соответствовать координаты
 ,
,

и моменты времени
 ,
,

![]() ,
,
![]() .
.
Таким
образом, в системе К/
эти события, оставаясь пространственно
разобщенными, оказываются и неодновременными.
Знак разности
![]() определяется знаком выражения
определяется знаком выражения
![]() ,
поэтому в различных точках системы
отсчета К/
(при разных v)
разность
,
поэтому в различных точках системы
отсчета К/
(при разных v)
разность
![]() будет различной по величине и может
отличаться по знаку. Поэтому в одних
системах отсчета первое событие может
предшествовать второму, в то время как
в других системах отсчета, наоборот,
второе событие предшествует первому.
Это не относится к причинно-следственным
событиям, т.к. можно показать, что порядок
следования причинно-следственных
событий одинаков во всех инерциальных
системах отсчета.
будет различной по величине и может
отличаться по знаку. Поэтому в одних
системах отсчета первое событие может
предшествовать второму, в то время как
в других системах отсчета, наоборот,
второе событие предшествует первому.
Это не относится к причинно-следственным
событиям, т.к. можно показать, что порядок
следования причинно-следственных
событий одинаков во всех инерциальных
системах отсчета.
7.4.2. Длительность событий в разных системах отсчета
Пусть
в некоторой точке (с координатой x),
покоящейся относительно системы К,
происходит событие, длительность
которого
![]() ,
где t1
и t2
– моменты времени начала и конца события
соответственно. Длительность этого же
события в системе К/
,
где t1
и t2
– моменты времени начала и конца события
соответственно. Длительность этого же
события в системе К/
![]() ,
,
причем началу и концу события соответствуют моменты времени
 ,
,
 .
.
Длительность события в системе К/
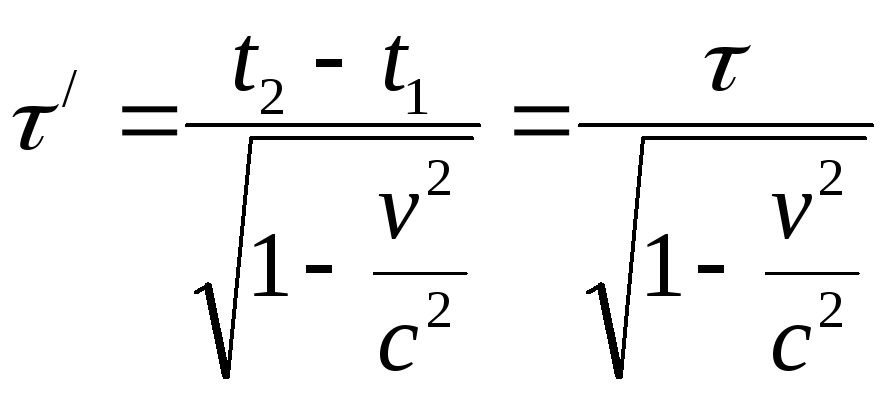 .
(7.13)
.
(7.13)
Из
соотношения (7.13) видно, что
![]() ,
т.е. длительность события, происходящего
в некоторой точке, наименьшая в той
инерциальной системе отсчета, относительно
которой эта точка неподвижна. Иначе
говоря, интервал времени
,
т.е. длительность события, происходящего
в некоторой точке, наименьшая в той
инерциальной системе отсчета, относительно
которой эта точка неподвижна. Иначе
говоря, интервал времени
![]() ,
отсчитанный по часам в системе К/,
с точки зрения наблюдателя в системе
К,
больше интервала
,
отсчитанный по часам в системе К/,
с точки зрения наблюдателя в системе
К,
больше интервала
![]() ,
отсчитанного по его часам. А именно
часы, движущиеся относительно инерциальной
системы отсчета, идут медленнее покоящихся
часов – ход часов замедляется в системе
отсчета, относительно которой часы
движутся. Из (7.13) следует, что замедление
хода часов заметно лишь при скоростях,
близких к скорости света в вакууме.
,
отсчитанного по его часам. А именно
часы, движущиеся относительно инерциальной
системы отсчета, идут медленнее покоящихся
часов – ход часов замедляется в системе
отсчета, относительно которой часы
движутся. Из (7.13) следует, что замедление
хода часов заметно лишь при скоростях,
близких к скорости света в вакууме.
7.4.3. Длина тел в разных системах отсчета
Рассмотрим
стержень, расположенный вдоль оси x
и покоящийся относительно системы К/.
Длина стержня в этой системе отсчета
равна
![]() ,
где
,
где
![]() и
и
![]() – не изменяющиеся со временем
– не изменяющиеся со временем
![]() координаты концов стержня в системе
К/.
Относительно системы К
стержень движется со скоростью v.
Найдем длину стержня в этой системе
отсчета. Для этого отметим координаты
концов стержня x1
и x2
в один и тот же момент времени t1
= t2
= t.
Разность
координаты концов стержня в системе
К/.
Относительно системы К
стержень движется со скоростью v.
Найдем длину стержня в этой системе
отсчета. Для этого отметим координаты
концов стержня x1
и x2
в один и тот же момент времени t1
= t2
= t.
Разность
![]() даст искомую длину. Используя формулы
преобразований Лоренца, можно записать
даст искомую длину. Используя формулы
преобразований Лоренца, можно записать
 ,
,
 ,
,
откуда
 ,
,
![]() ,
(7.14)
,
(7.14)
т.е. длина стержня l, измеренная в системе, относительно которой он движется, оказывается меньше длины l0, измеренной в системе, относительно которой стержень покоится.
Заметим, что в направлении осей у и z размеры стержня одинаковы во всех системах отсчета.
Из (7.14) видим, что размеры движущихся тел в направлении движения сокращаются тем больше, чем больше скорость движения. Это явление называется лоренцевым сокращением.
