1.2. Некоторые сведения о векторах
В физике для описания движения используют скалярные (путь, время, масса и др.) и векторные (скорость, ускорение, сила, импульс и др.) величины.
Величины, для задания которых достаточно одного численного значения, называются скалярными. Величины, характеризующие численным значением и направлением, называются векторными. Для векторной величины необходимо знать точку приложения, направление и модуль. Вектор изображается в виде стрелки, начало которой в точке приложения, направление совпадает с направлением вектора, а длина стрелки в выбранном масштабе определяется модулем вектора.
Векторы, направленные вдоль параллельных прямых (в одну и ту же или в противоположные стороны), называют коллинеарными. Векторы, которые лежат в параллельных плоскостях, называют компланарными.
Сложение
и вычитание векторов.
Сложение
векторов производится по правилу
параллелограмма, результирующий вектор
его диагональ (рис. 1.4). Модуль вектора
находим через модули векторов |
|,
|
|
и угол между ними
на основе теоремы косинусов.
Рис.
1.4.
При сложении
двух векторов
и
результирующий
вектор
изображается диагональю параллелограмма,
сторонами
которого служат векторы
и
Сложение векторов удобно проводить без построения параллелограмма. Начало второго вектора совместить с концом первого, а затем провести из начала первого в конец второго результирующий вектор (рис. 1.5). Этими способами можно сложить любое число векторов.
Рис. 1.5. Сложение нескольких векторов
Разностью
двух векторов
и
называется вектор
,
который в сумме с вектором
дает вектор
(рис. 1.6).
Рис.
1.6.
Разность
двух векторов
причем
Умножение
вектора на скаляр.
В результате умножения вектора
на скаляр
получается новый вектор
,
модуль которого в α
раз больше модуля вектора
,
а направление совпадает с направлением
вектора
,
если α
>0, и противоположно ему, если α<0.
Деление вектора на скаляр
равносильно умножению вектора на скаляр
α
=
.
Из
определения операции умножения вектора
на скаляр следует, что всякий вектор
можно представить в виде
,
где
модуль вектора
,
− вектор, модуль которого равен единице,
имеющий такое же направление, как и
вектор
.
Вектор
называют единичным вектором или ортом
вектора
.
Орт можно представить в виде
=
/
.
Проекция
вектора.
Рассмотрим некоторое направление в
пространстве, которое зададим осью
.
Пусть вектор
образует с осью
угол
Величину
=
,
где
- модуль вектора
,
называют проекцией вектора
на ось
(рис. 1.7).
Проекция
есть величина алгебраическая. Если
вектор образует с данным направлением
острый угол, то
>0,
и проекция положительна. Если угол
тупой, то проекция отрицательна.
Рис.
1.7.
Проекция
вектора
на ось
−
=
Если
прямая, вдоль которой направлен вектор
и ось
не пересекаются, то для определения
угла
нужно взять прямую параллельную вектору
.
Угол между этой прямой и осью
и будет интересующий нас угол
.
Радиус-вектор.
Радиусом – вектором
некоторой точки М
называется вектор, проведенный из начала
координат в данную точку
(рис. 1.8). Его
проекции на координатные оси равны
декартовым координатам данной точки:
.
Используя единичные векторы
можно записать:
Для квадрата модуля радиуса-вектора
тогда имеем
.
Рис.
1.8.
Радиус-вектор
точки М −
Умножение вектора на вектор. Различают скалярное и векторное произведение векторов. Результатом скалярного произведения является скаляр, результатом векторного произведения является вектор. Отметим, что операции деления вектора на вектор не существует.
Скалярное
произведение
двух векторов
и
называют скаляр, численно равный
произведению модулей векторов на косинус
угла между ними:
=|
||
|
или
=|
||
|
(рис.1.9). Можно также сказать, что скалярное
произведение двух векторов называется
скаляр, равный произведению модуля
одного из перемножаемых векторов на
проекцию второго вектора на направление
первого, т.е.
=
b|
|=|
|
a.
Из определения следует, что скалярное
произведение коммутативно, т.е. не
зависит от порядка сомножителей
=
.
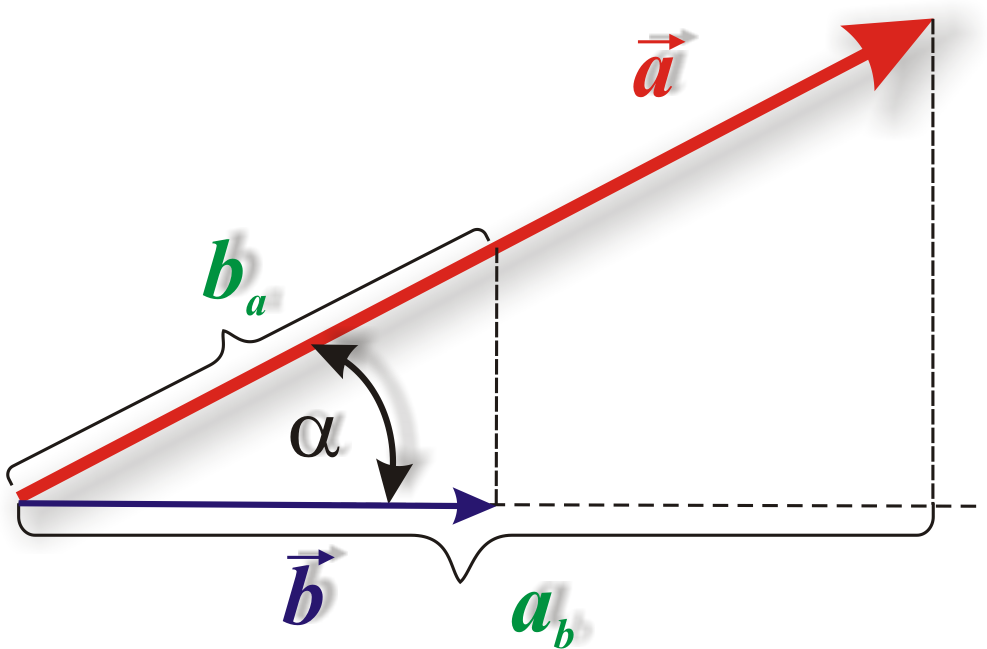
Рис. 1.9. Скалярное произведение
двух
векторов
=
=
b|
|=|
|
a
Скалярное
произведение векторов дистрибутивно:
произведение вектора
на сумму нескольких векторов равно
сумме произведений вектора
на каждый из складываемых векторов,
взятый в отдель-ности:
(
.
Векторным
произведением
векторов
и
называют вектор
определяемый как
=
|
||
|
=
,
где
и
– модули перемножаемых векторов,
-
угол между векторами,
− единичный вектор нормали к плоскости,
в которой лежат векторы
и
(рис. 1.10). Направление
выбирается так, чтобы последовательность
векторов
,
,
образовывала
правовинтовую систему (правило правого
винта).
Это означает, что если смотреть вслед
вектору
то совершаемый по кратчайшему пути
поворот от первого сомножителя ко
второму осуществляется по часовой
стрелке. На рис 1.10 вектор
направлен «от нас» и поэтому изображается
кружком с крестиком. Направление вектора
совпадает с вектором
.
Рис.
1.10.
Векторное
произведение векторов
и
есть вектор
=
[
]
=
Символически
векторное произведение можно записать
двумя способами [
∙
],
.
При рассмотрении таких векторов, как
радиус – вектор, сила, скорость и т.п.
вопрос о выборе направления векторов
не возникает – оно вытекает естественным
образом из природы самих величин.
Подобные векторы называются истинными
(или полярными). Векторы типа [
],
направление которых связывается с
направлением вращения, называют
псевдовекторами (или аксиальными
векторами). При изменении условия,
например, при переходе от правой системы
координат к левой, направления
псевдовекторов изменяются на обратные,
истинные же векторы при этом остаются
без изменений. Векторное произведение
будет псевдовектором только в случае,
когда оба перемножаемых вектора являются
истинными (или оба – псевдовекторы).
Векторное же произведение истинного
вектора на псевдовектор будет истинным
вектором. Векторное произведение не
обладает свойством коммутативности:
[
]
= − [
].